学习笔记|残差|检验多重共线性|线性回归分析|德宾沃森检验|方差分析（ANOVA）|回归系数|残差和预测值|规范表达|《小白爱上SPSS》课程：SPSS第二十一讲：多元线性回归分析（超级详细）

学习目的

SPSS第二十一讲：多元线性回归分析（超级详细）

软件版本

IBM SPSS Statistics 26。

原始文档

《小白爱上SPSS》课程
#统计原理

多元线性回归分析

今天我们来学习多元线性回归分析，它用来评价一个因变量和多个自变量之间关系的统计方法。除了需要满足一元线性回归的条件之外，多元线性回归还需要满足【多个自变量不存在多重共线】的条件.
多元线性回归需要满足如下条件:
（1）自变量和因变量在理论上有因果关系；
（2）因变量为连续型变量；
（3）各自变量与因变量之间存有线性关系；
（4）残差要满足正态性、独立性、方差齐性。
（5）多个自变量不存在多重共线性
其中，线性（Linear）、正态性（Normal）、独立性（independence）、方差齐性（Equal Variance），俗称LINE，是线性回归分析的四大基本前提条件。
这里稍微解释它们概念：
Q1 线性：解释自变量X和因变量Y必须要有线性关系吗？
—不是！只有当X是连续型数据或者等级数据（不设哑变量）时，才要求X与Y有线性的关系。当X是二分类或无序多分类，没有线性条件的要求。
Q2独立性：要求因变量Y各观察值相互独立吗？
—不是，是要求残差是独立的。
Q3正态性：要求因变量Y各观察值正态分布吗？
—不是，是要求残差正态分布。
Q4方差齐性：要求不同的解释变量X时，因变量Y方差相等吗？
—没错，但是对于多元线性回归分析，更加合理的理解是在不同Y预测值情况下，残差的方差变化不大。
Q5：一定要严格满足LINK吗？
—如果回归分析只是建立自变量与因变量之间关系，无须根据自变量预测因变量的容许区间和可信度等，则方差齐性和正态性可以适当放宽。

何为残差？

残差在数理统计中是指实际观察值与估计值（拟合值）之间的差。我们以一元线性回归为例，它只有一个自变量，其模型可以表示为：

上述公式是基于样本得到的结果，b0和b1均为统计量。
若该公式拓展到总体人群，则为：

值得注意的是，这里x是真实的变量值x，而y带了一顶帽子，并非是y的真实值，而是成为y的预测值或者估计值。实际上，x和y没有严格上一一对应的关系，通过x产生的预测值，是接近于y但不等于y。
y预测值与y真实值之间的差值我们称之为残差。
残差反映了除了x和y之间的线性关系之外的随机因素对y的影响，是不能由x和y之间的线性关系所解释的变异性。
可以这么来理解ϵ：我们对y的预测是不可能达到与真实值完全一样的，因此必然会产生误差，我们就用ϵ来表示这个无法预测的误差。我们通过引入了ϵ可以让模型达到完美状态，也就是理论的回归模型。
结合残差，真实的y和x关系如下：
同样的，多个自变量存在的情况下，多重线性回归模型的表示如下：
其中，bk、βk：回归系数，在多重线性回归中，被称之为偏回归系数，表示每个自变量都对y部分的产生了影响。
意义与简单线性回归结果相似，反映的是x对y的影响力，是当x每改变一个观测单位时所引起y的改变量。
这里e是样本的预测值与测量值的差别，ϵ是总体中预测值与真实值的差别。戴了帽子的y预测值的变异性是解释变量x们能够预测和解释的。
一般情况下，成功的线性回归模型实现：
（1）残差ϵ是一个期望为0的随机变量，即E(ϵ)=0
（2）对于预测值的所有值，ϵ的方差σ^2都相同
（3）残差ϵ是一个服从正态分布的随机变量，且相互独立，即ϵ~N(0,σ^2)

何为多重共线？

当2个或多个自变量高度相关时，就会出现多重共线。它不仅影响自变量对因变量变异的解释能力，还影响整个多重线性回归模型的拟合。

一、实战案例

小白研究运动员训练比赛满意感与成就感降低、情绪体力耗竭、运动负评价、自尊等变量之间关系，试建立多元线性回归方程。
读数据：

GET 
  FILE='E:\E盘备份\recent\小白爱上SPSS\小白数据\第二十一讲：自尊、心理疲劳对训练满意感的预测.sav'. 

该案例研究运动员训练比赛满意感与多个自变量（成就感降低、情绪体力耗竭、运动负评价、自尊）之间的关系。从专业知识上可认为成就感降低、情绪体力耗竭、运动负评价、自尊是可以预测训练比赛满意感的。

二、统计策略

统计分析策略口诀“目的引导设计，变量确定方法”。
针对上述案例，扪心五问。
Q1：本案例研究目的是什么？
A：关联研究，探讨多个自变量与因变量之间的因果关系。
Q2：分析的组数是多少呢？
A：五组数据。
Q3：本案例属于什么研究设计？
A：调查研究
Q4：有几个变量？
A：有五个变量。分别是成就感降低、情绪体力耗竭、运动负评价、训练比赛满意感、自尊。
（训练比赛满意感为因变量，成就感降低、情绪体力耗竭、运动负评价、自尊为自变量）
Q5：残差是否具有独立性、方差齐性和正态分布？
A：需要检验残差是否满足独立性、方差齐性和正态性。
Q6：各自变量之间是否存在多重共线性？
A: 需要检验
概括而言，如果数据满足以下条件，则采用多元线性回归分析。

三、SPSS操作

（一）绘制散点图

对于线性关系的条件，一般要求当x是连续型变量或者等级变量时，需绘制散点图探讨与y是否存在着线性趋势的关系；如x为二分类或者无序多分类，无须绘制散点图。
本例绘制成就感降低、情绪体力耗竭、运动负评价、自尊与训练比赛满意感之间关系的散点图分析。具体操作如下。
Step1：图形—图形画板模板选择器；
Step2：按Shift选择左边的对话框所有的变量，同时点击【散点图矩阵】，点击【确定】。

命令行：

GGRAPH 
  /GRAPHDATASET NAME="graphdataset" 
    VARIABLES=训练比赛满意感[LEVEL=scale] 运动负评价[LEVEL=scale] 自尊[LEVEL=scale] 情绪体力耗竭[LEVEL=scale] 
    成就感降低[LEVEL=scale] 
    MISSING=LISTWISE REPORTMISSING=NO 
  /GRAPHSPEC SOURCE=VIZTEMPLATE(NAME="Scatterplot Matrix (SPLOM)"[LOCATION=LOCAL] 
    MAPPING( "all"="成就感降低"[DATASET="graphdataset"] "all"="情绪体力耗竭"[DATASET="graphdataset"] 
    "all"="运动负评价"[DATASET="graphdataset"] "all"="自尊"[DATASET="graphdataset"] 
    "all"="训练比赛满意感"[DATASET="graphdataset"])) 
    VIZSTYLESHEET="Traditional"[LOCATION=LOCAL] 
    LABEL='散点图矩阵 (SPLOM): 自尊-运动负评价-成就感降低-训练比赛满意感-情绪体力耗竭' 
    DEFAULTTEMPLATE=NO.

输出结果如下，重点关注最后一行，即各自变量（成就感降低、情绪体力耗竭、运动负评价、自尊）与因变量（训练比赛满意感）之间线性关系。从图中可知，各自变量与因变量之间存有线性关系。

（二）线性回归分析操作

Step1:依次点击“分析——回归——线性;
Step2: 将“训练比赛满意感”纳入“因变量”；将成就感降低、情绪体力耗竭、运动负评价、自尊放入“自变量”；方法选择“输入”;
Step3: 点击“统计” 默认选项“估算值”；“模型拟合”；另选择“durin waston(德宾-沃森)、共线性诊断和“描述”。设置完后，点击“继续”。

Step4 : 在弹出“线性回归：图”对话框中将 “*ZRESID”（标准化残差）放入Y轴中，将“*ZPRED”（标准化预测值）放入X轴中，勾选“直方图”和“正态概率图”，单击“继续”。点击“确定”。
Step5: 点击“保存”后勾选预测值的“未标准化”和“残差的未标准化”。
命令行：

REGRESSION 
  /DESCRIPTIVES MEAN STDDEV CORR SIG N 
  /MISSING LISTWISE 
  /STATISTICS COEFF OUTS R ANOVA COLLIN TOL /*COLLIN TOL：共线性诊断*/
  /CRITERIA=PIN(.05) POUT(.10) 
  /NOORIGIN 
  /DEPENDENT 训练比赛满意感 /*“因变量”*/
  /METHOD=ENTER 成就感降低 情绪体力耗竭 运动负评价 自尊 /*“自变量”*/
  /SCATTERPLOT=(*ZRESID ,*ZPRED) 	/*Y轴：*ZRESID”（标准化残差），X轴：*ZPRED”（标准化预测值）*/
  /RESIDUALS DURBIN HISTOGRAM(ZRESID) NORMPROB(ZRESID)	 /*德宾残差（默认值），直方图、正态概率图*/
  /SAVE PRED RESID	/*“保存”预测值的“未标准化”和残差的“未标准化”*/.

四、结果解读

第一，R方结果和残差独立性检验（德宾沃森检验）

模型摘要是判断两者之间线性关系的重要指标，也反映了回归的拟合程度。

①一般情况下，R²看的是“调整R²”，该值相对不受自变量个数的影响，结果更为可靠。本例包括多个自变量，建议报告调整R²=0.487。表明“所有自变量” 解释“训练比赛满意感”的48.7%变异。
②若德宾沃森检验若结果在0-4之间，基本可认为数据独立性符合。本例的德宾沃森值为1.761，符合独立性。

第二个结果为方差分析（ANOVA）：

主要探讨模型的是否成功建成。
本案例F=24.464，P<0.001，说明至少有一个自变量解释了一部分的因变量的变异，从而使得回归变异变大，残差变异减少，模型成功建立。
值得注意的是，本题“平方”和即变异程度（离均差平方和），R²=回归变异平方和/总的平方和=1807.759/3562.760=0.507。因此方差分析和R²结果同出一源，方差分析侧重于分析模型是否成功，R²侧重于探讨模型有多成功(相当于效应量)。
如果P<0.05，就说明多重线性回归模型中至少有一个自变量的系数不为零。同时，回归模型有统计学意义也说明相较于空模型，纳入自变量有助于预测因变量，或说明该模型优于空模型。

第三个结果，回归分析的主要结果：

计算回归系数、并对回归系数进行假设检验，探讨影响因素。

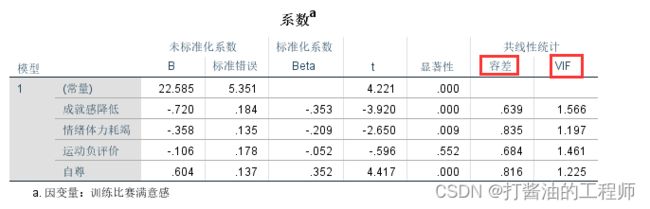
本研究结果显示：
①成就感降低（b=-0.72，β=-0.353，P<0.001）、情绪体力耗竭（b=-0.358，β=-0.209，P=0.009）和自尊（b=0.604，β=0.352，P<0.001）均会影响训练比赛满意感。其中，成就感降低和情绪体力耗竭负向预测（因为回归系数为负）训练比赛满意感，而自尊正向预测（因为回归系数为正）训练比赛满意感。
②运动负评价不会影响训练比赛满意感（b=-0.106，β=-0.052，P=0.552）。
③共线性统计包括方差膨胀因子（VIF）和容差两个指标，事实上，VIF=容差的倒数（1/容差），我们只需要判断其中一个指标即可。如果容忍度小于0.1（或方差膨胀因子大于10），提示数据存在多重共线性。在本研究中，所有容忍度值都大于0.1（最小值为0.639），说明本研究自变量多重共线不严重。

第四个结果，计算残差和预测值

可以通过下表来看预测值和残差结果：

在数据库中，可以发现增加了PRE_1（预测值）和RES_1（残差） ，两组相加，刚好是y“训练比赛满意感”。

第五个结果，残差直方图和P-P图。

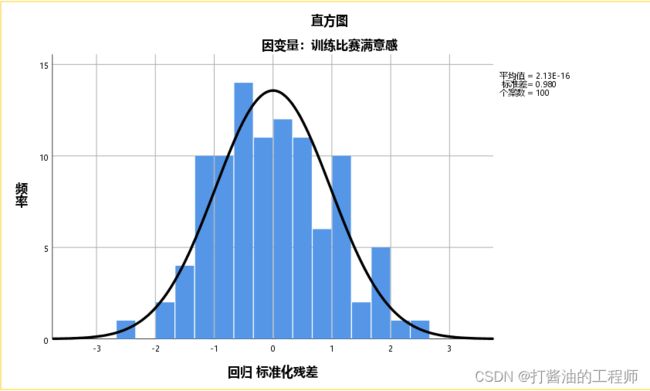
可以看出，本例残差直方图服从正态分布，且均数接近于0，标准差接近于1（标准正态分布），这意味着线性回归在正态性条件是达到的。P-P图也表明满足正态性条件。

第六个结果，残差图。

残差图的x、y轴分别是因变量预测值的标准化值和残差的标准化值（一般x轴是预测值的标准化值）。本例从图形来看，标准化残差图分布在0值周围，基本是上下对称分布，分布特征不随预测值的增加而发生改变，意味着数据方差齐性、独立性条件符合。

五、规范报告

规范报告有多种方式，本公众号只提供一种方式供参考。

1、规范表格

2、规范文字

采用多元线性回归分析结果显示，回归方程显著，F=24.464，p<0.001。其中，成就感降低（β=-0.353，P<0.001）、情绪体力耗竭（β=-0.209，p=0.009）显著负向预测训练比赛满意感，自尊（β=-0.352，p<0.001）显著正向预测训练比赛满意感。运动负评价不能预测训练比赛满意感（β=-0.596，p=0.552）。这些变量共解释训练比赛满意感48.70%的变异。

六、划重点

1、多元线性回归分析本质上是探讨变量之间相关关系，只有在理论上满足多个自变量与因变量之间存在因果关系，才可开展回归分析。此外，即使回归分析显著，在解释因果关系也需谨慎。
2、多元线性回归中的因变量需满足连续型变量；自变量可以分类变量、次序变量和连续型变量。
3、如果自变量为连续型变量，则需要满足自变量和因变量之间存在线性关系，如果不能满足，则不能采用线性回归分析，这可通过散点图来判断线性关系。
4、回归分析还需满足独立性、方差齐性和正态性，各自变量之间不存在多重共线性。
独立性采用德宾-沃森（D-W）残差相关性检验；方差齐性采用残差散点图来检验；正态性采用残差正态分布图和P-P图来判断。
5、如果回归分析只是建立自变量与因变量之间关系，无须根据自变量预测因变量的容许区间和可信度等，则方差齐性和正态性可以适当放宽。

Tips：如何用SPSS检验多重共线性

在SPSS中有专门的选项的。例如在回归分析中，线性回归-统计量-有共线性诊断。
多重共线性:自变量间存在近似的线性关系，即某个自变量能近似的用其他自变量的线性函数来描述。

多重共线性的后果∶

整个回归方程的统计检验P 偏回归系数的估计值大小明显与常识不符，甚至连符号都是相反的。比如拟合结果表明累计吸烟量越多，个体的寿命就越长。
在专业知识上可以肯定对应变量有影响的因素，在多元回归分析中却P>a，不能纳入方程
去掉一两个变量或记录，方程的回归系数值发生剧烈抖动，非常不稳定。

多重共线性的确认∶

做出自变量间的相关系数矩阵∶如果相关系数超过0.9的变量在分析时将会存在共线性问题。在0.8以上可能会有问题。但这种方法只能对共线性作初步的判断，并不全面。
容忍度( Tolerance ) :有Norusis提出，即以每个自变量作为应变量对其他自变量进行回归分析时得到的残差比例，大小用1 减决定系数来表示。该指标越小，则说明该自变量被其余变量预测的越精确共线性可能就越严重。陈希孺等根据经验得出∶如果某个自变量的容忍度小于0.1，则可能存在共线性问题。
方差膨胀因子( Variance inflation factor，VIF )∶由Marquardt于1960年提出，实际上就是容忍度的倒数。
特征根（Eigenvalue ) ︰该方法实际上就是对自变量进行主成分分析，如果相当多维度的特征根等于0，则可能有比较严重的共线性。
条件指数( Condition Idex ) :由Stewart等提出，当某些维度
的该指标数值大于30时，则能存在共线性。

多重共线性的对策︰

增大样本量，可部分的解决共线性问题
采用多种自变量筛选方法相结合的方式，建立一个最优的逐步回归方程。
从专业的角度加以判断，人为的去除在专业上比较次要的，或者缺失值比较多，测量误差比较大的共线性因子。
进行主成分分析，用提取的因子代替原变量进行回归分析。进行岭回归分析，它可以有效的解决多重共线性问题。
进行通径分析( Path Analysis )，它可以对应自变量间的关系加以精细的刻画。Spss可以进行比较基本的通径分析，但复杂的模型需要使用SPSS公司的另外一个软件AMOS来进行。