2021年数模国赛A题国二摘要及经验分享（回忆篇，附部分代码）

以2021年数模国赛A题为例，主要分享内容有：如何写好国赛摘要、部分解题思路和排版技巧。接下来，干货走起。

题目重述：“ FAST ”主动反射面的形状调节
中国天眼（ FAST ）由主动反 射面、信号接收系统（馈源舱）以及相关的控制、测量和支承系统组成。将反射面调节为工作抛物面是主动反射面技术的关键，有一个理想的工作抛物面可以获得天体电磁波经反射面反射后的最佳接收效果，该过程的完成主要依赖于下拉索和促动器配合完成。

上图是 FAST 在观测时的剖面示意图， C 点是基准球面的球心，馈源舱接收平面的中心只能在与基准球面同心的一个球面上移动，两同心球面的半径差为 F=0.466R （其中 R 为基准球面半径，称 F/R 为焦径比）。当 FAST观测某个方向的天体目标 S 时，馈源舱接收平面的中心被移动到直线 SC与焦面的交点 P 处，调节基准球面上的部分反射面板形成以直线 SC 为对称轴、以P 为焦点的近似旋转抛物面面（工作抛物面）。

本文根据问题建立数学模型，并设计求解方法解决如下问题：
问题一：当待观测天体S 位于基准球面正上方时，建立此时的理想抛物面方程
问题二：当待观测天体S 位于特定位置时，建立理想抛物面；调节促动器使反射面贴合理想抛物面；求出理想抛物面的顶点坐标，以及调节后反射面3 00 米口径内的主索节点编号、位置坐标、各促动器的伸缩量等结果。
问题三：基于问题二的调节方案，计算调节后馈源舱的接收比，并与基准反射球面的接收比作比较。
论文摘要：

部分解题思路及结论：

1）问题一：
以基准球面的球心为原点的xoz平面示意图如图2所示，基准面为半径R=300m的球面，照射范围内工作抛物面的口径为300m，工作抛物面的焦距F=0.466R，工作抛物面位于基准球面的内侧，二者的最大距离为0.6m，且工作抛物面的顶点与基准面重合，即抛物面顶点为M1(0,0，-300)。

由 xoz 平面示意图可得理想抛物面的xoz 平面表达式如式(1)所示：
$$z=a{x}^3-300（1）$$
式（1）绕z 轴旋转可得理想工作抛物面的表达式如式（2）所示：
$$z=a(x^2+y^2)-300（2）$$
空间球面的表达式如式（3）所示：
$$x^2+y^2+z^2=300（3）$$
当工作面的口径为r1=150m时，对应于相同z值（即高度）的基准球面的口径即为r2 =150.6m，则
$$z=sqrt(300^2-r_2^2)（3）$$

解得 z=-259.46。
将抛物线上的点（150，z）代入式（1），可得a =0.0018
综上可得该情况下理想抛物面的表达式为图片。
接下来使用Matlab对理想抛物面进行仿真，如下图所示。

由图3可看出，理想抛物面完全位于基准球面的内侧，其与基准球面的法向距离较小，基本符合促动器可伸缩的范围要求，同时也验证了假设的合理性。工作抛物面的口径随着z坐标的增加会一直增大，即抛物线到圆弧的法向距离会持续增加。但促动器的径向伸缩范围为0.6～+0.6米，故促动器实际伸缩范围高于 0 .6 m 的伸缩均按 0 .6 m 处理。

2）简述剩余图文
找出所有300m 口径对应的主索节点位置坐标，其可视化图如下图所示。

定义目标函数为所有边长相对变化率，找到目标函数最小值对应的Q即可。每个主索节点周围均有6条边,设其初始长度为L1-L6，经调节后长度为L1’-L6’，目标函数则为

目标函数的求解结果如下图所示。由图可知，当目标函数为最小值，即为2.364 时，最优Q值为0.47。

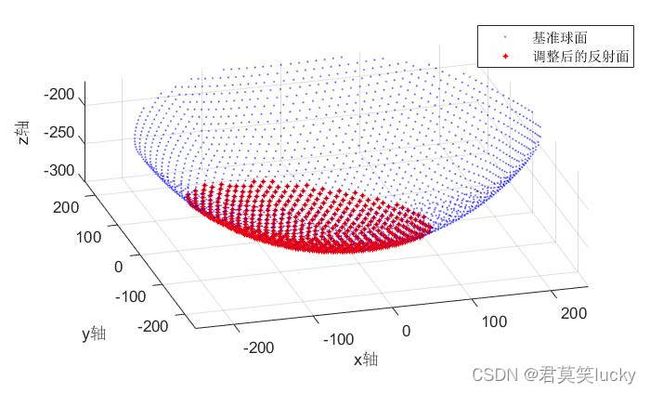
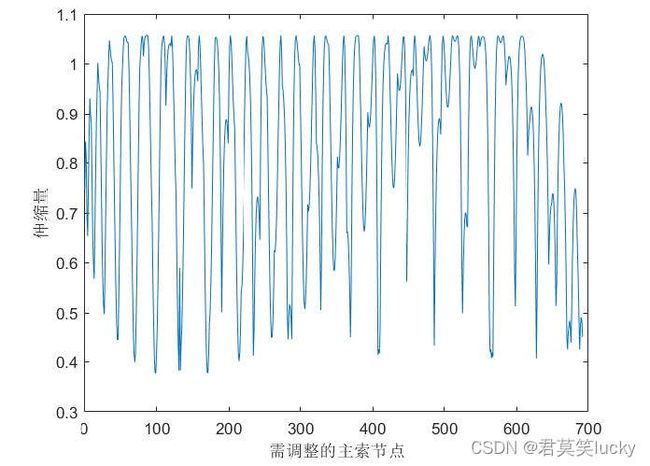
理想抛物面方程经过平移、旋转操作后，位于照明区域内的主索节点模拟图如下图所示。

优化前后需调整主索节点对应伸缩量的变化如下所示：

可看出优化后的主索节点对应伸缩量明显下降，并符合一定的规律，索命优化是有效的。

反射定律指光射到一个界面上时，其入射光线与反射光线成相同角度。问题三中对一块反射面板而言，其反射光线路径受到入射光线路径及其下下拉索具体方向的影响，简化示意图如下图所示。

在三维空间中，反射光线相当于入射光线绕法向量旋转180°。已知馈源舱的直径为1m，反射光线可能被馈源舱接收，也可能不被接收，具体示意图分别如图(a)、(b)所示。如图(a)所示，反射光线未能被直径为1m 的馈源舱接收；如图(b)所示，反射光线完全被直径为1m 的馈源舱接收。
图(a)

图(b)

总结：
这次国赛是我和康姐在大四考研期间抽出时间参加的，2个人一起努力3天，期间多亏康姐加油打气及指导老师的用心指导才坚持下来并有幸获得国奖。
在比赛期间，因为任务量比较大且比正常队伍少一个人，整体节奏比较慢。物理题目需要理解的地方很多，在对题目有一个全面的理解后，往往就需进行编程仿真，对编程要求较高。在比赛中，编程和应用能力决定了所获奖次的下限，而论文编写也是非常重要的，好的论文手往往能将论文提升一个档次。这次比赛中，编程花费了很长时间。因时间问题，没有做灵敏度分析且赛后回忆起来发现结果其实还可以再优化！！不过这篇论文对于当时的我俩已经尽力了，毕竟也是俺人生第一次尝试将近40个小时不休息。。。
摘要方面叙述一定要严谨，用简短的语言将方法、模型和结论陈述出来，同样也是这次比赛，我第一次在摘要中加入公式，在拜读优秀论文时，发现对公式也进行了展示。（摘要一定要逐字检查，决定能否获奖）
国赛的论文排版要求紧凑，没有的明显空白处，如果有空白的地方，在不改变论文叙述流畅的前提下，要对内容进行增添或删减。
队友之间的沟通配合也是非常重要的，要多沟通，保证将做题思路及时表述在论文中。
部分代码：

  %% 绘制FAST索网三维图  
  [~,~,node]=xlsread('附件1.csv');  
  [~,~,Connect]=xlsread('附件3.csv');  
  node=string(node);Connect=string(Connect);  
  node(1,:)=[];Connect(1,:)=[];  
  figure(1)  
  hold on  
  a=[];b=[];c=[];  
  for i=1:size(Connect,1)  
     a=find(node(:,1)==Connect(i,1));  
     b=find(node(:,1)==Connect(i,2));  
     c=find(node(:,1)==Connect(i,3));  
     plot3(double(node([a,b,c],2)),double(node([a,b,c],3)),double(node([a,b,c],4)),'b-')  
     scatter3(double(node([a,b,c],2)),double(node([a,b,c],3)),double(node([a,b,c],4)),'r')    
  end  
  xlabel('x轴');  
  ylabel('y轴');  
  zlabel('z轴');  
  grid on   
  %% 对理想抛物面进行可视化 
  figure(2)   
  plot3(a(:,1),a(:,2),a(:,3),'o');  
  hold on  
  plot3(b(:,1),b(:,2),b(:,3),'*')  
  plot3(b(:,4),b(:,5),b(:,6),'r')  
  plot3(b(:,4),b(:,5),b(:,6),'-')  
  t=-150:1:150;  
  [x,y]=meshgrid(t);  
  z=0.0018*(x.*x+y.*y)-300;  
  mesh(x,y,z)  
  colorbar  
  axis([-250 250 -250 250 -300 -260])  
  xlabel('x轴');  
  ylabel('y轴');  
  zlabel('z轴');  
  legend('主锁节点','上端点','下端点')  
  grid on 

在文章最后，感谢自己本科期间数模竞赛中遇到的所有指导老师和队友，相逢即有缘，感恩有你。如果没有朴老师，我可能其中也有我的同班同学我晨姐、康姐、尤姐，当然还要感谢我周哥（我承认有好几次比赛少人，常拉他帮忙，而最终都没能带他拿个不错的奖，深感抱歉图片，并祝他最终能上岸哈工程或者考公上岸）。