基于深度学习的超分辨技术介绍

基于深度学习的超分辨技术介绍

Deep Learning for Image Super-Resolution(SR) : A Survey
笔记作者：瀚
2023年夏于 国防科技大学

I. INTRODUCTION

超分辨技术简单来说是一种从低分辨率图像中生成高分辨的技术。传统方法也有一些基于预测或边缘的方法来进行达成超分辨的目的。本文主要介绍基于深度学习的超分辨。文章介绍从下面三个方面展开：

1. 超分辨问题的抽象化提出，benchmark数据集，性能评价指标，各种基于深度学习的SR算法。
2. 不同基于深度学习的SR算法各自的优势和局限。
3. 目前SR领域亟待解决的问题和发展趋势。

---

II. Problem Setting and Terminology

一般抽象超分辨问题如下：
$$I_x=\mathcal{D}(I_y;\delta )\text{\hspace{1em}(1)}$$
Where $\mathcal{D}$ denotes the degradation mapping function. $I_y$ denotes the HR image, $I_x$ denotes the LR image and $\delta$ is the parameters of the degration process.

由于我们一般不知道退化过程和过程中的参数的情况，所以对于超分辨就是一个求近似解的过程：
$$\widehat{I_y}=\mathcal{F}(I_x;\theta )\text{\hspace{1em}(2)}$$
其中 $\widehat{I_y}$ 是我们对于 HR 图像的一个近似解，$\theta$ 是 $\mathcal{F}$ 的参数。

所以我们一般希望解决的问题如下描述：
$$\mathcal{D}(I_y;\delta )=(I_y\otimes k){\downarrow }_s+n_{\varsigma },\{k,s,\varsigma \}\subset \delta \text{\hspace{1em}(3)}$$
式3表示退化过程可以通过对HR图像进行卷积下采样后加噪声来表示。其中${\downarrow }_S$表示尺度因子为$s$的下采样，$\otimes$表示卷积。一般设置$n_{\varsigma }$为加性白噪声 。如何求解从LR到HR的问题就变成了如何求解式3。那么如何求解式3呢？聪明的人类列出来下面的公式：
$$\hat{\theta }=\arg \underset{\theta }{\min }\mathcal{L}({\hat{I}}_y,I_y)+\lambda \Phi (\theta )\text{\hspace{1em}(4)}$$
没错，这是一个优化问题，

• $\hat{\theta }$：表示参数的估计值。
• $\arg {\min }_{\theta }$：表示求使得下面表达式最小化的参数值($\theta$)。
• $\mathcal{L}({\hat{I}}_y,I_y)$：表示损失函数，用来衡量估计值(${\hat{I}}_y$)和真实值($I_y$)之间的差异。
• $\lambda$：是一个正则化项的超参数，用于平衡损失函数和正则化项之间的重要性。
• $\Phi (\theta )$：表示正则化项，用来约束参数值，防止过拟合。

那么显而易见，对于$\mathcal{L}({\hat{I}}_y,I_y)$的设计是整个问题的核心。设计优秀的损失函数就可以送入网络解决优化方程，通过解决优化方程就可以找到退化方程中的参数，找到了参数就可以将 $\widehat{I_y}$ 求解出来了。

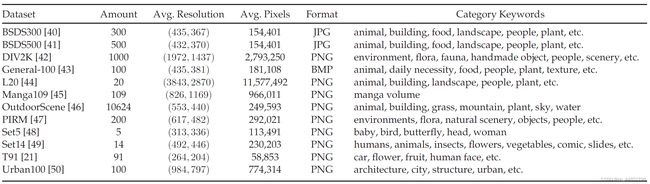
III. 数据集

IV. 评价指标

结构相似性SSIM和信噪比峰值PSNR、MOS、NIMA、FSIM、NIQE…不展开介绍，更多信息请Google例如 “Image Quality Assessment FSIM”。

SSIM参考：

Z. Wang, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli, “Image quality assessment: From error visibility to structural similarity,” IEEE Trans. Image Process., vol. 13, no. 4, pp. 600–612, Apr. 2004.

V. Supervised SR

a. Frameworks

由于超分辨需要包含上采样和卷积网络两个模块，其中上采样负责实际上提升分辨率，卷积网络负责位置信息的预测，所以基于监督的SR一般有下面几种形式：

1. Pre-upsampling：首先进行上采样，然后对上采样后的模糊图像进行CNN修正。这里面上采样算法的设计是关键，决定后面送进网络的图像的初始质量，一般使用传统算法。缺点是由于上采样后图像尺度比较大，所以后续CNN中的参数量比较大。
2. Post-upsampling：首先进行CNN网络修正，再进行上采样。这样可以避免参数量大的问题，但缺点显然易见，首先是由于最后一步上采样，所以之前的CNN网络应该提前知道尺度因子，也就意味着对于每一个不同的尺度因子都需要重新进行CNN训练。同时对于大尺度的情况，可能会导致结果不稳定。
3. Progrecessive upsampling：其实就是把 Post-upsampling 的一步到位拆成多步，每步升一点作为下一步的输入。比如希望将图片a放大8倍，那么这个方法就是进行3次放大两倍的Post-upsampling。
4. Iterative up-and-down Sampling：来回放大缩小，考虑到每次上采样生成的信息可能不是最准确的，所以上采样后会再进行下采样来抛弃一部分生成的信息。有点走两步退一步的感觉。

总结下来 Pre-upsampling 属于一步升天然后夯实基础，Post-upsampling 属于沉淀沉淀顶峰相见，Progrecessive upsampling 是不骄不躁稳步向前，Iterative up-and-down Sampling 是起起伏伏但是稳中向好。:-p

b. Loss Functions

我们提到了超分辨是一个优化问题，并给出了优化方程（式4）。当时对于其中的 $\mathcal{L}({\hat{I}}_y,I_y)$ 我们说它表示真实和实际的差异，那么这个差异怎么量化的表示，是这一节的讨论的重点。

1. Pixel loss

Pixel loss是进行逐像素的对比，由于PSNR作为评价指标，是进行两图片像素级的对比。所以Pixel loss非常适合当作损失函数。缺点是生成的图片缺少纹理细节，缺少高频分量。
$${\mathcal{L}}_{p}ixel(\hat{I},I)=\frac{1}{hwc}\sum _{i,j,k}\sqrt{({\hat{I}}_{i,j,k}-I_{i,j,k}{)}^2+{ϵ}^2}\text{\hspace{1em}(5)}$$

$h,w,c$ 分别表示长、宽和通道数。

2. Content loss

Content loss是基于语义差异的损失函数，引入分类网络。简单来说是通过抽取特征层送入分类网络进行欧氏距离的计算。所以两个被认定为同一类别的像素被认为欧氏距离为0。所以损失函数的效果与分类网络有直接关系。
$${\mathcal{L}}_{c}ontent(\hat{I},I;\varphi ,l)=\frac{1}{h_l{w}_l{c}_l}\sum _{i,j,k}\sqrt{({\varphi }_{i,j,k}^{(l)}(\hat{I})-{\varphi }_{i,j,k}^{(l)}(I){)}^2}\text{\hspace{1em}(6)}$$

${\varphi }^{(l)}$ 表示鉴别网络的第 $l$ 层。

3. Adversarial loss

对抗性损失引入GAN网络，由于在监督学习中我们对 $I_y$ 是已知的，所以GAN中的生成器和鉴别器非常明确，即生成器（${\hat{I}}_y$），鉴别器（$I_y$）。GAN网络可以使用交叉熵或其他改进的函数作为损失函数。

Open issues & future directions

网络设计：将网络关注更多维度上的信息、局部和全局的信息…

学习策略：损失函数的设计和BN层的重新设计（因为有一些论文提出目前的BN不是超分辨问题的最佳选择，如下）…

B. Lim, S. Son, H. Kim, S. Nah, and K. M. Lee, “Enhanced deep residual networks for single image super-resolution,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. Workshops, 2017, pp. 1132–1140.

Y. Wang, F. Perazzi, B. McWilliams, A. Sorkine-Hornung, O. Sorkine-Hornung, and C. Schroers, “A fully progressive approach to single-image super-resolution,” in Proc. IEEE/ CVF Conf. Comput. Vis. Pattern Recognit. Workshops, 2018, pp. 977–97709.

R. Chen, Y.Qu, K. Zeng, J.Guo, C. Li, and Y. Xie, “Persistentmemory residual network for single image super resolution,” in Proc. IEEE/ CVF Conf. Comput.Vis. Pattern Recognit.Workshops, 2018, pp. 922–9227.

评价指标：更全面更具代表性的指标。

超分辨类型：无监督或半监督的超分辨算法设计。

应用于真实世界：在真实世界中会存在加性噪声等退化，对于无法预测的噪声会对网络生成的内容造成挑战。