信号完整性分析基础知识之传输线和反射（五）：较短阻抗不连续的传输线、残桩和末端容性负载引起的反射

首先来一首定场诗：难难难，道德玄，不对知音不可谈。对了知音谈几句，不对知音枉费舌尖。

较短不连续点引起的反射

很多时候，板载走线的宽度必须要收窄，特别是经过PF区域或者拥挤区域。如果传输线的某一小段宽度变细，特性阻抗也会明显增加，那么阻抗会变化多少，并且变细的长度超过多少会出现问题呢？

三个特性决定了小段传输线宽度变化的影响：不连续点的时延，不连续点的阻抗，以及信号的上升时间。如果时延比上升时间更长，换句话说，不连续性在电学上很长——反射电压将饱和。反射率的最大值将和不连续点之前的反射有关。

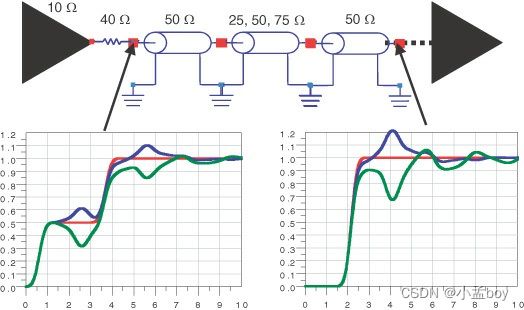
例如，如果线宽收窄导致阻抗从50Ohm变化到了75Ohm，反射率就是0.2。下图显示了来自长传输线不连续性的反射和传输信号的一些示例。

随着不连续阻抗的变化，传输线电路中的反射和传输信号具有较长但均匀的不连续性。

阻抗不连续导致信号来回震荡，引起反射噪声。这就是为什么一定要在内部互连中保持均匀特性阻抗。为了保证电压反射噪声小于5%，需要保证传输线的特性阻抗变化小于10%。
请注意，无论来自第一个不连续点的反射是什么，它都将与第二个不连续点的反射相等但符号相反，因为 Z 1和 Z2 将反转。如果不连续性可以保持较短，则两端的反射可能会抵消，并且对信号质量的影响可以忽略不计。下图显示了具有 25 欧姆的短长度不连续性的反射和传输信号。

具有较短但均匀不连续性的传输线电路中的反射和传输信号，不连续性的时间延迟从上升时间的 0% 增加到 40%。

如果不连续位置的时延小于上升时间的20%，那么不连续点将不会出现问题，和之前的结论一致。也即是说，最大可接受的阻抗不连续长度就是：

 其中Lenmax就是最大不连续长度，RT是上升时间。

 例如，如果上升时间为 0.5 纳秒，则短于 0.5 英寸的收缩可能不会造成问题。如果不连续的时间延迟可以保持在上升时间的 20% 以下，则不连续的影响可以忽略不计。这与经验法则相同，即不连续的长度（以英寸为单位）应小于信号的上升时间（以纳秒为单位）。

 短桩引起的反射

一段均匀的传输线经常会增加一些分支，来实现多个扇出，如果分支很短，就成为stub。BGA 封装上通常会发现一个短截线，以允许将所有引脚连接在一起，方便对焊盘进行镀金处理。总线在制造过程中被断开，留下小的、短的短截线连接到每条信号线上。
很难分析一个stub的影响，因为需要考虑所有的反射情况。当信号从驱动器发出，他会首先遇到分支点，这里会由于两条传输线线段的并联出线一个低阻抗，这会导致一个负反射返回源端。一小部分信号将继续沿着两个分支传播。当stub上的信号传输到stub末端，他会反射回分支点，然后又反射到stub的末端，这样在stub上来回震荡。同时，在与分支点的每次交互中，stub中的部分信号将返回源和远端。每个交界处都是一个反射点。
两个影响信号质量的重要因素是信号的上升时间和stub的长度。在这里我们假设stub位于传输线的中间，并和传输线具有相同的特性阻抗。下图展示了stub长度从20%上升时间到60%上升时间下的仿真反射信号和传输信号。

中间具有短桩的传输线上的反射和传输信号，短桩时延从上升时间的20%增加到60%

 作为粗略的经验法则，如果短截线长度保持短于上升时间空间范围的 20%，则短桩的影响可能并不重要。同样，如果stub比上升时间的 20% 长，它可能会对信号产生重要影响，必须进行仿真以评估它是否可以接受。
例如，如果驱动器的上升时间为 1 纳秒，则时间延迟短于 0.2 纳秒的短桩可能是可以接受的。短桩的长度约为 1 英寸。经验法则是：

这是一个简单易记的经验法则。例如，对于 1 纳秒的上升时间，让短桩短于 1 英寸。如果上升时间为 0.5 纳秒，则保持短桩短于 0.5 英寸。很明显，随着上升时间的减少，设计短桩以使其不影响信号完整性变得越来越难。
在BGA封装中，通常不可能避免在封装的制造中使用电镀短桩。这些短桩通常小于0.25英寸长。当信号的上升时间长于0.25nsec时，这些电镀短桩可能不会引起问题，但当上升时间下降到0.25nsec以下时，它们肯定会引起问题，并且可能需要为制造没有电镀短桩的封装支付额外费用。 

容性终端引起的反射

所有真实的接收器都有一些门输入电容，典型值为2pF。此外，接收器的封装信号引脚和返回路径之间也会有大约1pF的电容。如果传输线末端有三个存储器件，负载大约10pF。
如果信号在传输线上传输，并在末端遇到一个理想电容，实际的瞬时阻抗是由反射率决定，会随时间变化。毕竟，电容的阻抗在时域下：

Z是电容的瞬时阻抗，C是电容的容值，V是信号的瞬时电压。
如果信号的上升时间比电容充电时间短，在初始时间电容器的电压会上升非常快，阻抗很小。但是随着电容充电，穿过电容器的电压会越来越小，变化率dV/dt降低，这会造成电容器阻抗迅速增加，如果时间足够长，随着电容器充满电后，其阻抗相当于开路。
这意味着反射率是随时间变化的。反射信号会先下跌然后上升到近似开路状态。实际的表现取决于传输线的特性阻抗、电容器的电容以及信号的上升时间。下图展示了2pF,5pF,10pF电容仿真结果。

上升时间0.5ns，远端容性负载的传输线上反射和传输信号。

 传输电压模式的长期响应看起来像电阻器对电容器充电。电容器的存在过滤了上升时间，并充当接收器信号的“延迟加法器”。我们可以估计新的上升时间和信号通过中点（即延迟加法器）转换的时间延迟的增加，因为它非常类似于 RC 电路的充电，其中电压以指数时间常数增加:

 

这个时间常数是电压上升到 1/e 或最终电压的 37% 所需的时间。 10%−90% 上升时间与 RC 时间常数的关系为： 

 在传输线末端有一个容性负载，看起来电压正在以 RC 行为充电。C是负载的电容。R是传输线的特性阻抗Z0.传输信号10-90的上升时间如果以RC充电为主，大致是:

例如，如果传输线特性阻抗50Ohm，电容10pF，10%-90%充电时间为2.2*50Ohm*10pF=1.1ns。如果初始信号上升时间比1.1ns的充电时间更短，线路末端电容性负载的存在将占主导地位，将决定接收器位置信号的上升时间。如果信号的初始上升时间比 10−90 的充电上升时间长，那么末尾的电容会给上升时间增加一个延迟，它会大致等于 10−90 的上升时间。
始终注意 10−90 RC 上升时间，它基于线路的特性阻抗和输入接收器的典型容性负载。当 10−90 上升时间与初始信号上升时间相当时，远端的容性负载将影响时序。 

一个典型情况是电容为 2 pF，特性阻抗为 50 欧姆。 10−90 上升时间约为 2.2 × 50 × 2 = 0.2 纳秒。当上升时间为 1 纳秒时，这个额外的 0.2 纳秒延迟加法器几乎看不出来，可能并不重要。但是当上升时间为 0.1 纳秒时，0.2 纳秒的 RC 延迟可能是一个重要的延迟加法器。当驱动在远端分组的多个负载时，在所有时序分析中包括 RC 延迟加法器很重要。
在接收器的 IBIS 模型中，输入栅极电容项是 C_comp 项。这将在任何电路仿真中自动包含栅极电容的影响。如果接收器中有 ESD 保护二极管，则该值可能高达 5–8 pF。通常，它可以保持低至 2–3 pF。