CNN-卷积神经网络
一、基本的神经网络结构
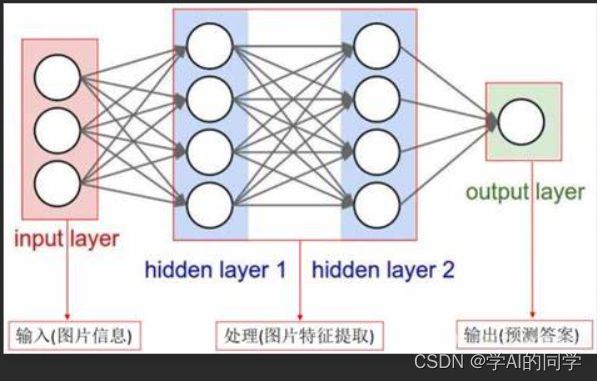
神经网络其实就是按照一定规则连接起来的多个神经元,输入向量的维度和输入层(Input Layer)神经元个数相同,分类问题的类别个数决定输入层(Output Lazyer)的神经元个数。第N层的神经元与第N-1层的所有神经元连接,称为全连接,输入层和输出层之间的层叫做隐藏层(HIdden Layer),因为它们对于外部来说是不可见的,层与层的每条连接上都有一个权值。
然而,用全连接神经网络处理大尺寸图像具有三个明显的缺点:
(1)首先,将图像展开为向量,会丢失临近像素的空间信息;
(2)其次,模型参数过多,因此效率低下,训练困难;
(3)同时,大量的参数也很快会导致网络过拟合。
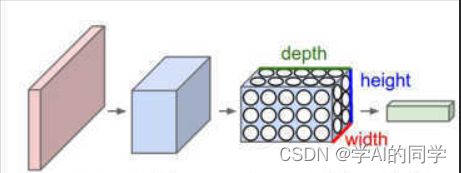
所以,提出了卷积神经网络,与普通的神经网络不同,卷积神经网络的各层中的神经元是三维排列的:宽度、高度、深度(这个深度指的是某层数据的第三个维度)。
CNN的每一层都将三维的输入数据变化为神经元的三维的激活数据并输出。
图像中,红色的输入层代表输入图像,所以它的宽度和高度就是图像的宽度和高度,它的深度是3(代表了RGB3种颜色通道)、接着是经过卷积运算(convolution)和池化运算(Pooling)之后的激活值(也可以看做一层神经元),再接着的下一部分的卷积池化层,最后的部分是一个深度为分类个数的输出向量。
二、卷积神经网络的构成
CNN由输入层、卷积层、激活函数、池化层、全连接层,通过将这些层叠加起来,就可以构建一个完整的卷积神经网络。
(1)输入层
卷积神经网络的输入层可以处理多维数据,
常见地,一维卷积神经网络的输入层接收一维或二维数组,其中一维数组通常为时间或频谱采样;
二维数组可能包含多个通道;二维卷积神经网络的输入层接收二维或三维数组;
三维卷积神经网络的输入层接收四维数组。
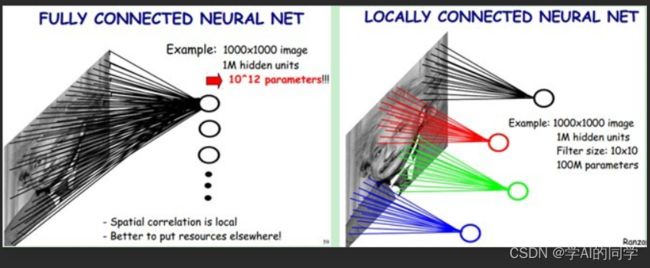
我们使用卷积处理图像,如果采用经典的神经网络模型,则需要读取整幅图像作为神经网络模型的输入(即全连接的方式),当图像的尺寸越大时,其连接的参数将变得很多,从而导致计算量非常大。因而,使用卷积对每个神经元局部进行感知,然后在更高层将局部的信息综合起来就得到了全局的信息。这种模式就是卷积神经网络中降低参数的目的,也可称为局部感受野。
(2)卷积层
卷积层的功能是对输入数据进行特征提取,其内部包含多个卷积核,组成卷积核的每个元素都对应一个权重系数和一个偏差量(bias vector),类似于一个前馈神经网络的神经元(neuron)。
卷积层内每个神经元都与前一层中位置接近的区域的多个神经元相连,区域的大小取决于卷积核的大小。
卷积核在工作时,会有规律地扫过输入特征,在感受野内对输入特征做矩阵元素乘法求和并叠加偏差量。
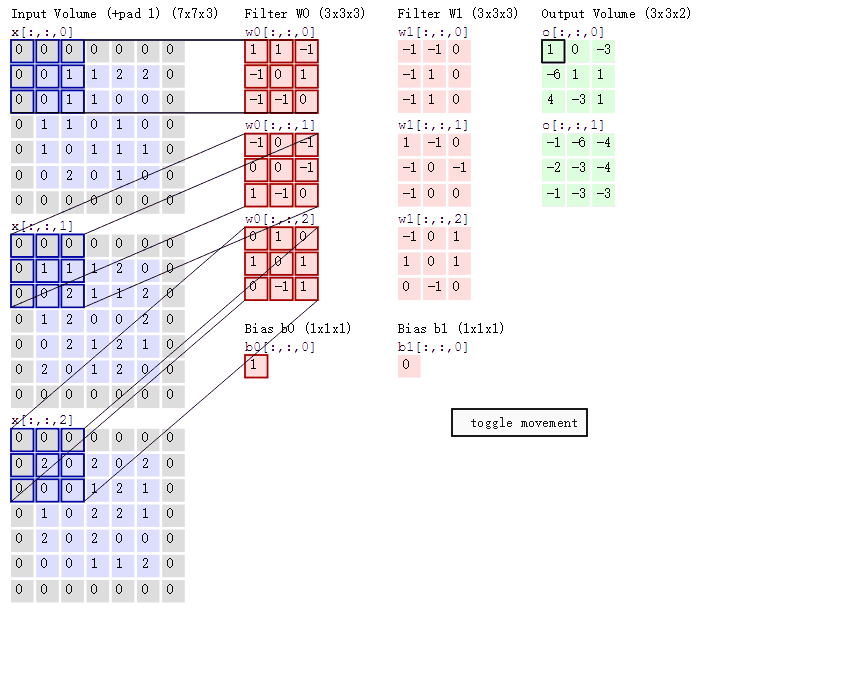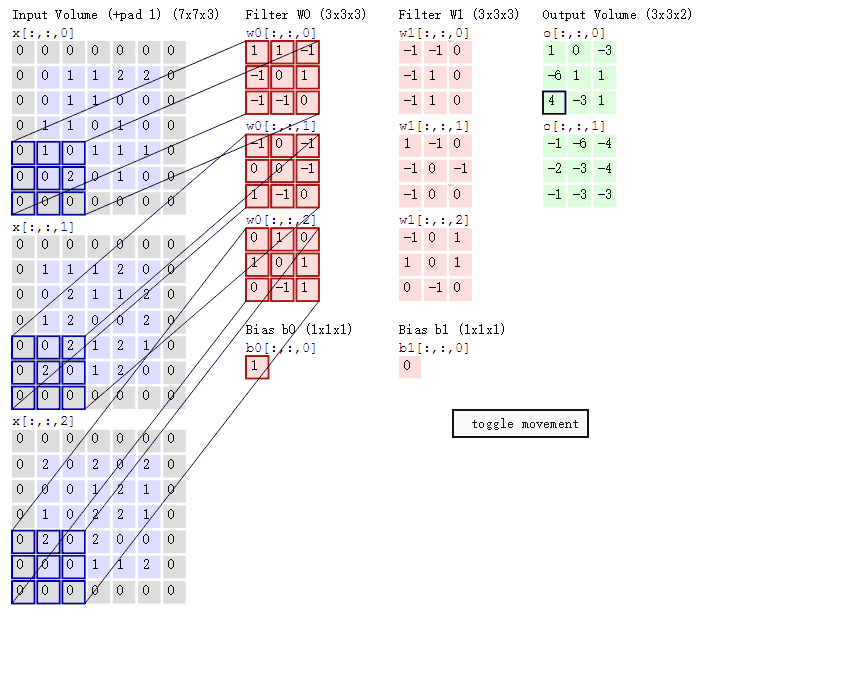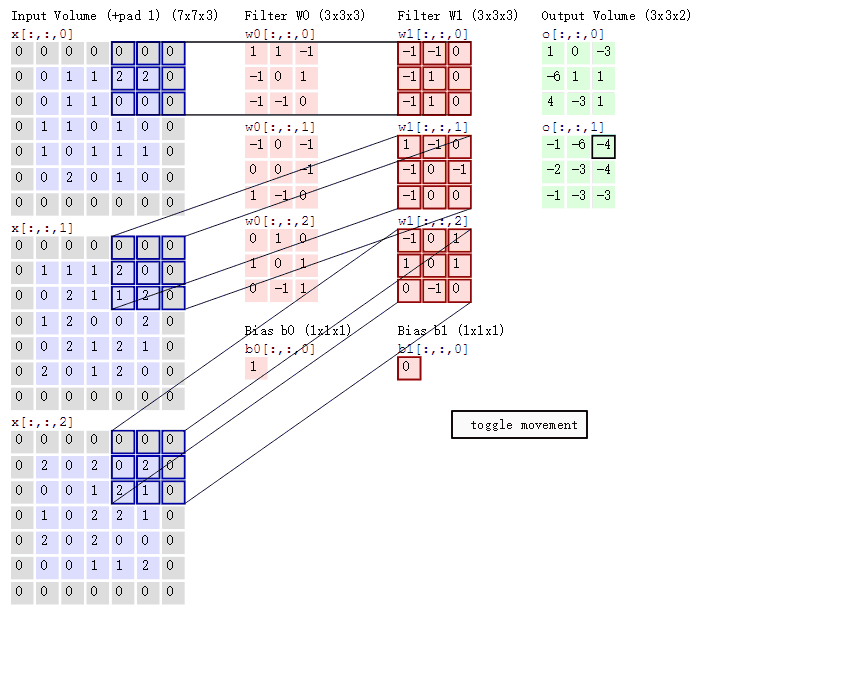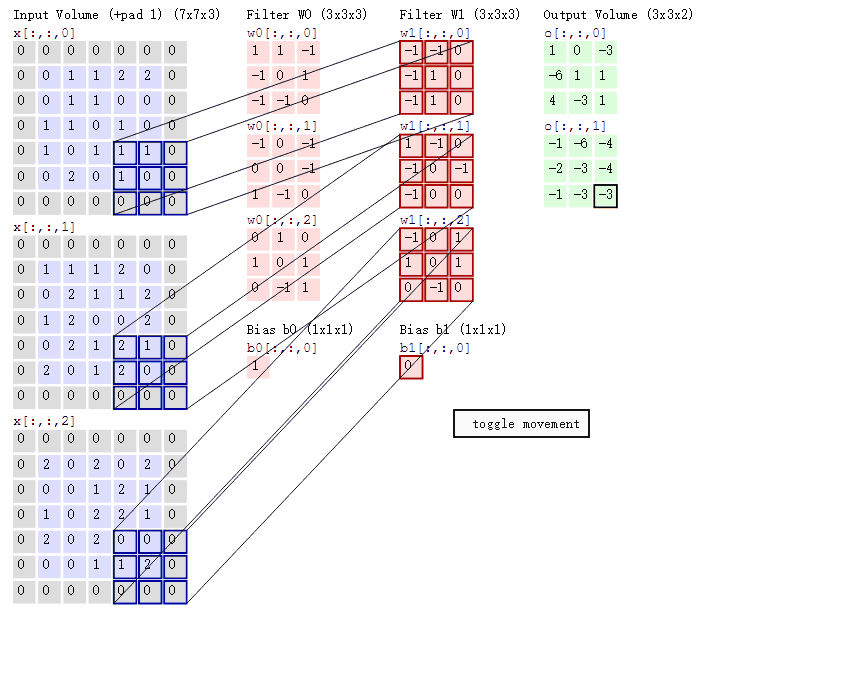
多通道卷积计算过程:
卷积层参数:
卷积层参数包括卷积核大小、步长和填充,三者共同决定了卷积层输出特征图的尺寸,是卷积神经网络的超参数。
其中卷积核大小(kernel_size:卷积核大小 [kernel_size * kernel_size] 大小的矩阵)可以指定为小于输入图像尺寸的任意值,卷积核越大,可提取的输入特征越复杂 。
卷积步长(stride:步幅大小,默认为1)定义了卷积核相邻两次扫过特征图时位置的距离,卷积步长为1时,卷积核会逐个扫过特征图的元素,步长为n时会在下一次扫描跳过n-1个像素。卷积时的采样间隔 设置步幅的目的是希望减小输入参数的数目,减少计算量。stride参数的值就是缩小的倍数,压缩一部分信息,或者使输出的尺寸小于输入的尺寸。
填充(padding):边缘填充的个数,填充添加到输入的所有四个侧面。默认值:0
padding:在输入特征图的每一边添加一定数目的行列,使得输出和输入的特征图的尺寸相同。
设置padding:如果没有padding,每次进行卷积后,原始图像的尺寸就会越来越小,所以没有办法设计层数足够多的深度神经网络。
希望每个输入特征图的每一块都能作为卷积窗口的中心,防止丢失图像边缘信息。
卷积层输出特征图的尺寸计算:
卷积层可用于减少空间维度,通过改变卷积核的步幅来调整输入。
W: input size
F: filter size
P: padding size
S: stride size
![]()
![]()
输出图像大小 = (输入图片大小 - 卷积和大小 + 2*填充值/步长
如果输出值包含分数,则取整数部分。
在当前层,每个通道都对应一个卷积核,且这个卷积核是独一无二的。
卷积过程中,输入层有多少个通道,filter就有多少个通道。
即:某一层filter的通道数 = 上一层特征图的通道数。
一般的图像都是三通道的,所以卷积核也应该为三个通道。filter的数量任意的,filter的数量决定了卷积后特征图的数量。
卷积核一般都把size设为奇数,主要是
1.保证锚点(卷积核的中心)刚好在中间,方便以模块中心为标准进行滑动卷积。
2.保证了padding时,图像的两边依然相对称。
(3)激活函数ReLU
使用激活函数,将数据进行非线性转换。
1.使用sigmoid时,涉及到指数运算,反向传播时求导涉及到除法,计算量大。而采用ReLu函数时,整个过程计算节省很多
2.sigmoid容易产生梯度消失(在sigmoid接近饱和区时,变换太缓慢,导数趋于0,这种情况会造成信息丢失。)
3.ReLu会使一部分神经元输出为0,造成网络的稀疏性,减少了参数之间的依存性,减少了过拟合的情况。
(4)池化层(pooling)
在卷积层进行特征提取后,输出的特征图会被传递至池化层进行特征选择和信息过滤。池化层包含预设定的池化函数,其功能是将特征图中单个点的结果替换为其相邻区域的特征图统计量。池化层选取池化区域与卷积核扫描特征图步骤相同,由池化大小、步长和填充控制。
池化层(Pooling Layer)是CNN中常见的一种操作,池化层通常也叫做子采样(subsampling)或降采样(Downsampling),在构建CNN网络时,往往是用在卷积层之后,通过池化层来降低卷积层输出的特征维度,在有效减少网络参数的同时还可以防止过拟合现象。
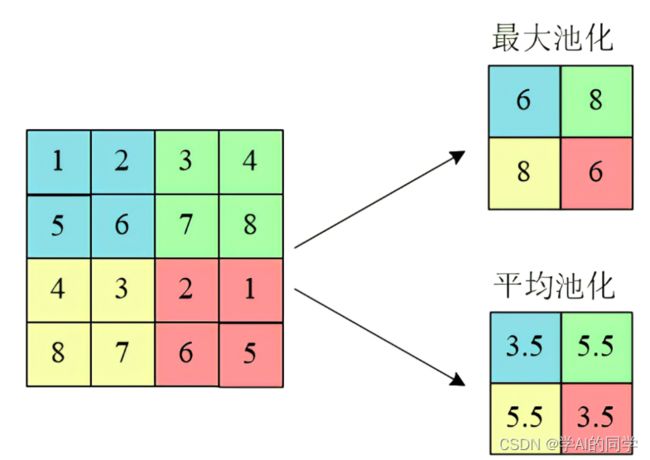
池化操作,我们经常用的池化操作,即最大池化(Max Pooling)和平均池化(Average Pooling),
最大池化是选择图像区域中最大值作为该区域池化后的值,方向传播的时候,梯度通过前向传播过程的最大值方向传播,其它位置梯度为0。
均值池化就是将选择的图像区中的所有值的平均值作为该区域池化后的值。
(5)全连接层
卷积神经网络中的全连接层等价于传统前馈神经网络中的隐含层。全连接层位于卷积神经网络隐含层的最后部分,并只向其它全连接层传递信号。特征图在全连接层中会失去空间拓扑结构,被展开为向量并通过激励函数
卷积神经网络中的卷积层和池化层能够对输入数据进行特征提取,全连接层的作用则是对提取的特征进行非线性组合以得到输出,即全连接层本身不被期望具有特征提取能力,而是试图利用现有的高阶特征完成学习目标。