蓝桥杯 第一场算法双周赛题解（前五题）

题目链接在此：第 1 场算法双周赛 - 蓝桥云课
为什么只有前5道题的题解呢？（懂的都懂~）

第一题 三带一

考察：简单逻辑判断

问题描述

小蓝和小桥玩斗地主，小蓝只剩四张牌了，他想知道是否是“三带一”牌型。
所胃三带一”牌型，即四张手牌中，有三张牌一样，另外一张不与其他牌相同，换种说法，四张手牌经过重新排列后，可以组成 AAAB型

输入格式

第一行输入一个整数T，代表斗地主的轮数。
接下来T行，每行输入一个长度为 4的字符串，代表小蓝的手牌。
字符{'A’,’2’,‘3’,’4’,’5’,’6’,’7’,’8’,’9,’X’,’J’,’Q’,’K’}对应代表牌面{A,2,3,4,5,6,7,8,9,10,J,Q,K}。
牌面中不包含大小王。

输出格式

输出行，每行一个字符串，如果当前牌是“三带一”牌型，输出 Yes，否则输出 No。

样例输入

AAAA
33X3
JQKX
6566
KKKQ

样例输出

No
Yes
No
Yes

说明

“四炸”牌型不属于“三带一”牌型。

评测数据范围

数据范围：$1\le T\le 50$。

字符中只包含:{A,2,3,4,5,6,7,8,9,X,J,Q,K}。

解题思路

第一题很简单，就是一个基本的逻辑判断，小细节就是对字符串排序可以减少判断量

代码

#include 
using namespace std;

int t;
string s;
signed main() {
    cin >> t;
    while (t--) {
        cin >> s;
        sort(s.begin(), s.end()); // 使其有序
        if (s[0] != s[3] && s[1] == s[2] && (s[0] == s[1] || s[2] == s[3])) cout << "Yes" << endl; // 说明是三带一
        else cout << "No" << endl;
    }    
    return 0;
}

第二题 数树数

考察：二叉树

问题描述

小蓝最近学了二又树，他想到了一个问题。
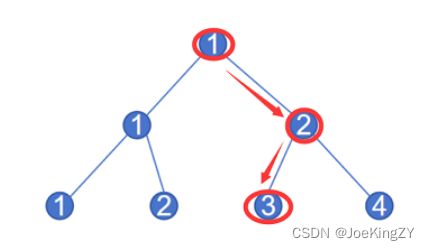
给定一个层数为n的满二叉树，每个点编号规则如下：

具体来说，二叉树从上向下数第p 层，从左往右编号分别为：$1,2,3,\mathrm{4...}{2}^{p-1}$。
小蓝给你一条从根节点开始的路径，他想知道到达的节点编号是多少。
例如: 路径是right - left，那么到达的节点是1-2-3，最后到了三号点，如下图所示。

输入格式

第一行输入两个整数n,q，n 表示完全二树的层数， q代表询问的路径数量。
接下来q 行，每行一个字符串 S，S 只包含字符{‘L’, ’R’}，’L’ 代表向左，’R’ 代表向右。

输出格式

输出q行，每行输出一个整数，代表最后到的节点编号。

样例输入

3 6
R
L
LL
LR
RL
RR

样例输出

2
1
1
2
3
4

说明

$2\le n\le 20,1\le q\le 10^3,1\le |S|\le n$
完全二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。
也就是说如果一个二叉树的层数为 $k$，且节点总数是$2^k-1$，则它就是满二又树。

解题思路

考察的是二叉树的性质
顺序遍历路径S，用一个变量记录到达的节点的id。节点id的编排规则：

再用id的值来计算目前所在的行数和列数。
如何用id来计算目前处于第几行的第几个节点呢？（这里用x代表id）
$$\begin{gathered} 行数=\lfloor lo{g}_{2}x\rfloor +1(\lfloor x\rfloor 表示对x向下取整) \\ 列数=x-2^{行数}+1 \end{gathered}$$
~请读者自行证明

代码

#include 
using namespace std;

int n, q;
string s;
signed main() {
    cin >> n >> q;
    while (q--) {
        cin >> s;
        int id = 1;
        for (char& i : s) { // 遍历字符串
            if (i == 'L') res *= 2; // 向左子节点走 -> id乘以2
            else res = res * 2 + 1; // 向右子节点走 -> id乘以2再加一
        }
        cout << res - (1 << (int)log2(res)) + 1 << endl; // 利用公式输出结果
    }
    return 0;
}

第三题 分组

考察：二分答案

问题描述

蓝桥小学要进行弹弹球游戏，二年级一班总共有 n 个同学，要求分成 k 个队伍，由于弹弹球游戏要求队员
的身高差不能太大，小蓝是班长，他对这个事情正在发愁，他想问你，如何最小化每个组之间的身高极差。
具体的，假设分成了 k 个组，第 i 组最高的人身高是 $H_{x_i}$，最矮的是 $H_{n_i}$，你被要求最小化表达式：
$max(H_{t_i}-H_{n_i}),1\le i\le k$。直白来说，你需要将 n 个元素分出 k 组，使得最大的极差尽可能小。你需要输出这
个最小化化后的值。

输入格式

第一行输入两个整数n, k。
第二行输入n 个整数: $h_1,h_2,h_3...h_n$，分别代表 n 个人的身高

输出格式

输出一个整数，代表最小值。

样例输入

5 3
8 4 3 6 9

样例输出

1

说明

样例分组情况：{3, 4}, {6}, {8, 9}。

评测数据规模

数据范围: $1\le k\le n\le 10^5,1\le h_i\le 10^9$

解题思路

二分答案其实就是二分+贪心
（不知道为什么出题人总是爱考二分答案~，这种题都有一个特征：要么就是最小值最大化，要么就是最大值最小化，符合某种单调性）
首先，每一个分组都是身高尽可能接近的同学，可以证明：每一个分组都是排好序后的连续的几位~（因为如果不是这样，每一组的最大身高差只会增，不会减，最多保持不变）
然后就好说了，先排序，排完序后二分最大身高值，双指针遍历数组（对其分组），如果超过了最大值，就分组加一，如果分组超过了k，说明不行。

代码

#include 
using namespace std;

const int N = 1e5 + 5;
int n, k, h[N];
bool check(int x) { // 经典check函数（懂的都懂)
    int c = 1; // 分组数
    for (int l = 0, r = 1; r < n; r++) { // 双指针
        if (h[r] - h[l] > x) { // 分组结果是[l, r)
            c++;
            l = r;
            if (c > k) return false; // 需要的分组数大于k了，不满足条件
        }
    }
    return true; // 满足
}
signed main() {
    cin >> n >> k;
    for (int i = 0; i < n; i++) cin >> h[i];
    sort(h, h + n); // 排序
    int l = 0, r = 1e9; // 二分
    while (l < r) {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1; // 注意是mid + 1，不然会死循环
    }
    cout << l; // 结果
    return 0;
}

第四题 健身

考察：完全背包DP

问题描述

小蓝要去健身，他可以在接下来的 1 ~ n 天中选择一些日子去健身
他有 m 个健身计划，对于第 i 个健身计划，需要连续的 $2^k$ 天，如果成功完成，可以获得健身增益$s_i$，如果中断，得不到任何增益。
同一个健身计划可以多次完成，也能多次获得健身增益，但是同一天不能同时进行两个或两个以上的健身计划。
但是他的日程表中有 q 天有其他安排，不能去健身，问如何安排健身计划，可以使得 n 天的健身增益和最大。

输入格式

第一行输入三个整数n,m,q
第二行输入q个整数，$t_1,t_2,t_3...t_q$，代表有其他安排的日期
接下来 m 行，每行输入两个整数 $k_i,s_i$。代表该训练计划需要 $2^{k_i}$天，完成后可以获得 $s_i$的健身增益

输出格式

一个整数，代表最大的健身增益和。

样例输入

10 3 3
1 4 9
0 3
1 7
2 20

样例输出

30

说明

在样例中2 - 3天进行计划2，5 - 8天进行计划3，10~10天进行计划1。

评测数据范围

$1\le q\le n\le 2\times 10^5，1\le m\le 50，1\le s_i\le 10^9，0\le g\le 20，1\le t_1<t_2<...<t_g\le n$

解题思路

首先，根据题意，我们不难发现必须在有安排的日子的空隙时间来健身，而在这段空隙时间，我们选择健身项目来健身，对于每一个项目，有时间$2^{k_i}$和收益$s_i$
聪明的小伙伴可能已经发现，这就是一个背包dp问题
由于健身计划可以重复多次，所以是完全背包问题，然后用滚动数组来优化空间。
由于要多次dp计算，可以用一个额外数组记忆化来保存

代码

#include 
using namespace std;
using ll = long long;

const int N = 2e5 + 5, M = 55;
ll n, m, q, t[N], k[M], s[M];
ll dp[N], mem[N]; // 记忆化数组
ll calc(int x) { // dp
    memset(dp, 0, n << 2);
    for (int i = 0; i < m; i++)
        for (int j = k[i]; j <= x; j++) { // 从小到大就是完全背包，从大到小是01背包~
            if (dp[j - k[i]] + s[i] > dp[j])
                dp[j] = dp[j - k[i]] + s[i];
        }
    return dp[x];
}
signed main() {
    cin >> n >> m >> q;
    for (int i = 1; i <= q; i++) cin >> t[i];
    for (int i = 0; i < m; i++) {
        cin >> k[i] >> s[i];
        k[i] = 1 << k[i]; // 需要花费的时间
    }
    t[q + 1] = n + 1; // 不遗漏最后的空隙时间
    ll res = 0;
    for (int i = 1; i <= q + 1; i++)
        if (t[i] - t[i - 1] - 1 >= 1) { // 有空隙时间
            if (!mem[t[i] - t[i - 1] - 1])
            	mem[t[i] - t[i - 1] - 1] = calc(t[i] - t[i - 1] - 1); // 记忆化
            res += mem[t[i] - t[i - 1] - 1];
        }
    cout << res;
    return 0;
}

Very important！！！

一定要开long long！一定要开long long！一定要开long long！

第五题 契合匹配

考察：KMP

问题描述

小蓝有很多齿轮，每个齿轮的凸起和凹陷分别用一个字符表示，一个字符串表示一个齿轮

如果两个齿轮的对应位分别是同一个字母的大小写，我们称这两个齿轮是契合的
例: AbCDeFgh 和 aBcdEfGH 就是契合的，但是 abc 和 aBC 不是契合的
这天，小蓝的弟弟小桥从抽屉里拿来了两个齿轮，小蓝想知道，这俩个齿轮是不是契合的。
特别需要注意的是，齿轮是环形的，所以是可以旋转的(顺时针和逆时针均可)，如果是契合的，小蓝还想
让你告诉他，最少将第一个齿轮旋转多少位，两个齿轮可以完全契合在一起
例如: AbbCd 与BcDaB，在将第一个齿轮逆时针旋转两位后，变成 bCdAb ，两个齿轮就完全契合在一起了

输入格式

第一行输入一个正整数n，代表两个齿轮的长度
第二行输入一个长度为的字符串S，代表第一个齿轮
第三行输入一个长度为n的字符串T，代表第二个齿轮

输出格式

第一行输出一个字符串: Yes 或者 No 。代表两个齿轮是否契合
如果可以契合，第二行输出一个整数，代表需要旋转的位数。
如果不可以契合，不用多余输出。

样例输入

5
AbbCd
BcDaB

样例输出

Yes
2

评测数据范围

数据范围: $1\le n\le 10^6$
保证字符串只包含大小写字母

解题思路

这题就是判断T是不是S的循环同构串，没什么其它好说的，就是很明显的KMP，直接把模板拿过来用就行了~
要注意顺时针和逆时针旋转都可以，所以从两种转法中取最小值

代码

#include 
using namespace std;

int n;
string s, t;
int Next[1000010]; // Next[i]：以第i个字符结尾的前缀字符串的最大前后缀字符串长
void getFail(string& p) {
    int plen = p.length();
    Next[1] = Next[0] = 0;
    for (int i = 1; i < plen; i++) {
        int j = Next[i];
        while (j && p[i] != p[j]) j = Next[j];
        Next[i + 1] = p[i] == p[j] ? j + 1 : 0;
    }
}
int kmp(string& s, string& p) {
    int slen = s.length(), plen = p.length();
    int j = 0;
    for (int i = 0; i < slen; i++) {
        while (j && abs(s[i] - p[j]) != 32) j = Next[j]; // 注意匹配的条件
        if (abs(s[i] - p[j]) == 32) j++; // 这里也是
        if (j == plen) return i - j + 1;
    }
    return -1;
}
signed main() {
    cin >> n >> s >> t;
    s += s; // 在尾部再加上一个s后，s的循环同构串就会出现在新的s中
    getFail(t);
    int res = kmp(s, t);
    if (res != -1) cout << "Yes" << endl << min(res, n - res); // 注意顺时针和逆时针旋转都可以
    else cout << "No";
    return 0;
}

比赛总结

前两道题还算比较顺利，但是到了后面疯狂出错，害，都习惯了
第三题是check函数写错了，两次都没检测出来
第四题刚开始超时了几次，因为忘了完全背包怎么写了，用多重背包的思路做的，后面因为没开long long，又错了好几次，有一个地方没开long long都不行，唉~，C++永远的坑（老是检查不出来）
第五题是因为没注意正着转和反着转都行。。。错了两次
排名就这样了，我太菜了
有什么问题欢迎在评论区留言~