leetcode每日一题-周复盘
前言
该系列文章用于我对一周中leetcode每日一题or其他不会的题的复盘总结。
一方面用于自己加深印象,另一方面也希望能对读者的算法能力有所帮助。
该复盘对我来说比较容易的题我会复盘的比较粗糙,反之较为细致
解答语言:Golang
周一:275. H 指数 II(middle)
题目描述:
给你一个整数数组 citations ,其中 citations[i] 表示研究者的第 i 篇论文被引用的次数,citations 已经按照 升序排列 。计算并返回该研究者的 h ******指数。
h 指数的定义:h 代表“高引用次数”(high citations),一名科研人员的 h 指数是指他(她)的 (n 篇论文中)至少 有 h 篇论文分别被引用了至少 h 次。
请你设计并实现对数时间复杂度的算法解决此问题。
示例 1:
输入: citations = [0,1,3,5,6]
输出: 3
解释: 给定数组表示研究者总共有 5 篇论文,每篇论文相应的被引用了 0, 1, 3, 5, 6 次。
由于研究者有3篇论文每篇 至少 被引用了 3 次,其余两篇论文每篇被引用 不多于 3 次,所以她的 h 指数是 3 。
复盘
该题跟上周日的题目是一样的,不过此题citaitons数组是有序的,要求对数的时间复杂度。
因此此题我们可以对论文篇数进行二分查找,mid<=citations[len_-mid] ;mid:有mid篇文章至少被引用了mid次,,citations[len_-mid]表示mid篇文章被引用了citations[len_-mid]次,
对此我们就可以进行二分的筛查,若mid<=citations[len_-mid]则表示答案是[mid,right]之间的
代码:
func hIndex(citations []int) int {
// 已排序直接二分
r:=len(citations)
l:=1
len_:=r
var mid int
for l<=r{
mid=l+(r-l)>>1
if mid<=citations[len_-mid]{
l=mid+1
}else{
r=mid-1
}
}
return r
}
周二:2003. 每棵子树内缺失的最小基因值(hard)
题目描述:
有一棵根节点为 0 的 家族树 ,总共包含 n 个节点,节点编号为 0 到 n - 1 。给你一个下标从 0 开始的整数数组 parents ,其中 parents[i] 是节点 i 的父节点。由于节点 0 是 根 ,所以 parents[0] == -1 。
总共有 105 个基因值,每个基因值都用 闭区间 [1, 105] 中的一个整数表示。给你一个下标从 0 开始的整数数组 nums ,其中 nums[i] 是节点 i 的基因值,且基因值 互不相同 。
请你返回一个数组 **ans ,长度为 n ,其中 ans[i] 是以节点 i 为根的子树内 缺失 的 最小 基因值。
节点 x 为根的 子树 包含节点 x 和它所有的 后代 节点。
示例 1:
输入: parents = [-1,0,0,2], nums = [1,2,3,4]
输出: [5,1,1,1]
解释: 每个子树答案计算结果如下:
- 0:子树包含节点 [0,1,2,3] ,基因值分别为 [1,2,3,4] 。5 是缺失的最小基因值。
- 1:子树只包含节点 1 ,基因值为 2 。1 是缺失的最小基因值。
- 2:子树包含节点 [2,3] ,基因值分别为 [3,4] 。1 是缺失的最小基因值。
- 3:子树只包含节点 3 ,基因值为 4 。1是缺失的最小基因值。
复盘
此题我并没有做出来,菜~,不过看完解析还是自己写出来了·····
此题关键点在于基因值是不重复的,因此找到基因为1的节点,如不存在那结果都为1,
若存在则至下而上去寻找最小缺失值,因为若不重复,其实不难发现除了价值为1节点往上的一条链路中,其他链路都缺失1,因此缺失值最小值都为1
因此我们只需至下而上去找每个节点它们的子树中存在的基因值有哪些,再得出最小缺失值即可
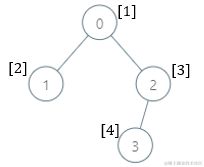
例如这一颗树
我们只需要管基因值为1的节点及它的父节点那一条链路,因为其他节点的缺失基因值都为1
从基因值为1的节点往上依次更新节点的缺失基因值,因为父节点显然包含子节点的所有基因值。
代码
func smallestMissingValueSubtree(parents []int, nums []int) []int {
n := len(parents)
ans := make([]int, n)
for i := range ans {
ans[i] = 1
}
node := slices.Index(nums, 1)
if node < 0 { // 不存在基因值为 1 的点
return ans
}
// 建树
g := make([][]int, n)
for i := 1; i < n; i++ {
p := parents[i]
g[p] = append(g[p], i)
}
vis := make(map[int]bool, n)
var dfs func(int)
dfs = func(x int) {
vis[nums[x]] = true // 标记基因值
for _, son := range g[x] {
if !vis[nums[son]] { // 避免重复访问节点
dfs(son)
}
}
}
// 直接从基因为1的节点开始dfs,由于父节点基因的集合是包含子节点的,因此mex递增即可
for mex := 2; node >= 0; node = parents[node] {
dfs(node)
for vis[mex] { // node 子树包含这个基因值
mex++
}
ans[node] = mex // 缺失的最小基因值
}
return ans
}
周三:2127. 参加会议的最多员工数(hard)
题目描述:
一个公司准备组织一场会议,邀请名单上有 n 位员工。公司准备了一张 圆形 的桌子,可以坐下 任意数目 的员工。
员工编号为 0 到 n - 1 。每位员工都有一位 喜欢 的员工,每位员工 当且仅当 他被安排在喜欢员工的旁边,他才会参加会议。每位员工喜欢的员工 不会 是他自己。
给你一个下标从 0 开始的整数数组 favorite ,其中 favorite[i] 表示第 i 位员工喜欢的员工。请你返回参加会议的 最多员工数目 。
示例 1:
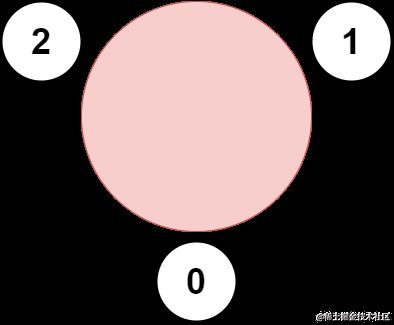
输入: favorite = [2,2,1,2]
输出: 3
解释:
上图展示了公司邀请员工 0,1 和 2 参加会议以及他们在圆桌上的座位。
没办法邀请所有员工参与会议,因为员工 2 没办法同时坐在 0,1 和 3 员工的旁边。
注意,公司也可以邀请员工 1,2 和 3 参加会议。
所以最多参加会议的员工数目为 3 。
复盘:
这个题我又又没做出来,hard还是太顶了,而且我对拓扑类的题也不是很熟悉。。。。。
这个题翻译过来就是其实就是一个图论的问题。
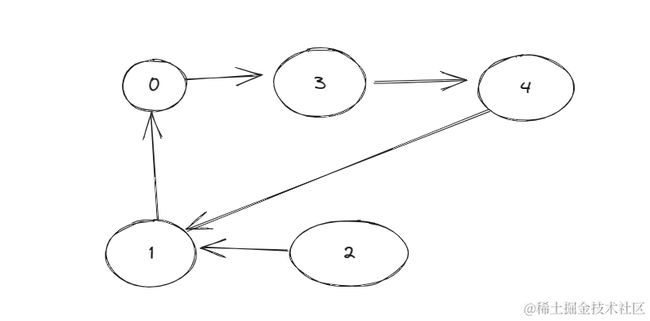
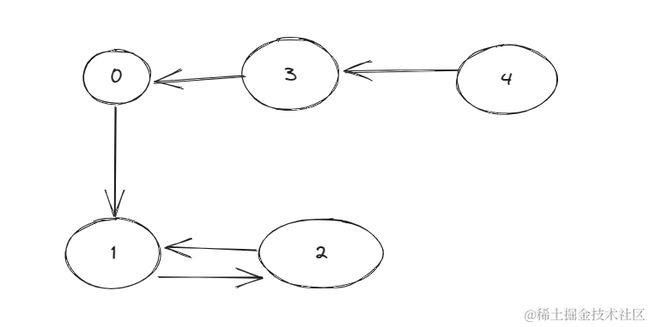
favorite = [3,0,1,4,1],例如这一种情况转换成图就是:
那是不是说这个题我们找出最大长度的一个环就可以了,
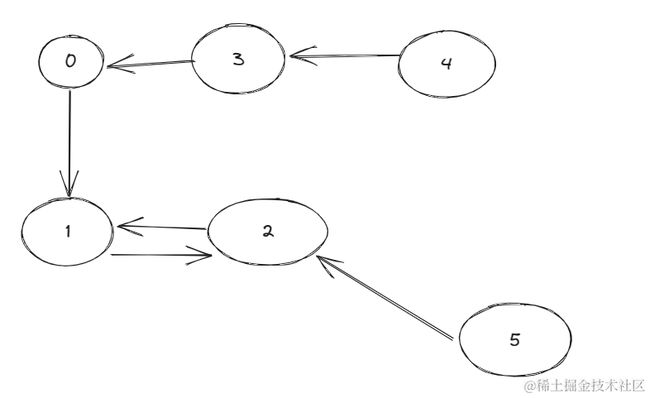
但是如果是这种情况呢:
因此本题我们需要求得最大的圆环长度以及这种彼此喜欢的环的长度以及它俩的链路长度中的最大值。
但是理解了这个题在代码实现也很麻烦~图论真的难啊
代码:
func maximumInvitations(favorite []int) int {
n := len(favorite)
deg := make([]int, n)
for _, f := range favorite {
deg[f]++ // 统计基环树每个节点的入度
}
rg := make([][]int, n) // 反图
q := []int{}
for i, d := range deg {
if d == 0 {
q = append(q, i)
}
}
for len(q) > 0 { // 拓扑排序,剪掉图上所有树枝
x := q[0]
q = q[1:]
y := favorite[x] // x 只有一条出边
rg[y] = append(rg[y], x)
if deg[y]--; deg[y] == 0 {
q = append(q, y)
}
}
// 通过反图 rg 寻找树枝上最深的链
var rdfs func(int) int
rdfs = func(x int) int {
maxDepth := 1
for _, son := range rg[x] {
maxDepth = max(maxDepth, rdfs(son)+1)
}
return maxDepth
}
maxRingSize, sumChainSize := 0, 0
for i, d := range deg {
if d == 0 {
continue
}
// 遍历基环上的点
deg[i] = 0 // 将基环上的点的入度标记为 0,避免重复访问
ringSize := 1 // 基环长度
for x := favorite[i]; x != i; x = favorite[x] {
deg[x] = 0 // 将基环上的点的入度标记为 0,避免重复访问
ringSize++
}
if ringSize == 2 { // 基环长度为 2
sumChainSize += rdfs(i) + rdfs(favorite[i]) // 累加两条最长链的长度
} else {
maxRingSize = max(maxRingSize, ringSize) // 取所有基环长度的最大值
}
}
return max(maxRingSize, sumChainSize)
}
周四:2103. 环和杆(easy)
题目描述:
总计有 n 个环,环的颜色可以是红、绿、蓝中的一种。这些环分别穿在 10 根编号为 0 到 9 的杆上。
给你一个长度为 2n 的字符串 rings ,表示这 n 个环在杆上的分布。rings 中每两个字符形成一个 颜色位置对 ,用于描述每个环:
- 第
i对中的 第一个 字符表示第i个环的 颜色('R'、'G'、'B')。 - 第
i对中的 第二个 字符表示第i个环的 位置,也就是位于哪根杆上('0'到'9')。
例如,"R3G2B1" 表示:共有 n == 3 个环,红色的环在编号为 3 的杆上,绿色的环在编号为 2 的杆上,蓝色的环在编号为 1 的杆上。
找出所有集齐 全部三种颜色 环的杆,并返回这种杆的数量。
示例 1:
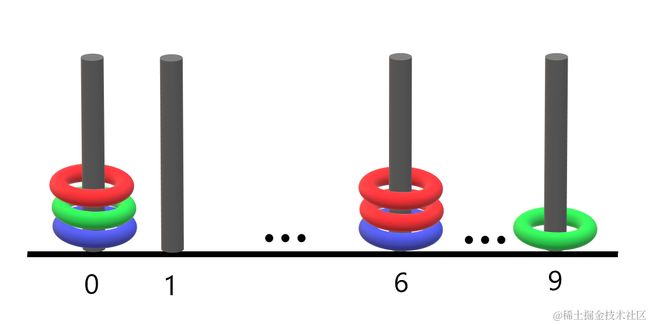
输入: rings = "B0B6G0R6R0R6G9"
输出: 1
解释:
- 编号 0 的杆上有 3 个环,集齐全部颜色:红、绿、蓝。
- 编号 6 的杆上有 3 个环,但只有红、蓝两种颜色。
- 编号 9 的杆上只有 1 个绿色环。
因此,集齐全部三种颜色环的杆的数目为 1 。
复盘:
此题就轻松很多,也没啥好说了,就遍历rings做处理,记录维护在数组,然后再遍历数组拿到符合要求的个数
代码:
func countPoints(rings string) (ans int) {
d := ['Z']int{'R': 1, 'G': 2, 'B': 4}
mask := [10]int{}
for i, n := 0, len(rings); i < n; i += 2 {
c := rings[i]
j := int(rings[i+1] - '0')
mask[j] |= d[c]
}
for _, x := range mask {
if x == 7 {
ans++
}
}
return
}
周五:117. 填充每个节点的下一个右侧节点指针 II(middle)
题目描述:
给定一个二叉树:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL 。
初始状态下,所有 next 指针都被设置为 NULL 。
示例 1:
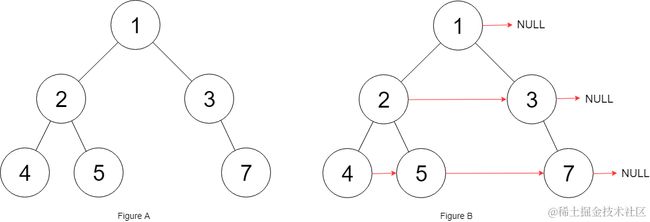
输入:root = [1,2,3,4,5,null,7]
输出: [1,#,2,3,#,4,5,7,#]
解释: 给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化输出按层序遍历顺序(由 next 指针连接),'#' 表示每层的末尾。
复盘:
显然该题应该进行层序遍历,依次对每层节点进行next连接,如果每层使用数组去维护是比较容易的,但空间复杂度为O(n),但是如果我们只维护一个哨兵节点,那就不需要额外的空间维护一整层的节点。
代码:
func connect(root *Node) *Node {
cur:=root
// cur -> bfs
for cur!=nil{
dumpNode:=&Node{}
tmp:=dumpNode
// dumpNode作为哨兵存储下次需要bfs的层级头节点
// tmp去进行next连接
for cur!=nil{
if cur.Left!=nil{
tmp.Next=cur.Left
tmp=tmp.Next
}
if cur.Right!=nil{
tmp.Next=cur.Right
tmp=tmp.Next
}
cur=cur.Next //前往当前层下个节点进行连接
}
cur=dumpNode.Next
}
return root
}
周六:421. 数组中两个数的最大异或值(middle)
题目描述:
给你一个整数数组 nums ,返回 **nums[i] XOR nums[j] 的最大运算结果,其中 0 ≤ i ≤ j < n 。
示例 1:
输入: nums = [3,10,5,25,2,8]
输出: 28
解释: 最大运算结果是 5 XOR 25 = 28.
复盘:
此题看似容易实则暗藏玄机,如果对位运算的题没这么熟悉,那可能会一头雾水,比如我。。
此题我们应当从高位到低位一步一步枚举看每一位是否可以为1,始终维护一个答案,起初为0,从高位到低位一步一步枚举看是否可以为1得出最后结果。最重要的一步是我们取一个变量newAns将我们要枚举的位先假设为1,再枚举nums的数值去进行异或,由于a^b=c–> c^b=a c^a=b这个特性我们可以通过hash去存储a的值看b是否存在,若存在显然该位可以为1
代码:
func findMaximumXOR(nums []int) (ans int) {
highBit := bits.Len(uint(slices.Max(nums))) - 1
seen := map[int]bool{}
mask := 0
for i := highBit; i >= 0; i-- { // 从最高位开始枚举
clear(seen)
mask |= 1 << i
newAns := ans | 1<<i // 这个比特位可以是 1 吗?
for _, x := range nums {
x &= mask // 低于 i 的比特位置为 0
if seen[newAns^x] { // a^b=c--> c^b=a c^a=b
ans = newAns // 这个比特位可以是 1
break
}
seen[x] = true
}
}
return
}
周日:187. 重复的DNA序列(middle)
题目描述:
DNA序列 由一系列核苷酸组成,缩写为 'A', 'C', 'G' 和 'T'.。
- 例如,
"ACGAATTCCG"是一个 DNA序列 。
在研究 DNA 时,识别 DNA 中的重复序列非常有用。
给定一个表示 DNA序列 的字符串 s ,返回所有在 DNA 分子中出现不止一次的 长度为 10 的序列(子字符串)。你可以按 任意顺序 返回答案。
示例 1:
输入: s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
输出: ["AAAAACCCCC","CCCCCAAAAA"]
复盘:
感觉其实应该是简单题,没啥好说的,枚举就行了
代码:
func findRepeatedDnaSequences(s string) (ans []string) {
cnt := map[string]int{}
for i := 0; i < len(s)-10+1; i++ {
t := s[i : i+10]
cnt[t]++
if cnt[t] == 2 {
ans = append(ans, t)
}
}
return
}
下面这题是我刷面试经典题目不会写的题,复盘加深印象
面试top150 题目收录:399. 除法求值(middle)
题目描述:
给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件,其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。
另有一些以数组 queries 表示的问题,其中 queries[j] = [Cj, Dj] 表示第 j 个问题,请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。
返回 所有问题的答案 。如果存在某个无法确定的答案,则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串,也需要用 -1.0 替代这个答案。
注意: 输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况,且不存在任何矛盾的结果。
注意: 未在等式列表中出现的变量是未定义的,因此无法确定它们的答案。
示例 1:
输入: equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
输出: [6.00000,0.50000,-1.00000,1.00000,-1.00000]
解释:
条件:a / b = 2.0, b / c = 3.0
问题:a / c = ? , b / a = ? , a / e = ? , a / a = ? , x / x = ?
结果:[6.0, 0.5, -1.0, 1.0, -1.0 ]
注意:x 是未定义的 => -1.0
复盘:
这个题如果不知道要转换成图去做真的就是一头雾水,起初我感觉可以用并查集,但是这玩意是有权值的,因此我去看答案,然后确实有带权并查集的解法,但是感觉可能我脑子确实不行,看了一两个小时,依然没弄懂到底是怎么去压缩权值的,太难了。。。。。。。
但是其实这个题其实可以转换成带权的有向图再通过bfs去查找两点间的权值和,那就会轻松很多~~~
代码:
func calcEquation(equations [][]string, values []float64, queries [][]string) []float64 {
// 给方程组中的每个变量编号
id := map[string]int{}
for _, eq := range equations {
a, b := eq[0], eq[1]
if _, has := id[a]; !has {
id[a] = len(id)
}
if _, has := id[b]; !has {
id[b] = len(id)
}
}
// 建图
type edge struct {
to int
weight float64
}
graph := make([][]edge, len(id))
for i, eq := range equations {
v, w := id[eq[0]], id[eq[1]]
graph[v] = append(graph[v], edge{w, values[i]})
graph[w] = append(graph[w], edge{v, 1 / values[i]})
}
bfs := func(start, end int) float64 {
ratios := make([]float64, len(graph))
ratios[start] = 1
queue := []int{start}
for len(queue) > 0 {
v := queue[0]
queue = queue[1:]
if v == end {
return ratios[v]
}
for _, e := range graph[v] {
if w := e.to; ratios[w] == 0 {
ratios[w] = ratios[v] * e.weight
queue = append(queue, w)
}
}
}
return -1
}
ans := make([]float64, len(queries))
for i, q := range queries {
start, hasS := id[q[0]]
end, hasE := id[q[1]]
if !hasS || !hasE {
ans[i] = -1
} else {
ans[i] = bfs(start, end)
}
}
return ans
}
总结
本周的题目图相关的题相对多,整体难度都是偏高的感觉,我的感觉是要是每道题都能AC,其实面试基本没有题目能难倒你了~~