Acwing算法基础课第二讲——数据结构

模拟单链表

方法：两个数组，一个存该索引位置的 val ， 另一个存该索引位置的下一位置（即下一个位置的索引是啥）。
其中，第0号位置仅表示 链表的 head，不进行使用。

#include 

using namespace std;
const int N = 1e5+10;
int val[N], nextA[N], len, head;
// 向第k个元素后插入一个节点x
void insert(int k,int x){
    val[len] = x;
    nextA[len] = nextA[k];
    nextA[k] = len;
    ++len;
}
// 删除第k个节点
void delet(int k){
    nextA[k] = nextA[ nextA[k] ];
}
// 遍历这个单链表
void traval(){
    int cur = nextA[head];
    while(cur != -1){
        cout << val[cur] << ' ';
        cur = nextA[cur];
    }
}

int main(){
    int n; cin >> n; cin.get();
    // 对链表的初始化
    head = 0; len = 1; nextA[head] = -1;
    for(int i = 0; i < n; ++i){
        char oper; int x, y;
        oper = cin.get();
        if(oper == 'H'){
            cin >> x; cin.get();
            insert(0,x);
        }
        else if(oper == 'I'){
            cin>> x >> y; cin.get();
            insert(x, y);
        }
        else{
            cin >> x; cin.get();
            delet(x);
        }
    }
    traval();
    
}

模拟双向链表

思路同模拟单链表，只是这里需要两个数组来存指针，并且在删点、加点的操作上有些许区别。
双链表把数组的0位置作head，1e5+3位置 ( 其实可以随意 ) 作tail。

#include 
using namespace std;

const int N = 1e5 + 10;
int val[N], pre[N], nxt[N], len, head, tail;

void init(){
    head = 0; tail = 1e5+3;
    pre[head] = -1; nxt[head] = tail;
    pre[tail] = head; nxt[tail] = -1;
    len = 1;
}

void insert(int k, int v){
    val[len] = v;
    pre[len] = k;
    nxt[len] = nxt[k];
    pre[nxt[k]] = len;
    nxt[k] = len;
    ++len;
}

void delet(int k){
    nxt[pre[k]] = nxt[k];
    pre[nxt[k]] = pre[k];
}

void traval(){
    int cur = nxt[head];
    while(cur != tail){
        cout<<val[cur]<<' ';
        cur = nxt[cur];
    }
    cout<<endl;
}

int main(){
    int m; cin>>m;
    string oper; int x, y;
    init();
    for(int i = 0 ; i < m ; ++ i){
        cin>>oper;
        if(oper == "R"){
            cin>>x;
            insert(pre[tail],x);
        }
        else if(oper == "L"){
            cin>>x;
            insert(head,x);
        }
        else if(oper == "D"){
            cin>>x;
            delet(x);
        }
        else if(oper == "IL"){
            cin>>x>>y;
            insert(pre[x],y);
        }
        else if(oper == "IR"){
            cin>>x>>y;
            insert(x,y);
        }
    }
    traval();
}

模拟栈

这里我把栈写成了一个 类 ，可能和STL没什么区别，但这里是直接开一个很大的数组，在数组上进行操作，时间上应该会更快一点。

#include 

using namespace std;
const int N = 1e5+10;
int d[N];
class myStack{
public:
    int a[N];
    int len;
    myStack(){
        len = 0;
    }
    void push(int x){
        a[len++] = x;
    }
    bool empty(){
        return len == 0;
    }
    void pop(){
        --len;
    }
    int top(){
        return a[len-1];
    }
};

模拟队列

模拟队列的缺陷就在于，当从队头pop元素后，那么这个数组的这部分就永远不会再被使用，如果操作过多，到最后队列的空间就会变成0。
解决方式是，把数组写成循环的。（还没写…）

#include 

using namespace std;

const int N = 1e5+10;
int head, tail, a[N];
void init(){
    head = 0;
    tail = 0;
}
// 向队尾插入元素
void push(int x){
    a[tail++] = x;
}
// 弹出队头元素
void pop(){
    head++;
}
// 查询队列是否为空
bool empty(){
    return head == tail;
}
// 查询队头元素
int query(){
    return a[head];
}

单调栈问题

单调栈是用来求数组中，离第 i 个数最近并大于 / 小于它的数。如[1 3 2]，离 2 最近的小于2的是1。
单调栈用一个栈来维护一个递减 / 递增序列。
如[3 4 2 7 5]，
初始时，栈为空，则比3小的为-1，然后3入栈 【3】
3比4小，则比4小的就是3，然后4入栈 【3 4】
4比2大，弹出，3比2大，弹出，没了，那就是-1，然后2入栈 【2】，这里一直弹出是因为，现在来了一个更小的，那么在后续的遍历过程中，前面的3、4都没用了，因为2比他们更小。
直到结束

#include 

using namespace std;
const int N = 1e5+10;
int d[N];
class myStack{
public:
    int a[N];
    int len;
    myStack(){
        len = 0;
    }
    void push(int x){
        a[len++] = x;
    }
    bool empty(){
        return len == 0;
    }
    void pop(){
        --len;
    }
    int top(){
        return a[len-1];
    }
};

int main(){
    int n; cin >> n;
    myStack s;
    for(int i = 0 ; i < n ; ++ i){
        cin >> d[i];
        while(!s.empty() && s.top() >= d[i]) s.pop();
        cout<< ( s.empty()?-1:s.top()) << ' ';
        s.push(d[i]);
    }
}

单调双端队列 / 滑动窗口问题

单调双端队列 能解决一个滑动窗口内 最大 / 小 值的问题。

#include 

using namespace std;

const int N = 1e6+10;

int a[N],mx[N],mn[N];
int mxhead=0,mxtail=0,mnhead=0,mntail=0;

int main(){
    int n,k; cin >> n >> k;
    for(int i = 0; i< n ; ++i) cin >> a[i];
    for(int i = 0; i < n ; ++ i){
        // 处理滑窗中的最小值，单调双端队列降序
        // 将i从队尾加入
        while(mxhead < mxtail && a[mx[mxtail-1]] >= a[i]) mxtail--;
        mx[mxtail++] = i;
        // 判断滑窗大小是否超限
        while(mx[mxhead] < i-k+1 ) mxhead++;
        // 输出队头，这里的判断是，前几次添加的时候滑窗还没满，不能输出
        if(i >= k-1) cout << a[mx[mxhead]]<<' ';
    }
    cout<<endl;
    for(int i = 0; i < n ; ++i){
        // 处理滑窗中的最大值，单调双端队列升序
        // 将 i 从队尾加入
        while(mnhead < mntail && a[mn[mntail-1]] <= a[i]) mntail--;
        mn[mntail++] = i;
        // 判断滑窗大小是否超限
        while(mn[mnhead] < i-k+1 ) mnhead++;
        // 输出队头，这里的判断是，前几次添加的时候滑窗还没满，不能输出
        if(i >= k-1) cout << a[mn[mnhead]]<<' ';
    }
}

KMP 字符串匹配问题

现有一个目标字符串 s 和 模式串 p， 找s中是否存在子串p，并返回位置。
正常暴力做法的时间复杂度是$O(N^2)$，通过KMP方法可以将复杂度降低到$O(N)$。
KMP算法是通过维护模式串 p 的一个next数组，来实现对匹配过程的加速，相当于利用上了之前的匹配信息。

以 s = aaaaaaaaaab p = aaab 为例：

next数组维护的是，p中第 i 为之前的最大前后缀匹配长度，其中对next数组，人为规定next[0] = -1 , next[1] = 0;

最大前后缀匹配长度指的是，使前k个字符的子串 和 后k个字符的子串 相等 的最大k值。如 abab，前缀2为ab，后缀2为ab，前缀3为aba，后缀3为bab，所以abab的最大前后缀匹配长度为2。

所以next[i] 表示的就是0 ~ i - 1 的子串 的最大前后缀匹配长度。

那么next数组有什么用呢？

如何快速求 next 数组：
如果暴力地求next数组，时间复杂度还是很高的——$O(N^2)$。

代码中是输出所有的匹配字符串，这和 找到一个匹配的就break有略微不同。
只要区别在：
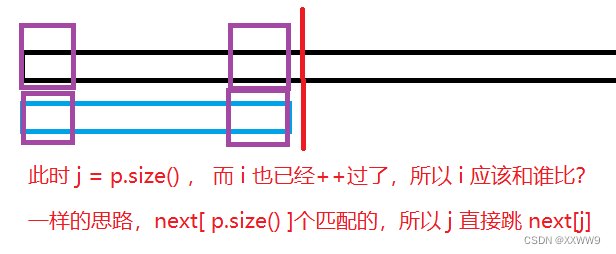
1、求模式串p 的next数组时，多求一次，把next[ p.size() ] 也求出来，表示整个串 p 的最大前后匹配长度。
2、见程序kmp函数while循环的最后一行。如果 j == p.size()， 说明已经匹配完了，push结果，同时，我们就可以通过
next[ p.size() ]来快速定位到待匹配字符。

#include 
#include 
using namespace std;

const int N = 1e5+10;
int nxt[N];

void getNxt(string & patten){
    nxt[0] = -1, nxt[1] = 0;
    int preIdx = 0, i = 2;
    while( i <= patten.size()){
        if(patten[preIdx] == patten[i-1]) nxt[i++] = ++preIdx;
        else if(preIdx != 0) preIdx = nxt[preIdx];
        else nxt[i++] = 0;
    }
}

vector<int> kmp(string & str, string & patten){
    vector<int> res;
    int i = 0, j = 0;
    getNxt(patten);
    while( i < str.size()){
        if(str[i] == patten[j]) ++i, ++j;
        else if(j == 0) ++i;
        else  j = nxt[j];
        if(j == patten.size()) res.push_back(i-patten.size()) , j = nxt[j];
    }
    return res;
}

int main(){
    string a,b;
    int tp;
    cin >> tp >> a >> tp >> b;
    vector<int> idxs = kmp(b, a);
    for(auto x : idxs){
        cout<< x << ' ';
    }
    cout << endl;
    
}

Trie树 / 前缀树

这个的思路我是按照牛客算法班的思路来写的。 没有考虑内存的释放问题，只开new数组，不管释放。

并且，如果把Trie树封装成一个类，会增加运算时间，所以这里用数组来模拟Trie树类的操作。

首先是，，一个index[N][26]数组来存所有的Trie树节点，同时里面的值是下一个位置的行索引。
一个pass[N][26]数组来存储经过节点的次数， 一个end[N][26]数组来存储终止于节点的次数。

在插入到某个字母的时候，如果当前没有，就把新节点放在index的len位置，同时该节点的idx指向len位置。

#include 

using namespace std;

const int N = 1e5;
int idx[N][27], pass[N][27], ed[N][27], len;
void insert(const string & s){
    int slen = s.size(), row = 0;
    for(int i = 0; i != slen; ++ i){
        if(idx[row][s[i]-'0'] == 0) idx[row][s[i]-'0']=++len;
        pass[row][s[i]-'0'] ++;
        if(i == slen-1) ed[row][s[i]-'0']++;
        row = idx[row][s[i]-'0'];
    }
}

int query(const string & s){
    int res = 0;
    int slen = s.size(), row = 0;
    for(int i = 0; i != slen; ++ i){
        if(idx[row][s[i]-'0'] == 0) return res;
        if(i == slen-1) res = ed[row][s[i]-'0'];
        row = idx[row][s[i]-'0'];
    }
    return res;
}

int main(){
    len = 0;
    int t; cin >> t; cin.get();
    for(int i = 0 ; i < t ; ++ i){
        char ord = cin.get();
        string s; cin >> s; cin.get();
        if(ord == 'Q'){
            cout<< query(s) << endl;
        }
        else{
            insert(s);
        }
    }
}

Trie树的应用 最大异或对

这样的问题可以被抽象成 Trie树问题。
将一个数表示成二进制的形式，那么第 i 位的值就只有两种情况：0 和 1
所以这可以看成idx[N][2] 的Trie树。
首先把所有的数都插入到Trie树中。
然后再依次遍历，因为找的是最大异或对，那么如果Trie树种存在 和 自己每一位的 非 都相同的数，则和这个数异或后就能得到全1的数字，也就最大了。所以我们的查询目标就是找自己的反码。
如果某一位没有找到自己的反码，如 自己的是1，但是没找到0，那就退而求其次，这一位用1代替。

#include 

using namespace std;

const int N = 1e5+10;
int dd[N], nxt[31*N][2];
int idx;

void insert(int aa){
    int p = 0;
    for(int i = 30; i >=0 ; -- i){
        int & target = nxt[p][(aa>>i) & 1];
        if(target == 0) target = ++idx;
        p = target;
    }
}

int query(int x){
	//输入是x，但找的是x的反码
    int res = 0, p = 0;
    for(int i = 30; i >=0 ; -- i){
        int & target = nxt[p][!((x>>i) & 1)];
        if(target != 0){
            res+=(1<<i);
            p = target;
        }
        else p = nxt[p][(x>>i) & 1];
    }
    return res;
}

int main(){
    int n; cin >> n;
    idx = 0;
    for(int i = 0 ; i < n ; ++ i) {
        cin >> dd[i];
        insert(dd[i]);
    }
    int res = 0;
    for(int i = 0 ; i < n ; ++ i){
        res = max(res, query(dd[i]));
    }
    cout<< res ;
}

并查集

数组方式实现的并查集，带有优化。
通过父节点来表示其所属的组，如果父节点仍有父节点，则节点所属的组应是递归的父节点，若父节点就是本身，则组的编号就是本身。
首先，一个数组fa[N]标记当前节点的父节点是谁，然后一个num[N]数组来表示以 i 为编号的组内有多少个成员。（成员对应的num[i]为0）。最初时，fa[N]中每个点都指向自己，同时num中都是1。
然后合并某些节点时，将某个组的组号的父指向另外一个节点，同时将num相加， 就能实现合并。

#include 
using namespace std;

const int N = 1e5+10;
int fa[N], num[N];

void init(){
    int n; cin >> n;
    for(int i = 1 ; i <= n ; ++ i){
        fa[i] = i;
        num[i] = 1;
    }
}
int findfa(int x){
	// 递归查询，这样就能实现对fa数组的优化，避免链状查询过久的情况
    if(fa[x] != x) fa[x] = findfa(fa[x]);
    return fa[x];
}
bool sameset(int a, int b){
    return findfa(a) == findfa(b);
}
void uniontwo(int a,int b){
    int ffa = findfa(a), ffb = findfa(b);
    if(ffa == ffb) return;
    num[ffa] += num[ffb];
    num[ffb] = 0;
    fa[ffb] = ffa;
    
}
int getnum(int x){
    return num[findfa(x)];
}

int main(){
    init();
    int m; cin >> m; cin.get();
    while(m--){
        string ope;int x, y;
        cin>>ope;
        if(ope == "C"){
            cin >> x >> y; cin.get();
            uniontwo(x, y);
        }
        else if(ope == "Q1"){
            cin >> x >> y; cin.get();
            cout<< ( sameset(x, y)?"Yes":"No" ) << endl;
        }
        else{
            cin >> x; cin.get();
            cout<< getnum(x) << endl;
        }
    }
}

模拟堆

用数组模拟小根堆，堆中一个节点（从1开始存储，0位置不存数据）的父节点是 x / 2 ，左子树为 x * 2 ，右子树为 x * 2 + 1。

up(int x)函数：将第x位置的值向上传递。
当没有越界 且 当前位置的值比父节点小的时候，交换当前节点和父节点的值，然后 当前节点 = 父节点。

down(int x)函数：将x位置的值向下传递。
首先，最子树根 = 当前节点
第一次：当没有越界 且 最小子树的值比左子树大的时候，最小子树= 左子树。
第二次：当没有越界 且 最小子树的值比右子树大的时候，最小子树 = 右子树。
如果最小子树更新了（即，最小子树 ≠ 当前节点） 交换位置，递归到最小子树。

heapfy函数：将整个堆进行排序，使之成为小根堆
从下往上，从len/2的位置开始down( i )，因为叶子节点不需要down

/*  堆排序的算法  */
#include 
 
using namespace std;
 
const int N = 1e5+10;
int hp[N], len;
void up(int idx){
    int cur = idx, par = (cur-1)/2;
    while(cur>0 && hp[cur] < hp[par]){
        swap(hp[cur],hp[par]);
        cur = par;
        par = (cur-1)/2;
    }
}
void down(int idx){
    int cur = idx, chd = cur;
    if(2*cur+1 < len && hp[cur] > hp[2*cur+1]) chd = 2*cur+1;
    if(2*cur+2 < len && hp[chd] > hp[2*cur+2]) chd = 2*cur+2;
    while(cur != chd){
        swap(hp[cur], hp[chd]);
        cur = chd;
        if(2*cur+1 < len && hp[cur] > hp[2*cur+1]) chd = 2*cur+1;
        if(2*cur+2 < len && hp[chd] > hp[2*cur+2]) chd = 2*cur+2;
    }
}
int main(){
    len = 0;
    int n,m ; cin >> n >> m;
    for(int i = 0; i < n ; ++ i){
        cin >> hp[i];
        len++;
    }
    for(int i = len/2; i>=0 ; --i) down(i);
    for(int i = 0 ; i < m ; ++i){
        cout<< hp[0] << ' ';
        hp[0] = hp[--len];
        down(0);
    }
}

一个考脑筋急转弯，索引转换的题。

这个题比较难理解的是，怎么去映射 输入的顺序 —— 排序后的顺序
这里是用了两个数组 heap2order[] 和 order2heap[] 来存储 堆 -> 输入 和 输入 -> 堆的映射
在heap_swap(int x , int y)函数中，要想交换堆中的 x 位置 和 y 位置的两个数据，如图所示

我们已知的是，x 和 y 那么我们不怕丢失的就是指向 x 和 指向 y 的索引。
所以，我们应该先交换 swap(order2heap[heap2order[x]] , order2heap[heap2order[y]] )
然后再交换 swap( heap2order[ x ] , heap2order[ y ] ) 。
然后交换heap中的值。（值的交换顺序无所谓）

#include 

using namespace std;

const int N = 1e5+10;
int heap[N], heap2order[N], order2heap[N];
int heapSize, insertTime;

void heap_Swap(int a, int b){
    // 交换heap中 a , b 索引的值
    swap(heap[a], heap[b]);
    swap(order2heap[heap2order[a]] , order2heap[heap2order[b]]);
    swap( heap2order[a], heap2order[b] );
}

void up(int x){
    int par = x/2;
    while(x != 1 && heap[x] < heap[par]){
        heap_Swap(x,par);
        x = par; par = x/2;
    }
}
void down(int x){
    int chd = x;
    if(2*x <= heapSize) chd = heap[2*x]<heap[x]?2*x:chd;
    if(2*x+1 <= heapSize) chd = heap[2*x+1]<heap[chd]?2*x+1:chd;
    while(chd != x){
        heap_Swap(x,chd);
        x = chd;
        if(2*x <= heapSize) chd = heap[2*x]<heap[x]?2*x:chd;
        if(2*x+1 <= heapSize) chd = heap[2*x+1]<heap[chd]?2*x+1:chd;
        // down(chd);
    }
}

int main(){
    heapSize = 0, insertTime = 0;
    
    int n; cin >> n;
    while(n--){
        string ope; cin >> ope;
        if(ope == "I"){
            int x; cin >> x;
            ++heapSize; ++insertTime;
            heap[heapSize] = x;
            order2heap[insertTime] = heapSize;
            heap2order[heapSize] = insertTime;
            up(heapSize);
        }
        else if(ope == "PM"){
            cout<<heap[1]<<endl;
        }else if(ope == "DM"){
            heap_Swap(1,heapSize);
            heapSize--;
            down(1);
        }
        else if(ope == "D"){
            int x; cin >> x;
            x = order2heap[x];
            heap_Swap(x,heapSize);
            heapSize--;
            up(x);
            down(x);
            
        }else{
            int x, val; cin >> x >> val;
            x = order2heap[x];
            //heap_Swap(x,heapSize);
            heap[x] = val;
            up(x);
            down(x);
        }
    }
    
    return 0;
}

模拟散列表（Hash）

数组哈希

1、开放寻址法

首先确定 hash函数，即把数值映射到一个hash表中的某个索引。
如果定义哈希函数为1e5+3，则应设置哈希表大小为 2*1e5+3，保证数据能存下来。
然后，将哈希表中的值进行初始化为0x3f3f3f3f，来表示这个位置有没有存储数据。
开放寻址法就是，如果求出的位置有数据在了，就向下一个位置放，如果还有数据，就接着往下找，如果到末尾了，就重新回到0，形成一个循环数组，直到放下。

因为输入的数字有可能是小于0的负数，所以需要 （X%MOD + MOD) % MOD。

#include 
#include 
using namespace std;
// 开放寻址法
const int N = 2*1e5+10, null = 0x3f3f3f3f;
const int MOD = 100003;

int hasharr[ N ];

int hashfunc(int x){
    return ( x % MOD + MOD)%MOD;
}

void insert(int x){
    int idx = hashfunc(x);
    while(hasharr[idx] != null){
        ++idx;
        if(idx == N) idx = 0;// 必须形成循环数组
    }
    hasharr[ idx ] = x;
}
bool query(int x){
    int idx = hashfunc(x);
    while(hasharr[idx] != x && hasharr[idx]!= null) {
        ++idx;
        if(idx == N) idx = 0;
    }
    if(hasharr[idx] == x) return 1;
    return 0;
}

int main(){
    memset(hasharr,0x3f,sizeof hasharr);
    int n; cin >> n; cin.get();
    while(n--){
        string  ope ;
        int x;
        cin >> ope;
        // cout<< ope << endl;
        if(ope == "I"){
            cin >> x;
            insert(x);
        }
        else{
            cin >> x;
            cout<< (query(x)?"Yes":"No") << endl;
        }
    }
}

2、拉链法

拉链法 用一个hasharr来存储每个位置的链表头，每个位置是一个链表，哈希出来是这个位置的值都被挂在这个链上，
然后用一个val[] 和一个 nxt[] 数组来存储 哈希的值 和下一个位置的索引。

#include 
#include 
using namespace std;
// 拉链法
const int N = 1e5 + 10, MOD = 1e5, null = 0x3f3f3f3f;
int hasharr[N];
int len, val[N], nxt[N];

int hashfunc(int x){
    return (x % MOD + MOD) % MOD;
}
void insert(int x){
    int idx = hashfunc(x);
    // 头插法，直接插在head
    val[++len] = x;
    nxt[len] = hasharr[idx];
    hasharr[idx] = len;
}
bool query(int x){
    int idx = hashfunc(x);
    int cur = hasharr[idx];
    while(cur != -1 && val[cur]!=x) cur = nxt[cur];
    if(cur == -1) return 0;
    return 1;
}
int main(){
    len = 1;
    memset(hasharr, -1 , sizeof hasharr);
    int n; cin >> n;
    while(n--){
        string ope; cin >> ope;
        int x; cin >> x;
        if(ope == "I") insert(x);
        else cout<< (query(x)?"Yes":"No") << endl;
    }
}

字符串哈希

字符串哈希用一个p值，Q值 以及 字符的ASCII码来表示一个字符串。
首先是一个unsigned long long 数组 h[] 来存储每个的结果
然后从字符串的第0位开始，h[]需要从第一位开始，h[ i ] = （h[ i - 1 ] *p + s[ i - 1 ]）% Q
这样就相当于搞了一个字符串的前缀数组。

当我们需要查找某个位置 L ~ R 的字符串时，因为L之前可能有字符，记为h[L-1]，则如果想把L ~ R当成从0开始的字符串，应该去掉h[L-1]的干扰，公式为：h[R] - h[L-1]*$p^{R-L+1}$ % Q，这样得到的结果就是L ~ R 子串的哈希编码了。
如果两个子串的哈希编码相同，则子串就相同。（当p取131、13331的时候，Q取$2^{64}$的时候，冲突的概率极小，而unsigned long long 刚好能对较大的数进行截断，就相当于对Q取模了。

#include 
using namespace std;
const int N = 1e5+10;
int p = 131;
unsigned long long h[N],pows[N];
string s;

unsigned long long getHash(int ll, int rr){
    unsigned long long res = 0;
    res = h[rr] - h[ll-1]*pows[rr-ll+1];
    return res;
}


int main(){
    int n, m; cin >> n >> m;
     cin >> s;
     pows[0]=1;
    for(int i = 1; i <= n; ++ i){
        pows[i] = pows[i-1]*p;
        h[i] = h[i-1]*p + s[i-1];
    }
    while(m--){
        int ll, rr, lll, rrr; cin >> ll >> rr >> lll >> rrr;
        if(getHash(ll,rr) == getHash(lll,rrr)){
            cout<<"Yes"<<endl;
        }
        else{
            cout<<"No"<<endl;
        }
    }
}