Leetcode链表篇总结(C++)
文章目录
- 一、基础知识
- 二、经典题目
-
- 1、 203:移除链表元素(简单)
- 2、707-设计链表(中等)
- 3、206-反转链表(简单)
- 4、142-环形链表(中等)
- 5、19-删除链表的倒数第N个结点(中等)
- 6、面试题 02.07. 链表相交(简单)
- 三、总结
-
- 1、链表的处理通常考虑添加虚拟节点来简化逻辑操作
- 2、常见数值范围与对应十进制数值
注:按照代码随想录的刷题指南进行,自己总结补充,以加深印象
参考链接:https://leetcode-cn.com/circle/article/wGp7Y9/
题目来源:力扣(LeetCode)
一、基础知识
1、链表的定义
单链表:(leetcode上的实现)
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
其中不定义构造函数也可以,但c++默认的构造函数并不能初始化任何成员值,需要new之后额外赋值。
2、存储方式
在内存中并不会额外存储
3、分类
单链表,双链表,循环链表
4、与数组的关系
数组:适合数据量固定、较多查询、较少增删的情况。
链表:适合数据量不固定、较少查询、较多增删的情况。
5、注意
**删除链表元素时,在C++里最好是再手动释放这个D节点,释放这块内存。**其他语言例如Java、Python,就有自己的内存回收机制,就不用自己手动释放了
二、经典题目
1、 203:移除链表元素(简单)
题目:给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点
示例:
输入:head = [1,2,6,3,4,5,6], val = 6
输出:[1,2,3,4,5]
关键点:虚拟头节点方便链表节点的删除(因为带虚拟头节点不需要再站专门对头节点的删除进行判断,逻辑简单,提交结果表明运行时间提高很大。但需注意,返回时应返回直接时的头节点位置!dummyhead->next)
复杂度:空间复杂度O(1),时间O(n)
class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
ListNode * dummyhead = new ListNode(val-1,head);//虚拟头节点
ListNode * p = dummyhead;//当前处理节点的前驱结点
ListNode *q = nullptr;
while(p->next != nullptr){
if((p->next)->val == val){
q = p->next;
p->next = p->next->next;
delete q; //释放内存
}else{
p = p->next;
}
}
return dummyhead->next;
}
解法2:递归法
基本思想: 递归法,从上到下如果当前节点不是val,则向上一层返回自己的指针;否则返回自己的后继节点的指针。
分析:时间复杂度是O(n)。递归的方法调用栈深度是n,所以空间复杂度O(n)
ListNode* removeElements(ListNode* head, int val) {
if(head == nullptr)
return nullptr;
head->next=removeElements(head->next,val);
if(head->val==val){
return head->next;
}else{
return head;
}
// 作者:lewis-dXStAbdZEw
// 链接:https://leetcode-cn.com/problems/remove-linked-list-elements/solution/203yi-chu-lian-biao-yuan-su-by-lewis-dxstabdzew/
2、707-设计链表(中等)
题目:
设计链表的实现。您可以选择使用单链表或双链表。单链表中的节点应该具有两个属性:val 和 next。val 是当前节点的值,next 是指向下一个节点的指针/引用。如果要使用双向链表,则还需要一个属性 prev 以指示链表中的上一个节点。假设链表中的所有节点都是 0-index 的。
在链表类中实现这些功能:
get(index):获取链表中第 index 个节点的值。如果索引无效,则返回-1。
addAtHead(val):在链表的第一个元素之前添加一个值为 val 的节点。插入后,新节点将成为链表的第一个节点。
addAtTail(val):将值为 val 的节点追加到链表的最后一个元素。
addAtIndex(index,val):在链表中的第 index 个节点之前添加值为 val 的节点。如果 index 等于链表的长度,则该节点将附加到链表的末尾。如果 index 大于链表长度,则不会插入节点。如果index小于0,则在头部插入节点。
deleteAtIndex(index):如果索引 index 有效,则删除链表中的第 index 个节点。
示例:
MyLinkedList linkedList = new MyLinkedList();
linkedList.addAtHead(1);
linkedList.addAtTail(3);
linkedList.addAtIndex(1,2); //链表变为1-> 2-> 3
linkedList.get(1); //返回2
linkedList.deleteAtIndex(1); //现在链表是1-> 3
linkedList.get(1); //返回3
思路:五个函数覆盖了链表的常见操作,是练习链表操作非常好的一道题目
解法1:单链表
class MyLinkedList {
//在这个类中,封装了单链表的数据结构和其上的操作
public:
struct Node{
int val;
Node * next;
Node(int val ):val(val), next(nullptr){};
Node(int val , Node* next):val(val), next(next){}
};
MyLinkedList() {
//虚拟节点方便计算
_dummyHead = new Node(0);
_maxindex = -1;
}
int get(int index) {
if(index < 0 || index >_maxindex)
return -1;
Node * cur = _dummyHead;
for(int i = 0; i <= index; i++){
cur = cur->next;
}
return cur->val;
}
void addAtHead(int val) {
Node * newNode = new Node(val, _dummyHead->next);
_dummyHead->next = newNode;
_maxindex++;
}
void addAtTail(int val) {
Node * cur = _dummyHead;
while(cur->next != nullptr){
cur = cur->next;
}
Node * newNode = new Node(val);
cur->next = newNode;
_maxindex++;
}
void addAtIndex(int index, int val) {
if(index == _maxindex +1 )
addAtTail(val);
else if(index > _maxindex+1)
return ;
else{
Node * cur = _dummyHead;
for(int i = 0 ; i < index; i++){
cur = cur->next;
}
Node * newNode = new Node(val);
newNode->next = cur->next;
cur->next = newNode;
_maxindex++;
}
}
void deleteAtIndex(int index) {
if(index < 0 || index > _maxindex)
return ;
Node * cur = _dummyHead;
for(int i = 0 ; i < index; i++){
cur = cur->next;
}
Node * p = cur->next;
cur->next = p->next;
delete p;
_maxindex--;
}
private:
int _maxindex;//链表的最大索引值
Node * _dummyHead;
};
/**
* Your MyLinkedList object will be instantiated and called as such:
* MyLinkedList* obj = new MyLinkedList();
* int param_1 = obj->get(index);
* obj->addAtHead(val);
* obj->addAtTail(val);
* obj->addAtIndex(index,val);
* obj->deleteAtIndex(index);
*/
解法2:双链表
其结构复杂,但优点是在插入节点时,可以通过比较index和index_size来判断是从头结点或者尾结点来查询;双链表同样使用虚拟头节点和虚拟尾结点来简化插入和删除。
双链表节点
struct ListNode{
int val;
ListNode* prev, * next;
}
3、206-反转链表(简单)
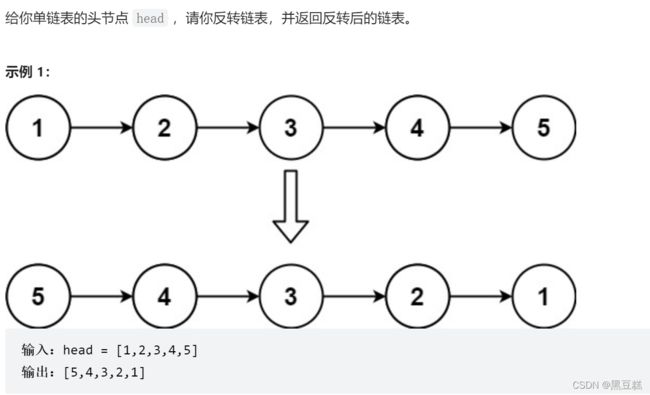
**基本思想:双指针实现,将两个节点间的link反转,**参考链接的动图https://github.com/youngyangyang04/leetcode-master/blob/master/problems/0206.%E7%BF%BB%E8%BD%AC%E9%93%BE%E8%A1%A8.md
解法1:双指针解法
注意点:
// ListNode * prev = head;
// ListNode * cur = head->next;
最开始赋值错误,cur不能直接是第二个节点,这样节点1的next没有改变,则构成了环
ListNode* reverseList(ListNode* head) {
if(head == nullptr)
return nullptr;
//赋值错误,cur不能直接是第二个节点,这样节点1的next没有改变,则构成了环
// ListNode * prev = head;
// ListNode * cur = head->next;
ListNode * cur = head;
ListNode * prev = nullptr;
ListNode * p = nullptr;
while(cur != nullptr){
p = cur->next;
cur->next = prev;
prev = cur;
cur = p;
}
return prev;
}
解法2:递归解法,逻辑同双指针
ListNode * reverse(ListNode * prev, ListNode * cur){
if(cur == nullptr)
return prev;
ListNode * p = cur->next;
cur->next = prev;
return reverse(cur, p); //最终函数结果为递归最后一层返回的值
}
ListNode* reverseList(ListNode* head) {
ListNode * cur = head;
ListNode * prev = nullptr;
return reverse(prev, cur);
}
4、142-环形链表(中等)
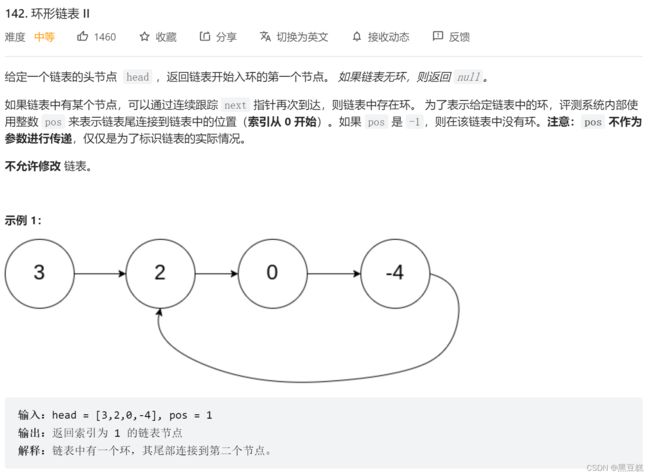
简单解法:用hash表存储每一个节点,判断是否重复;nordered_set
解法2:双指针,快指针一次两步,慢指针一次一步,如果有环,两指针一定在环中相遇
关键点:数学公式推导
1、如何判断相遇?在无环情况下,快慢指针永远不会相遇,所以相遇点一定在环上
2、为何慢指针第一圈走不完一定会和快指针相遇:当慢指针刚到达环的入口时,快指针此时在环中的某个位置,设环的周长为n,两者距离x>=0;那么看成快指针追赶慢指针,需要追赶n-x; 以慢指针为参考系,快指针相当于每次追赶1步。那么追赶需要(n-x)s ,则慢指针走的路程小于等于n,即走不完一圈就和快指针相遇
3、如何判断相遇点: 图片来自代码随想录
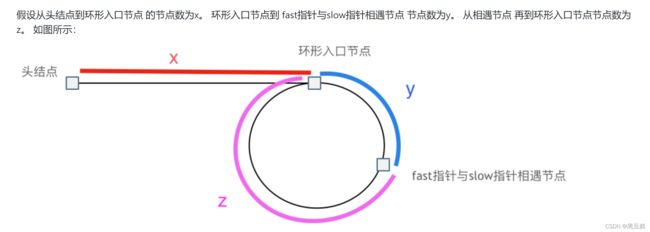
相遇时: slow 经过的节点数 x+y; fast的节点数 x + n(y+z) + y ;
2 * (x+ y ) = x + y + n(y+z),
其中n为fast指针循环的圈数,由分析2可知n = 1, 所以x = z
所以两个指针, 分别从相遇点和head节点出发,再次相遇的节点便是环的入口
代码:
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *fast, * slow;
fast = slow = head;
while(fast != NULL && fast->next != NULL){
fast = fast->next->next;//两步
slow = slow->next;
//两者相遇
if(fast == slow){
slow = head;
//根据公式x = (n-1)(y+z)+z, 从相遇点和首节点开始循环,最终相遇点为环的入口
while(slow != fast){
slow = slow->next;
fast = fast->next;
}
return slow;
}
}
return NULL;
}
};
5、19-删除链表的倒数第N个结点(中等)

思想1:首先想到用递归,在fun函数体内犯了一个错误,直接写了return a++, 那么++写在数值后面,那么返回值就都是1。官方题解里还直接用栈存储所有结点,然后再pop出去,第N个就是要删除的节点,和递归思想类似。
分析:时间复杂度O(n)
class Solution {
public:
int fun(ListNode * head, int n){
if(head->next == nullptr){
return 1;
}
int a = fun(head->next, n);
//cout<
if(a == n){
ListNode * p = head->next;
head->next = p->next;
delete p;
}
a = a + 1;
return a;
}
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode * dummyHead = new ListNode();
dummyHead->next = head;
int a = fun(dummyHead, n);
//cout<
return dummyHead->next;
}
};
思想2:双指针,如果要删除倒数第n个节点,让fast移动n步,然后让fast和slow同时移动,直到fast指向链表末尾。删掉slow的后继节点即可。
分析:只需要遍历一次,时间复杂度O(n)
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode * dummyHead = new ListNode();
dummyHead->next = head;
ListNode * fast, * low;//最终low指向倒数第N个节点的前驱节点,fast指向最后一个节点
fast = dummyHead;
low = dummyHead;
int i = 0;
while(i < n && fast != nullptr){
fast = fast->next;
i++;
}
while(fast->next != nullptr){
low = low->next;
fast = fast->next;
}
ListNode * p = low->next;
low->next = low->next->next;
delete p;
return dummyHead->next;
}
6、面试题 02.07. 链表相交(简单)
题目描述:

思路1:将两个链表从尾部对齐,指针指向两者头部对齐的位置,一齐向后遍历,查看指针是否相等
注意点: 注意边界!
分析:时间复杂度O(lenA + lenB),空间O(1)
node1 = lenA > lenB ? headA : headB;
//之前写的是lenA
node2 = lenA <= lenB ? headA : headB;
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
int lenA = 0, lenB = 0;
ListNode * node1,* node2 ;
//计算A的长度
node1 = headA;
while(node1 != NULL){
lenA++;
node1 = node1->next;
}
//计算B的长度
node1 = headB;
while(node1 != NULL){
lenB++;
node1 = node1->next;
}
//分别指向链表对齐的地方,其中node1需要提前向前
node1 = lenA > lenB ? headA : headB;
node2 = lenA <= lenB ? headA : headB;//之前写的是lenA next;
}
while(node1 != NULL && node2 != NULL){
if(node1 == node2){
return node1;
}
node1 = node1->next;
node2 = node2->next;
}
return NULL;
}
思路2:刚开始就被极短的代码量惊到了,参考链接(https://leetcode-cn.com/problems/intersection-of-two-linked-lists-lcci/solution/mian-shi-ti-0207-lian-biao-xiang-jiao-sh-b8hn/)
即nodeA遍历完A后再遍历B ; nodeB遍历B完后遍历A;如果两个链表有交点,那么必然会在第一个公共交点处相遇, 否则最终都在链表结尾null相遇。
数学原理: 设链表A的长度为a, B的长度为b, 公共长度为c
当走到第一个公共交点时,nodeA所走路径: a+ (b-c); 同理,nodeB所走路径为b+(a-c) ; 两者相等,即为相遇 a+ (b-c) = b +(a-c)
分析:时间复杂度O(lenA + lenB),空间O(1)
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode * nodeA, * nodeB;
nodeA = headA;
nodeB = headB;
while(nodeA != nodeB){
nodeA = nodeA != NULL ? nodeA->next : headB;
nodeB = nodeB != NULL ? nodeB->next : headA;
}
return nodeA;
}
思路3:用堆栈思想,从尾部开始判断,但显然空间复杂度较高O(lenA+lenB)
三、总结
1、链表的处理通常考虑添加虚拟节点来简化逻辑操作
2、常见数值范围与对应十进制数值
| 类型 | 二进制范围 | 十进制范围 |
|---|---|---|
| int | -231~(2 31-1) | 109数量级 |
| unsigned int | 0~(2 32-1) | 109数量级 |
| long int | -263~(2 63-1) | 1018数量级 |