算法：二分查找算法

查找算法

查找算法是一种用于在数据集中查找特定元素的算法。常见的查找算法包括线性查找、二分查找、哈希查找等。

1. 线性查找（Sequential Search）：逐个比较数据集中的元素，直到找到目标元素或遍历完整个数据集。
2. 二分查找（Binary Search）：对于已排序的数组，通过不断地二分划分数据集，缩小查找范围，最终找到目标元素。
3. 哈希查找（Hash Search）：利用哈希函数将元素映射到哈希表中的某个位置，并通过该位置来查找目标元素，具有较快的查询速度。
4. 插值查找（Interpolation Search）：针对有序且均匀分布的数据集，根据目标值在数据集中的相对位置，动态计算查找范围，提高查找效率。
5. 跳表（Skip List）：通过构建多层索引来加速有序链表的查找操作，类似于二分查找，但不需要对数据集进行预排序，适合于链表的查找。

这些算法各有特点，适用于不同类型的数据集和查找需求。根据具体情况选择合适的查找算法可以提高查找效率。

本文我们主要介绍二分查找。

首先，我们先来了解最基本的查找：顺序查找

顺序查找

顾名思义，顺序查找就是在一堆数据中挨个的去找某个数据

缺点：在数据量特别大的时候，顺序查找的从前往后挨个找的形式，性能是很差的。

二分查找（折半查找）

使用前提：

数据中的数据必须是有序的。

核心思想：

每次排除一半的数据。

主要步骤：

在二分查找过程中，首先确定数据集的中间元素，然后将目标元素与中间元素进行比较。如果目标元素等于中间元素，则查找成功；如果目标元素小于中间元素，则在数据集的前半部分继续查找；如果目标元素大于中间元素，则在数据集的后半部分继续查找。

通过不断地将查找范围缩小一半，最终可以在较短的时间内找到目标元素或确定目标元素不存在于数据集中。二分查找的时间复杂度为O(log n)，其中n为数据集中元素的数量。

例子：

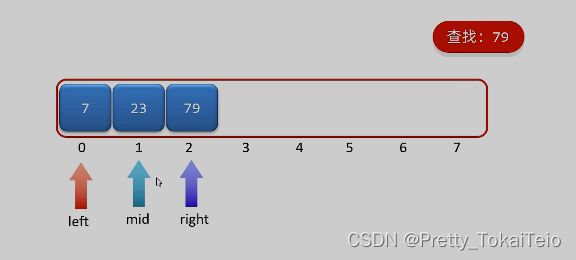
在这一组排好序的数组中查找79的数据元素

首先找到数组第一个和最后一个元素并记住他们的索引：0 和 7 ，然后找到中间元素索引 mid = (left + right) / 2折半，计算的结果为3

再然后比较索引为3的元素和目标元素的数值，发现79比81要小，说明要找的元素在mid的左边，于是中间和右边的数据要全部砍掉

此时右边位置right要变成中间位置mid-1 ， 继续进行mid = (left + right) / 2折半

然后比较79与中间位置的数据，发现79要打，所以要砍掉中间和左边的所有数据

然后left和right重后，继续折半还是这个位置，最后就找到了79。

（图片出自黑马程序员磊哥视频）

查找失败的情况：

在二分查找中，查找失败的条件是查找范围缩小到最小后仍未找到目标元素。具体表现为以下两种情况：

1. 数据集为空：如果初始的数据集为空，或者经过二分划分后查找范围为空，表示目标元素不存在于数据集中，查找失败。
2. 数据集非空但最终未找到目标元素：当查找范围缩小到只包含一个元素时，如果该元素与目标元素不相等，则表示目标元素不存在于数据集中，查找失败。
    

在这两种情况下，二分查找算法将返回一个表示查找失败的标志，通常是返回一个特殊的值（如-1）或者返回一个错误码。

结论：

二分查找正常的折半条件应该是开始位置left <= 结束位置right

代码实现（含注释）：

public static void main(String[] args) {
        //准备一个数组
        int[] arr = {7,23,79,81,103,127,131,147};

        System.out.println(binarySearch(arr, 81));
    }

    //定义二分查找的方法
    public static int binarySearch(int[] arr , int data){
        //1.定义两个变量，一个站在左边位置，一个站在右边位置
        int left = 0;
        int right = arr.length-1;

        //2.定义一个循环控制折半，因为不知道要折半多少次，所以使用while循环
        while (left <= right){
            //3.每次折半，都算出中间位置的索引
            int middle = (left + right) /2;
            //4.判断当前要找的元素值与中间位置元素值的大小情况
            if(data < arr[middle]){
                //往左边找：截止位置（右边位置） = 中间位置 - 1
                right = middle -1;
            } else if (data > arr[middle]) {
                //往右边找：起始位置（左边位置） = 中间位置 + 1
                left = middle + 1;
            }else {
                //中间位置的元素值，正好等于我们要找的元素值
                return middle;
            }
        }
        return -1;//没有找到数据
    }

另外，java中有一个方法可以实现二分查找

Arrays.binarySearch(int[] a,int k)

大家可以去看看这个的源码，与以上代码的逻辑基本相同。