Mastering the game of Go without human knowledge (AlphaGo Zero)

AlphaGo的树搜索结合了深度神经网络，这些网络是由专家知识进行监督式学习以及从selfplay中进行强化学习。AlphaGo Zero仅基于强化学习，一个神经网络被训练来预测行为的选择和价值。该神经网络提高了树搜索的性能，从而在下一次迭代中提供了更高质量的移动选择和更强的自我玩法，同时更精确的树搜索又能改善网络性能。

---

Introduction

AlphaGo训练了两个神经网络——策略网络和值网络。策略网络通过监督学习进行初始化训练，以准确预测人类专家的行动，随后通过策略梯度强化学习对其进行完善。 价值网络以预测策略网络自我博弈的赢家来进行训练。一旦经过训练，这些网络将与蒙特卡洛树搜索（MCTS）组合在一起以提供前瞻性搜索。使用策略网络将搜索范围缩小到高概率移动，并使用价值网络（与蒙特卡罗rollouts结合使用快速rollouts策略）以评估树中的位置。

AlphaGo Zero与AlphaGo不同之处在于：

• 它仅通过selfplay强化学习来训练，从随机游戏开始，无需任何监督或使用人类数据；
• 它仅使用棋盘上的黑白子作为输入特征；
• 它使用单个神经网络，而不是单独的策略和价值网络；
• 它使用了一个更简单的树搜索，该树搜索依靠此单个神经网络来评估位置和样本行为，而无需执行任何Monte Carlo rollouts操作。

为此，作者在训练循环内结合了lookahead search。

Reinforcement learning in AlphaGo Zero

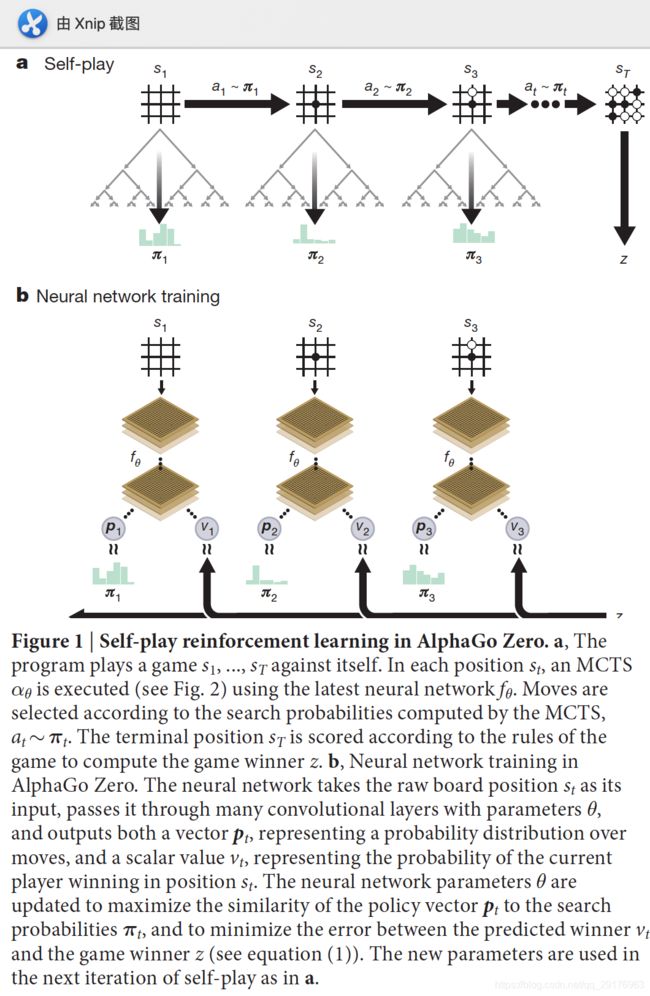
AlphaGo Zero使用参数为θ的深度神经网络$f_{\theta }$。该神经网络将位置及其历史的原始棋盘表示$s$作为输入，并输出移动概率和价值，$(\mathbf{p},v)=f_{\theta }(s)$。移动概率向量$\mathbf{p}$表示选择每个移动a（包括pass）的概率，$p_a=Pr(a|s)$。值$v$是一个标量评估，它估计当前玩家从位置$s$获胜的概率。 该神经网络将策略网络和价值网络的角色组合到一个架构中。神经网络替换成了ResNet的结构。

在每一个位置$s$，在神经网络$f_{\theta }$的引导下执行MCTS搜索。MCTS搜索输出每一步的概率$\pi$。 这些搜索概率通常会选择比神经网络$f_{\theta }(s)$的原始行为概率$\mathbf{p}$更优的行为； 因此，MCTS可以被视为强大的策略改进方法。 在self-play过程中使用搜索，使用improved MCTS-based policy来选择每一步动作，使用游戏赢家$z$更新value，这同时也可以被视为强大的策略评估改进方法。

在策略迭代过程中重复使用这些搜索方法：神经网络的参数被更新，以使移动概率和值$(\mathbf{p},v)=f_{\theta }(s)$与改进的搜索概率和selfplay游戏赢家$(\pi ,z)$更加匹配；这些新参数将在下一次selfplay的迭代中使用，以使搜索更加强大。 图1展示了自学训练pipline。

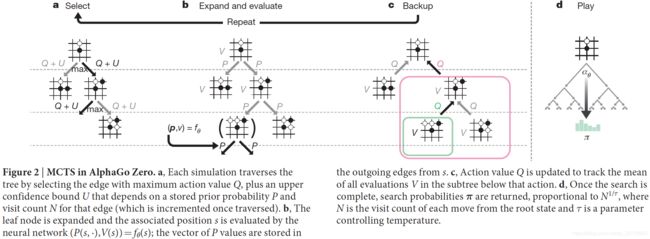
如图2所示，MCTS使用神经网络$f_{\theta }$引导搜索，反过来搜索结果用于更新网络。每一个边$(s,a)$包含先验概率$P(s,a)$，访问次数$N(s,a)$，行为价值$Q(s,a)$。每次模拟都是从根节点开始，迭代地选择动作以最大化下式：

直到叶子节点$s^{\prime }$不包含在树内。此叶子节点仅展开与评估一次，使用网络预测其先验概率与评估值，$(P(s^{\prime },\cdot ),V(s^{\prime }))=f_{\theta }(s^{\prime })$。然后所有遍历到的边$(s,a)$都需要增量更新访问次数和行为价值。

这一基于MCTS的强化学习算法可以看做以网络参数$\theta$和根位置$s$为输入，计算输出行为概率，$\pi ={\alpha }_{\theta }(s)$。与每一步访问次数的指数成正比，${\pi }_a\propto N(s,a{)}^{1/\tau }$，$\tau$为温度系数。

神经网络具体训练步骤如下：

• 初始化神经网络权重为${\theta }_0$；
• 在每个后续迭代$i\ge 1$时，都会产生self-play的游戏（图1a）；
• 在每一时间步$t$，使用神经网络的先前迭代版本$f_{{\theta }_{i-1}}$执行MCTS搜索${\pi }_t={\alpha }_{i-1}(s_t)$，并通过对搜索概率${\pi }_t$进行采样来选择动作；
• 游戏在步骤$T$终止，其终止条件为：①两个玩家都放弃落子；②搜索值下降到辞阈值以下；③游戏超过最大长度；
• 对游戏进行计分，以得到$r_T\in \{-1，+1\}$的最终奖励；
• 每个时间步$t$的数据都存储为$(s_t,{\pi }_t,z_t)$，其中$z_t=\pm r_T$是从当前玩家的角度来看在步骤$t$的游戏获胜者。 并行地（图1b），新网络参数${\theta }_i$是根据selfplay的最后一次迭代的所有时间步中均匀采样的数据$(s,\pi ,z)$训练的；
• 更新网络$(\mathbf{p},v)=f_{\theta }(s)$，网络损失由MSE、交叉熵损失和正则化构成：
  

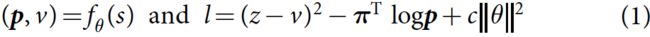
Empirical analysis of AlphaGo Zero training

从完全随机行为开始训练，结果如图3所示。在整个训练过程中，学习进展顺利，并且没有遭受先前文献中提到的振荡或灾难性遗忘。AlphaGo Zero训练36小时后就超越了AlphaGo Lee，72小时后超越了最新版本的AlphaGo Lee（打败李世石的版本），而AlphaGo Lee训练了几个月。此外，AlphaGo Zero仅使用a single machine with 4 tensor processing units (TPUs)，而AlphaGo Lee使用了many machines and used 48 TPUs。

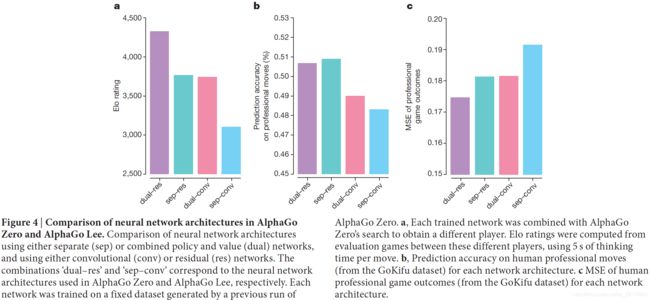
图4验证了AlphaGo Zero中网络结构和算法（单一网络）的贡献。使用AlphaGo Lee中独立的策略和价值网络，或AlphaGo Zero中的组合策略和价值网络，创建了四个神经网络；并使用AlphaGo Lee的卷积网络架构或AlphaGo Zero的残差网络架构。在72小时的self-play训练后，使用由AlphaGo Zero生成的固定的自玩游戏数据集，对每个网络进行了训练，以最大程度地减少相同的损失函数（等式（1））。实验表明使用残差网络更加准确，在AlphaGo中实现了600 Elo的降低，误差更低，并且性能得到了改善。将策略和价值组合到一个网络中会稍微降低移动预测的准确性，但会减少价值错误，并使AlphaGo的游戏性能再提高600 Elo。这部分是由于提高了计算效率，但更重要的是，双重目标将网络调整为支持多个用例的通用表示形式。

METHODS

Reinforcement learning.

主要包括策略迭代过程（即策略评估与策略改进）。AlphaGo Zero selfplay算法可以理解为一种近似的策略迭代方案，其中MCTS用于策略改进和策略评估。 策略改进始于神经网络策略，根据该策略的建议执行MCTS，然后将（更强大的）搜索策略投影回神经网络的功能空间。 策略评估应用于（更强大的）搜索策略：selfplay的结果也被投射回神经网络的功能空间。 这些投影步骤是通过训练神经网络参数以分别匹配搜索概率和selfplay结果来实现的。

Self-play reinforcement learning in games.

zero-sum，perfect information。

MCTS可以被视为selfplay强化学习的一种形式。搜索树的节点包含搜索过程中遇到位置的值函数，这些值被更新以预测自玩模拟游戏的获胜者。

Domain knowledge.

• 完美的围棋规则知识。用于在MCTS中得到执行某一动作后的下一状态，以及判断终止状态；
• 在MCTS模拟和自我训练中使用Tromp–Taylor评分。 这是因为如果游戏在解决边界之前终止，则人类分数（中文，日文或韩文规则）的定义不明确；
• 将描述位置的输入特征构造为19×19的图像，即神经网络结构与棋盘的网格结构相匹配；
• Go的规则在旋转和反射下是不变的，对于颜色转置也是不变的。

AlphaGo Zero从神经网络的随机初始参数开始。神经网络架构基于图像识别的最新技术，并相应地选择了用于训练的超参数。 MCTS搜索参数是通过高斯过程优化选择的，以便使用在初步运行中训练的神经网络来优化AlphaGo Zero的selfplay性能。 对于较大的运行（40个块，40天），使用在较小的运行（20个块，3天）中训练的神经网络对MCTS搜索参数进行了重新优化。

Self-play training pipeline.

AlphaGo Zero的self-play training pipeline由三个主要组件组成，所有这些组件都是并行异步执行的。

• 神经网络参数${\theta }_i$从最近的selfplay数据不断优化；
• 持续评估AlphaGo Zero玩家${\alpha }_{{\theta }_i}$；
• 到目前为止，表现最佳的播放器${\alpha }_{{\theta }_{\ast }}$用于生成新的selfplay数据。

Optimization.

每个神经网络$f_{{\theta }_i}$批量大小是每个woker32个，最小批量大小为2,048。 从最近的500,000场selfplay的所有位置中随机地对每个mini-batch数据进行统一采样。 使用等式（1）中的损失，通过具有动量和学习速率退火的随机梯度下降来优化神经网络参数。 根据扩展数据表3中的标准时间表对学习率进行退火。动量参数设置为0.9。 交叉熵和MSE损失的权重相等（这是合理的，因为奖励是按比例缩放的，$r\in \{-1，+1\}$），L2正则化参数设置为c = 10-4。 优化过程每1,000个训练步骤产生一个新的检查点。 这个检查点由评估者评估，并且可以用于生成下一批selfplay。

Evaluator.

为确保始终生成最佳质量的数据，我们在将其用于数据生成之前，针对当前最佳网络$f_{{\theta }_{\ast }}$评估每个新的神经网络检查点。 通过MCTS搜索${\alpha }_{{\theta }_i}$的性能来评估神经网络$f_{{\theta }_i}$，MCTS搜索${\alpha }_{{\theta }_i}$使用$f_{{\theta }_i}$来评估叶子位置和先验概率（请参阅搜索算法）。 每次评估包括400场比赛，使用具有1600次模拟的MCTS通过无限的温度$\tau \to 0$（即，我们确定地选择访问次数最多的棋局，以尽可能发挥最大的优势）来选择棋局。 如果新玩家以大于55％的赢率获胜（避免单独选择噪音），则它将成为最佳玩家${\alpha }_{{\theta }_{\ast }}$，并随后用于selfplay的产生，并成为后续比较的基准。

Self-play.

由evaluator选择的最佳当前player ${\alpha }_{{\theta }_{\ast }}$用于生成数据。 在每次迭代中，${\alpha }_{{\theta }_{\ast }}$进行25,000场selfplay，使用1,600个MCTS模拟选择每个动作（每次搜索大约需要0.4 s）。 对于每个游戏的前30个动作，温度设置为$\tau =1$； 这样可以根据他们在MCTS中的访问次数按比例选择动作，并确保遇到各种各样的位置。 在游戏的其余部分，将使用无穷小的温度，$\tau =0$。通过在根节点$s_0$中的先验概率上加上Dirichlet噪声，$P(s,a)=(1-\epsilon )p_a+\epsilon {\eta }_a$，其中$\eta 〜Dir(0.03)$，$\epsilon =0.25$，可以进行进一步的探索。 这种噪音确保可以尝试所有动作，但是搜索仍可能否决不良动作。为了节省计算量，显然输了的游戏都被放弃了。放弃阈值$v_{resign}$被自动选择，以将误报率（如果AlphaGo没有放弃，本可以获胜的游戏）保持在5%以下。为了衡量误报，我们在10%的self-play游戏中禁用放弃，并一直玩到终止。

Search algorithm.

搜索树中的每个节点$s$都包含所有合法动作$a\in A(s)$的边$(s,a)$。每个边存储一组统计信息：

其中$N(s,a)$是访问次数，$W(s,a)$是总动作值，$Q(s,a)$是平均动作值，$P(s，a)$是选择该边的先验概率 。 在单独的搜索线程上并行执行多个模拟。 该算法通过在三个阶段上迭代进行（图2a–c），然后选择要进行的移动（图2d）。

Select (Fig. 2a).

选择阶段几乎与AlphaGo相同。 这里简要介绍一下完整性。 每个模拟的第一个树内阶段从搜索树的根节点$s_0$开始，当模拟到达在时间步长$L$的叶节点$s_L$时结束。在每个时间步长$t<L$， 使用PUCT算法的一种变体，根据搜索树中的统计信息，$a_t=\underset{a}{\mathrm{argmax}}(Q(s_t,a)+U(s_t,a))$处选择动作：

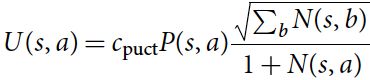
$c_{puct}$是确定勘探水平的常数； 此搜索控制策略最初会选择具有较高先验概率和较低访问量的动作，但渐近地会选择具有较高动作价值的动作。

Expand and evaluate (Fig. 2b).

将叶子节点$s_L$添加到队列中以进行神经网络评估，$(d_i(p),v）=f_{\theta }(d_i(s_L))$，其中$d_i$是从$[1..8]$中的$i$随机选择的二面镜像或旋转。 8]。 队列中的位置由神经网络使用最小批处理大小8来评估； 搜索线程将被锁定，直到评估完成。 叶节点被展开，每个边$(s_L,a)$初始化为$\{N(s_L,a)=0,W(s_L,a)=0,Q(s_L,a)=0,P(s_L,a)=p_a\}$; 然后backup值$v$。

Backup (Fig. 2c).

在每个步骤$t\le L$的反向传递中更新边的统计信息。访问计数递增$N(s_t,a_t)=N(s_t,a_t)+1$，并且将动作值更新为平均值，$W(s_t,a_t)=W(s_t,a_t)+v,Q(s_t,a_t)=\frac{W(s_t,a_t)}{N(s_t,a_t)}$。 我们使用virtual loss确保每个线程计算不同的节点。

Play (Fig. 2d).

搜索结束时，AlphaGo Zero选择一个根位置$s_0$的移动$a$，该移动$a$与它的访问计数的指数成正比，$\pi (a|s_0)=N(s_0,a{)}^{1/\tau }/{\Sigma }_{b}N(s_0,b{)}^{1/\tau }$，其中$\tau$是控制勘探水平的温度参数。 搜索树将在随后的时间步中重用：所选动作对应的子节点成为新的根节点； 该子树下的子树及其所有统计信息都将保留，而树的其余部分将被丢弃。 如果其根价值和最佳子价值低于阈值$v_{resign}$，则AlphaGo Zero将退出。

与AlphaGo Fan和AlphaGo Lee中的MCTS相比，主要区别在于AlphaGo Zero不使用任何rollouts。 它使用单个神经网络而不是单独的策略和价值网络； 叶节点始终被扩展，而不是使用动态扩展； 每个搜索线程仅等待神经网络评估，而不是异步执行评估和备份。 而且没有树政策。 在大型（40个blocks，40天）的AlphaGo Zero实例中也使用了transposition table。

Neural network architecture.

神经网络的输入是一个19×19×17图像堆栈，其中包含17个二进制特征平面。 八个特征平面$X_t$由指示当前玩家的棋子是否存在的二进制值组成（如果交叉点$i$在时间步长$t$时包含玩家颜色的石头，则$X_i^t=1$；如果交叉点为空，包含对手棋子，或者$t<0$，则为0）。 另外8个特征平面$Y_t$代表对手棋子的相应特征。 最后一个特征平面C代表所play的颜色，并且如果执黑子则常量值为1，如果执白子，则常量值为0。 这些平面串联在一起以提供输入特征$s_t=[X_t，Y_t，X_{t-1}，Y_{t-1}，...，X_{t-7}，Y_{t-7}，C]$。 历史特征$X_t$，$Y_t$是必需的，因为Go不能完全从当前的棋子上观察到，因为禁止重复。 类似地，颜色特征C是必需的，因为无法观察到komi。

输入特征$s_t$由residual tower处理，residual tower由单个卷积块和19个或39个残差块组成。卷积block应用了以下模块：

residual tower的输出传递到两个单独的“头”中，以计算策略和价值。 策略head应用以下模块：

对应于所有交叉点和pass的logit概率。

价值head应用以下模块：

在20或40块网络中，残差塔的总网络深度分别为39或79个参数化层，加上策略头的额外2层和价值头的3层。