算法特别篇_并查集思路(LeetCode_778_水位上升的泳池中游泳)
算法特别篇_并查集思路
概:近一个月leetcode出了一个月的并查集每日一题,有人惊呼:“这个月不学会并查集谁也别想走”,于是在通过找一些资料学习,并锤炼一些每日一题后,我有了自己的感悟,决定记下来。本篇主要讲述并查集抽象思维和案例(LeetCode_778_水位上升的泳池中游泳)的做法。
来源:力扣(LeetCode)
链接:LeetCode_778_水位上升的泳池中游泳
并查集抽象思路
- 声明:由于我在算法方面也是个菜鸡的缘故,遂一下内容可能会有不妥之处,还望大佬指正。
- 并查集有什么用:你可以看成一张图,图中有很多个节点,然后你需要让某俩个节点可以“连通”(即一个点可以通过其他若干个点到达另一个点)起来,这时候可能就用的到并查集了。再或者说,有一堆数据,你需要为其归类,存在某种联系的数据归为一类,这种联系题中给你了,你需要把一对有这种联系的数据归到一起,a与b一类,b与c一类,并查集会把a和c自动归到一起,所以你只需要向前看,把题中给好的直接俩俩关系凑到一起,不需要管间接关系的问题(这一手叫做没有后顾之忧)。
- 并查集怎么用:
- 并查集的形象上来说其实类似树结构,a节点和b节点要相连,就把a作为b的父节点或者b作为a的父节点。
- 假设有这么一种情况,b为a的父节点,d为c的父节点,如下图:
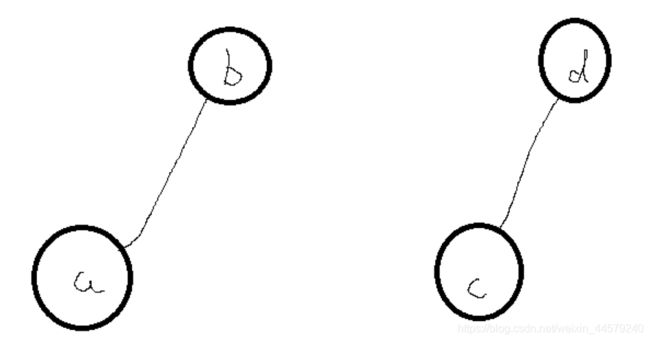
这时候题中的条件给你说a和c是要连上的,如果你把a和c直接相连,会形成这种情况:
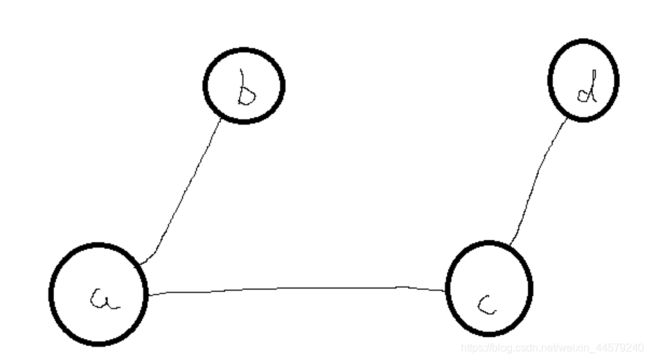
a的根节点是b,c的根节点是d,之后读取这个结构怎么判断a和c是否连接上了呢,(如果你很老实的给每个节点很大一块空间,存了其所有的连接节点,那就是正常的构图了,不属于并查集范畴),所以如果这时候我们是让a的父节点归于c的父节点之下,即b成为d的子节点如下图:
这时候就可以通过同一个根节点来判断,a和c是连通的。
- 并查集类实现的核心:
- 有一个parents集合,来表示点与点之间的关系,可以是数组,parents[i]表示数据i的父节点的值。也可以是map直接映射俩个点的数据。
- 构造方法,主要任务是实现空间的开拓和初始化,如果你用map动态来的话当我没说,如果是数组,那么每个点最开始都要设置好默认的值,默认没有父节点,那么父节点设置为自己本身,检索的时候就会检查到当前点为根节点。
- Find方法,用来查询某个值的根节点是谁,如果parents[i]==i,那么说明当前节点自身就是根节点了(其没有父节点),否则其根节点就是其父节点的根节点,也就是Find(parents[i]);
- marge方法,我叫其为合并,主要用来实现将俩个有联系的节点连接到一起,当然,说的不是直接连起来,而是归为同一跟下,就是上面图说的将某一节点的根归到另一个节点的根下面。所以这个方法首先判断其是否为同一根下,如果是,则结束,如果不是,则让其中一个点的根归到另一个节点的根下。
- 大概要实现的核心如上,根据题目的要求,在做一些简单逻辑上的修改,拿到自己需要的数据即可。
- 做并查集需要抽象出的信息:
- 节点本身是什么
- 节点间的关系是什么
- 如何遍历节点间的关系,让其连接起来
- 最后需要得到的数据是什么
题目
在一个 N x N 的坐标方格 grid 中,每一个方格的值 grid[i][j] 表示在位置 (i,j) 的平台高度。
现在开始下雨了。当时间为 t 时,此时雨水导致水池中任意位置的水位为 t 。你可以从一个平台游向四周相邻的任意一个平台,但是前提是此时水位必须同时淹没这两个平台。假定你可以瞬间移动无限距离,也就是默认在方格内部游动是不耗时的。当然,在你游泳的时候你必须待在坐标方格里面。
你从坐标方格的左上平台 (0,0) 出发。最少耗时多久你才能到达坐标方格的右下平台 (N-1, N-1)?
示例
示例 1:
输入: [[0,2],[1,3]]
输出: 3
解释:
时间为0时,你位于坐标方格的位置为 (0, 0)。
此时你不能游向任意方向,因为四个相邻方向平台的高度都大于当前时间为 0 时的水位。
等时间到达 3 时,你才可以游向平台 (1, 1). 因为此时的水位是 3,坐标方格中的平台没有比水位 3 更高的,所以你可以游向坐标方格中的任意位置
示例2:
输入: [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]]
输出: 16
解释:
0 1 2 3 4
24 23 22 21 5
12 13 14 15 16
11 17 18 19 20
10 9 8 7 6
最终的路线用加粗进行了标记。
我们必须等到时间为 16,此时才能保证平台 (0, 0) 和 (4, 4) 是连通的
提示
1)2 <= N <= 50.
2)grid[i][j] 是 [0, …, N*N - 1] 的排列。
思路
- 首先读完题知道题目要做什么:水位达到某一高度后,你可以从左上角点位游到最下角点位,求这个最低高度。
- 然后去抽象并查集四大信息:1. 节点本身就是它的坐标(x,y),而通过提示我们可以知道,x和y不会超过50,那么我们可以将x和y压缩到一个int数据中,既有:x*每行个数+y。得到的int数据是唯一且连续的,我们可以用其作为节点本身的参照。2. 节点间的关系是四面相邻,从一个点出发,只能直接到达其相邻点位,并且当水位高过当前点位的时候,你才能从当前点位出发,然后游到相邻的四个点位中比当前水位低的点。3. 如何遍历,由于题目中说了是要求最低水位,所以我们以水位上升作为变量来一步步去连接节点。当水位升到某一高度后,等于该高度的平台就可以和四周更低高度的平台相连,调用marge方法。4. 要得到的值是允许左上角点与右下角点连通的最低水位值,所以当某一次水位上升合并完平台之后,我们检查当前左上角与右下角点位是否连通,若连通直接返回当前水位即可。
c++完整代码
class Unionfind
{
public:
vector<int> parents;
Unionfind(int n)
{
for (int i = 0; i < n; i++)
{
parents.push_back(i);
}
}
int Find(int x)
{
if (parents[x] == x) return x;
else return Find(parents[x]);
}
void marge(int x,int y)
{
if (Find(x) != Find(y))
{
parents[Find(x)] = Find(y);
}
}
bool rt()
{
if (Find(0) == Find(parents.size() - 1)) return true;
else return false;
}
};
class Solution {
public:
map<int, vector<int>> ma;
int swimInWater(vector<vector<int>>& heights) {
for (int i = 0; i < heights.size(); i++)
for (int j = 0; j < heights[0].size(); j++)
{
insert(i* heights[0].size() + j, heights[i][j]);
}
Unionfind uf(heights.size() * heights[0].size());
map<int, vector<int>>::iterator it = ma.begin();
for (int i = 0; i < ma.size(); i++)
{
vector<int>& ve = it->second;
for (int j = 0; j < ve.size(); j ++)
{
int x = ve[j]/heights[0].size();
int y = ve[j]%heights[0].size();
if(x-1>=0&&heights[x-1][y]<=heights[x][y])
uf.marge(ve[j],ve[j]-heights[0].size());
if(x+1<heights.size()&&heights[x+1][y]<=heights[x][y])
uf.marge(ve[j],ve[j]+heights[0].size());
if(y-1>=0&&heights[x][y-1]<=heights[x][y])
uf.marge(ve[j],ve[j]-1);
if(y+1<heights[0].size()&&heights[x][y+1]<=heights[x][y])
uf.marge(ve[j],ve[j]+1);
}
if (uf.rt()) return it->first;
it++;
}
return 0;
}
void insert(int x, int h)
{
if (ma.count(h) == 0) ma.insert(pair<int, vector<int>>(h, vector<int>()));
ma.find(h)->second.push_back(x);
}
};