基于Qiskit——《量子计算编程实战》读书笔记(三)
目录
第4章 使用量子门演化量子态
门
IBM QX通用门集
哈达玛门
泡利门(X, Y, Z)
相门(S)和π/8门(T)
多量子比特门
练习和问题
欢迎加入Qiskit交流群: 1064371332
第4章 使用量子门演化量子态
门
本章代码:https://github.com/PacktPublishing/Mastering-Quantum-Computing-with-IBM-QX/tree/master/Chapter04
此所谓“门”者,并非 door,而是 gate.一如量子比特是经典比特的量子版本,量子寄存器是经典寄存器的量子版本一样,量子门是经典逻辑门的量子版本。沿循我们在第三章的经典与量子间的类比思路,本章中也会以同样方式处理经典门和量子门。
在经典计算中,经典门在经典寄存器上运行以演化(Evolve)其状态,在量子计算中,量子门在量子寄存器上运行以演化量子状态。
对于 经典逻辑门,百度百科给出如下信息:
MC玩家可能对此更为熟悉,在游戏社区中被广泛应用于所谓的“红石电路”,将红石的亮与灭对应于1和0:
【MC-红石】06 【不可能学不会】萌新红石入门首选必修课(七大逻辑门)
前文已经说过,每一个量子态都可以有一个矢量去对应,更何况我们既已定义![]() .故而很自然地可以想到,既然我们有向量来对应单量子态,那么象征着“变换”或“演化”的量子门,就可以对应于矩阵。但是,和第三章的推导一样,我们选取的数学工具必须保证变换结果也是一个量子态,意味着分量平方和仍应是1。为了进一步推导,我们需要联系Bloch球面,既然量子态都可以被描述成端点位于球面上的矢量,那么量子态间的变换也就可以被描述成幺正矩阵。在群论中,该类矩阵被归为SU(3),其中S意味着变换前后,矢量模长不会改变,数学上表现为其行列式为1。
.故而很自然地可以想到,既然我们有向量来对应单量子态,那么象征着“变换”或“演化”的量子门,就可以对应于矩阵。但是,和第三章的推导一样,我们选取的数学工具必须保证变换结果也是一个量子态,意味着分量平方和仍应是1。为了进一步推导,我们需要联系Bloch球面,既然量子态都可以被描述成端点位于球面上的矢量,那么量子态间的变换也就可以被描述成幺正矩阵。在群论中,该类矩阵被归为SU(3),其中S意味着变换前后,矢量模长不会改变,数学上表现为其行列式为1。
拓展知识:SU(2),SO(3)群笔记 - luyi07 - 博客园 (cnblogs.com)
在二维平面中,很典型的例子是旋转矩阵:
例如对零态:
这种变换令人大为满意!所以我们大可以说,旋转群对于不同的角度可以代表一系列量子门。
正式介绍全部量子门前,我们还需要注意几点(其实都是线性代数中的规定):
- 一系列门的作用顺序不能轻易改变,即交换律不一定成立,但是结合律却可以成立(联系矩阵的变换意义,尝试举出交换律不成立的例子);
- 左矢是右矢的转置加共轭,故而在左边作用于右矢的量子门绝对不能在左边作用左矢,也就是说
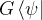 没有意义!
没有意义!
另,需知,上例中的量子门为单量子门,量子门之间也可以通过直积进行组合成为多量子门,当然相应作用的量子态也必须是多量子态。
IBM QX通用门集
接下来的介绍会十分单调乏味,希望读者诸君可以一边浏览代码定义,一边将其作用于不同量子态上,并用我们在第二章实现的绘图工具做出相应的布洛赫球面。
哈达玛门
几何意义:将初始量子比特绕x轴旋转180°,然后绕y轴旋转90°;
代码实现:
H=1./np.sqrt(2)*np.matrix('1 1;1 -1')泡利门(X, Y, Z)
数学定义:
几何意义:
- X门:将量子态绕X轴旋转180°;
- Y门:将量子态绕Y轴旋转180°;
- Z门:将量子态绕Z轴旋转180°;
代码实现:
X=np.matrix('0 1; 1 0')
Y=np.matrix([[0, -1j],[1j, 0]])
Z=np.matrix([[1,0],[0,-1]])相门(S)和π/8门(T)
几何意义:
- S门:将量子态绕z轴旋转90°;
- T门:将量子态绕z轴旋转45°(至于为什么是π/4弧度而不是π/8弧度,这和历史原因有关);
代码实现:
S=np.matrix([[1,0],[0,np.e**(j*np.pi/2.)]])
T=np.matrix([[1,0],[0, np.e**(j*np.pi/4.)]])其dagger门或称匕首门,亦即其共轭加转置:
S_dagger = S.conjugate().transpose()
T_dagger = T.conjugate().transpose()相应的几何意义和原先量子门大体一致:旋转角度相同,只是方向不一样。
运行以下代码,体会各量子门几何意义:
plot_bloch(H*zero_qubit)
plot_bloch(H*one_qubit)
plot_bloch(X*zero_qubit)
plot_bloch(X*one_qubit)
plot_bloch(Y*zero_qubit)
plot_bloch(Y*one_qubit)
plot_bloch(Z*zero_qubit)
plot_bloch(Z*one_qubit)
plot_bloch(zero_qubit)
plot_bloch(S*zero_qubit)
plot_bloch(T*zero_qubit)
plot_bloch(T*T*zero_qubit)多量子比特门
本节重点介绍一种极其重要的多量子比特门:CNOT,其重要性就在于其能生成纠缠态。
| 起始状态 | CNOT 门操作后状态 |
|---|---|
| | 00 > | | 00 > |
| | 01 > | | 01 > |
| | 10 > | | 11 > |
| | 11 > | | 10 > |
稍加观察与思考,不难发现,第二个比特位的量子态变化与否实际上取决于第一个量子态是1还是0.所以,我们叫第一个量子比特为控制位(control, 但实质上是作用的条件),第二个量子比特为目标位(target,但实质上是作用的结果)。
那么好,现在让我们考虑一个正零双量子态:
![]()
现在将CNOT门作用于其上:
![]()
思考:为什么得到这样一个结果?
数学定义:
代码实现:
CNOT=np.matrix('1 0 0 0; 0 1 0 0; 0 0 0 1; 0 0 1 0')由于我们目前处理的是双量子态,继续用布洛赫球绘图不免有些不合适,故而需要一个新函数来检验我们的算法:
def measure_in_01_basis(state):
from random import random
n_qubits=int(log(state.shape[0],2))
probabilities=[(coeff*coeff.conjugate()).real for coeff in state.flat]
rand=random()
for idx,state_desc in enumerate([''.join(map(str,state_desc))
for state_desc in itertools.product([0, 1], repeat=n_qubits)]):
if rand < sum(probabilities[0:(idx+1)]):
return '|"%s">' % state_desc
def probability_table_in_01_basis(state,n_measurements=1000):
from collections import Counter
measured=[measure_in_01_basis(final_state) for i in range(n_measurements)]
for s,c in Counter(measured).items():
print(s,"{0:.0%}".format(c/n_measurements))
starting_state=create_quantum_state([plus_qubit,zero_qubit])
final_state=CNOT*starting_state
probability_table_in_01_basis(final_state)注意,代码逻辑中有一处是违背量子计算原则的,即重复测量了同一个量子态并假定它不会坍缩到某一经典状态。在实际操作中,我们需要提前制备大量相同量子态,并对其中每一个态进行逐个测量,最后得到结果。
原书上附加了额外的一个例子,即以第一个量子比特为目标位,第二个量子比特为控制位:
CNOT_control1_target0=np.kron(H,H)*CNOT*np.kron(H,H) 除了思考这个例子,我还希望你能思考一下,对于n元多量子态,怎样才能任意指定控制位和目标位呢? 进一步,相应量子门的矩阵如何写出?(提示,运用行或列对调的思想)
练习和问题


![\\Rot(\theta)=\left[\begin{matrix} cos(\theta)&sin(\theta)\\-sin(\theta)&cos(\theta)\end{matrix} \right ]\\ det(Rot(\theta))=cos^2(\theta)-(-sin(\theta))(sin(\theta))=1](http://img.e-com-net.com/image/info8/3815573470924f9d87b1e01a9cc151f4.png)

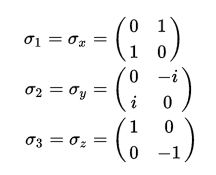
![CNOT=\left[ \begin{matrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&0&1\\ 0&0&1&0 \end{matrix} \right]](http://img.e-com-net.com/image/info8/80d12c8f7f4042c09a358e147127743b.png)