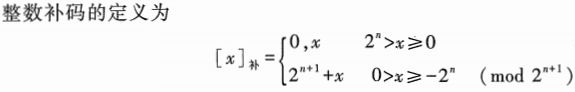计算机的运算方法
无符号数
定义:没有符号的数,在寄存器中的每一位均可用来存放数值
表示范围:n 位无符号数 0~2n -1
有符号数
定义:符号位+数值位
“0”代表正,“1”代表负
表示范围:n 位有符号整数
原码、反码: -(2n-1 -1)~ 2n-1 -1【关于原点对称】 ,一共 2n -1 个数
补码:-2n-1 ~ 2n-1 -1,一共 2n 个数
原码
地位:原码是机器数中最简单的一种表示形式,符号位为 0 表示正数,为 1 表示负数,数值位即真值的绝对值
原码表示:带符号的绝对值表示
书写要求:整数的符号位与数值位之间用逗号隔开
小数的符号位与数值位之间用小数点隔开
真值零的原码表示有正零和负零两种形式,[+0]原 =00000 和 [-0]原 =10000
反码
正数:反码和原码表示相同
负数:符号位为1,数值位按位取反(即符号位不变,数值位按位取反)
真值零的反码表示不唯一,负数的反码符号位为“1”,数值部分取反,[+0]反 =0.0000,[-0]反 =1.1111
补码
一个负数可用其正补数代替,该正补数用模加负数本身求得
一个正数和一个负数互为补数时,绝对值之和为模数
正数的补数即该正数
正数:补码和原码表示相同
负数:反码+1
真值零的补码表示是唯一的,[+0]补 =[-0]补 =0.0000
移码
移码:在真值 X 上加上一个常数(偏置值),通常该常数取 2n ,n+1 位有符号数
同一真值的补码和移码仅差一个符号位,将补码的符号位由“0”改为“1”,或从“1”改为“0”,即可得该真值的移码
数的表示
定点表示
定点数:小数点固定在某一位置的数(约定小数点位置不变)
浮点表示
小数点的位置可用浮动
表示形式
表示范围
浮点数的规格化
目的
提高浮点数的精确度
左规
算数左移,阶码-1
右规
算数右移,阶码+1
规格化操作
基数为 2,尾数的最高位为1的数为规格化数;规格化时,尾数左移一位,阶码-1,尾数右移一位,阶码+1
基数为4,尾数的最高两位不全为0的数为规格化数;规格化时,尾数左移两位,阶码-1,尾数右移两位,阶码+1
基数为8,尾数的最高三位不全为0的数为规格化数;规格化时,尾数左移三位,阶码-1,尾数右移三位,阶码+1
发电机中一旦基数确定就不再改变,基数是隐含的,不同基数的浮点数表示形式完全不同
基数不同,对数的表示范围和精度等都有影响
基数 r 越大,可表示的浮点数范围越大,所表示的数的个数越多,浮点数的精度下降
IEEE 754 标准
阶码部分含阶符
数符:表示浮点数的正负,与其有效位(尾数)是分开的
- 对于规格化的二进制浮点数,数值的最高位总是“1”,为了能使尾数多表示一位有效位,将这个“1”隐含,因此尾数数值实际上是24位。隐含的“1”是一位整数。
移位运算
意义:二进制表示的机器数在相对于小数点作 n 位左移或右移时,其实质就是该数乘以或除以2n
逻辑移位
移位对象:无符号数
操作:逻辑左移时,高位移丢,低位补0;逻辑右移,地位移丢,高位补0
算术移位
移位对象:有符号数
操作:符号位保持不变,仅对数值位进行移位
正数
原码=反码=补码=真值,移位后出现的空位均补0
负数
原码
移位后出现的空位补0
反码
移位后出现的空位补1
补码
负数的补码=反码+1,导致反码最右边几个连续的1因进位变为0,直到进位碰到第一个0为止,所以,负数补码中,最右边的1及其右边同原码,左边同反码
左移后出现的空位补0,右移后出现的空位补1
加法与减法运算
加减法运算是计算机中最基本的运算
减法运算可看作被减数加上一个减数的负值,即 A-B=A+(-B)
补码加减法运算
补码表示的两个数进行加法运算时,可把符号位与数值位同等处理,只要结果不超出机器能表示的数值范围,运算后的结果按 2n+1 取模(对于整数)或按 2 取模(对于小数),可得到本次加法的运算结果
取模的意义:丢掉最左边的进位
基本思路
[-B]补 由 [B]补 连同符号位在内,每位取反+1得到
溢出判断
一位符号位判断溢出
对于加法,只有正数+正数和负数+负数两种情况下才可能出现溢出,符号不同的两个数相加,是不会溢出
正数+正数=负数,上溢
负数+负数=正数,下溢
对于减法,只有正数-负数或负数-正数两种情况下才可能出现溢出,符号相同的两个数相减,是不会溢出的
两位符号位判断溢出
2 位符号位不同时,表示溢出,否则,无溢出
乘法运算
原码乘法
原码一位乘运算规则
原码一位乘所需的硬件配置
A、X、Q 为 n+1 位寄存器
X:存放被乘数的原码
Q:存放乘数的原码
末尾乘数 Qn :控制移位和加控制电路( 当 Qn = 1 时,A 和 X 内容相加后,A、Q 右移一位;当 Qn =0 时,只作 A、Q 右移一位操作 )
C:控制逐位相乘的次数
S:存放乘积的符号
GM :乘法标记
原码一位乘控制流程
原码两位乘
原码两位乘,与原码一位乘一样,符号位和数值位的运算分开进行
用两位乘数的状态决定新的部分积如何形成,提高运算速度
除法运算
笔算除法
原码除法
实际上用补码进行运算
恢复余数法
特点:当余数为负时,需加上除数,将其恢复成原来的余数
商值的确定通过比较被除数和除数的绝对值大小 x*-y* 实现,因计算机内只设加法器,故将 x*-y* 变为[x*]补+[-y*]补 操作
不恢复余数法
浮点运算
浮点加减
当两浮点数阶码不等时,两尾数小数点的实际位置不一样,位数部分无法直接进行加减运算
运算步骤
- 对阶
- 尾数求和
- 规格化
- 舍入
- 溢出判断
对阶
目的:使两数的小数点位置对齐,即使两数的阶码相等
原则:小阶向大阶看齐,使阶小的尾数向右移动,右移的次数等于阶差
尾数右移可能会发生数码丢失,影响精度
尾数求和
操作:将对阶后的两尾数按定点加减运算规则求和(差)
规格化
目的:增加有效数字的位数,提高运算精度,必须将求和(差)后的尾数规格化
左规:00.0XX...X 或 11.1XX...X
右规:01.XX...X 或 10.XX...X
舍入
目的:提高精度,要考虑尾数右移时丢失的数值位
“0 舍 1 入”法:尾数右移时,被移去的最高数值位为 0,舍去;被移去的最高数值位为 1,则在尾数的末位+1。这样做可能使得尾数溢出,需再做一次右规
“恒置 1”法:尾数右移时,不论丢掉的最高数值位是“1”或“0”,都使右移后的尾数末尾恒置“1”
溢出判断
尾数出现 01.XXX 或 10.XXX 不表示这一浮点数溢出,只有将此数右规后,才能再根据阶码判断浮点运算结果是否溢出