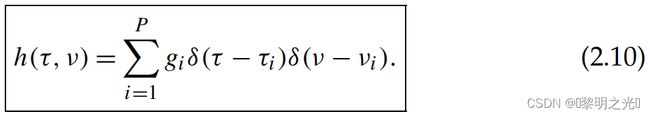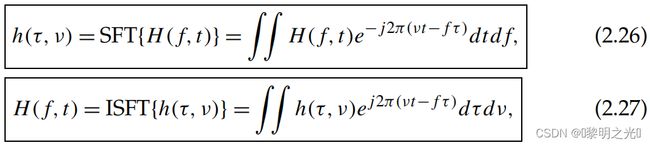High-mobility wireless channels 高速移动信道的信道特征
1. Introduction
任何传输的信号在通过无线信道传播时都会发生变化。有几个因素,包括信道传播延时,在传播路径中的障碍(引起接收信号强度的波动)通常称为衰落。衰落可以大致可分为大规模衰落和小尺度衰落。
大规模衰落涉及由于信号在长距离(超过几百米)传播而导致的平均接收信号强度的变化,以及由于传播路径中存在大障碍造成的阴影而造成的完全或部分视线(LoS)路径损失。
另一方面,小尺度衰落指的是在短时间内(秒量级)或短距离内(米量级)内发生的快速波动。这些波动是由于通过不同的传播路径到达的传输信号回波的构造和破坏性叠加而引起的,这种现象被称为多路径传播。
本章将重点讨论小规模衰落,因为通信系统的物理层设计是基于对抗无线信道的小规模衰落。由于我们关注的是延迟多普勒通信,因此在后面的章节中深入讨论收发器设计的更实际方面之前,深入了解信道的延迟多普勒域表示是至关重要的。时延多普勒域与反射器的距离和相对速度等环境的物理几何参数非常相似。在接收机附近有有限的反射器数量的实际假设下,与传统的延迟时间或频率时域相比,延迟-多普勒域提供了更紧凑的几何信道表示。
2. Input–output model of the wireless channel
考虑在无线信道上传输信号。在发射机处,带宽B的基带信号s (t)被上转换为通带[fc−B/2,fc + B/2],其中fc是用于传输的载波频率。在接收机,接收到的信号下转换为基带等效信号,用r (t)表示。由于大多数接收机处理,如解调、解码和检测,都发生在基带上,因此我们将只关注无线信道的基带等效表示。为了最终得到信道的延迟-多普勒表示,我们从一个无线信道的几何模型开始。
2.1 几何模型
几何模型是基于光线追踪技术(ray-tracing technique),这是理解传输波如何干扰一个实际的物理信道的一个简单和有用的工具。为了推导出无线信道的确定性模型,我们从光线追踪技术开始,并利用传播环境的物理几何知识。由于多路径传播,接收信号r (t)是传输信号s (t)的延迟、多普勒位移和衰减副本的集合。延迟是每个传播路径长度的函数,而多普勒频移是由于发射机、接收器和反射器场景中的相对运动而发生的。
让我们首先考虑图中所示的一个简单的无线信道,其中发射机(基站)、接收机(移动)和反射器(建筑物)都是静态的。由于在场景中没有相对运动,所以传输的信号不发生任何多普勒频移。然而,直接路径和反射路径的传播延迟的差异导致s (t)的两个副本在不同的时间到达移动接收机。由于距离r1,从基站到移动设备的直接路径会产生传播延迟。另一方面,从建筑反射的路径必须经过r2+r3的总距离。假设直接路径和重复弯曲路径分别具有g1和g2的基带等效复增益(衰减)。利用叠加原理,接收信号r (t)可以表示为
其中,τ1 = r1/c为LoS路径的延迟,τ2 =(r2 + r3)/c为反射路径的延迟,c = 3·10^8 m/s为光速。传播延迟的差异τ2−τ1被称为传播延迟(delay spread)。注:在两条以上路径的信道中,延迟扩展定义为最长和最短路径传播延迟的差,即τmax−τmin。
现在考虑一下图中的另外一种情况,其中移动接收机是在一辆以相对速度υ向基站移动的汽车中。
我们可以假设s (t)的带宽B与载波频率fc相比非常小,即fc>>B。由相对速度υ引起的多普勒频移由(υ /c)*fc给出。接收到的信号可以表示为传输信号的延迟和多普勒位移副本的和:
其中ν1 = (υ/c)*fc为LoS路径的多普勒频移,ν2 = (υ*cos θ/c)*fc为反射路径的多普勒频移,|ν2−ν1|为多普勒延迟(Doppler spread),随时间变化的函数可以被定义为:
表示由延迟和多普勒频移引起的传播路径的时变衰减。表2.1列出了一些典型无线信道的延迟扩散(τmax)和多普勒扩散(νmax)值。
一般来说,(2.3)中的多路径衰落信道可以被建模为一种形式的LTI系统
其中,g(τ,t)为信道的延迟-时间脉冲响应,0≤τ<∞表示传播延迟。通过沿着g(τ,t)的延迟维数进行傅里叶变换,可以得到信道在固定时间t下的时频脉冲响应H
在实践中,H(f,t)被认为是t的一个缓慢的时变函数。对于静态信道的特殊情况,即νi = 0,∀i,H(f,t)降低为与时间无关的频率响应H(f)。
2.2 信道的延迟多普勒表示
我们展示了不同的延迟和多普勒位移分量如何导致接收信号r (t)变化的,并定义了一个无线信道响应的模型。然而,多普勒频移的影响在我们在上一节中获得的延迟-时间响应g(τ,t)中并不明显。散射体的影响可以用发射信号的延迟(由于产生的距离)和多普勒频移(由于相对运动)来表示。这使得一个线性时间间隔的无线信道能够完全由接收机附近的散射体的深度多普勒参数来表征。由于延迟-多普勒响应更接近于物理无线信道,因此有一个信道的延迟-多普勒表示是有用的。一般来说,无线信道的小规模衰落效应可以用接收机附近的少量散射体来表示。这意味着无线信道在延迟-多普勒域中具有稀疏表示。为了明确地说明这一点,让我们考虑一个具有明显延迟和多普勒频移参数的P传播路径的无线信道。
公式(2.2)中给出的双路径输入输出关系可以推广为传播路径的数量为P个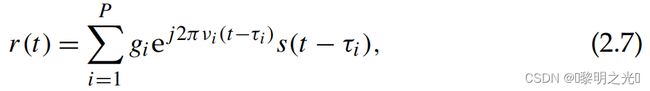 其中gi为路径增益,τi和νi分别为延迟和多普勒频移,即第=条路径,i = 1,...,P。我们将延迟-多普勒响应定义为
其中gi为路径增益,τi和νi分别为延迟和多普勒频移,即第=条路径,i = 1,...,P。我们将延迟-多普勒响应定义为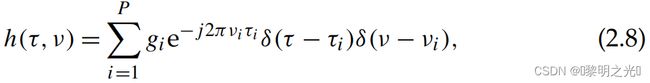 这是由于路径数量p的有限限制,无线信道在深度多普勒域内的稀疏表示,那么接收到的信号r (t)可以写为
这是由于路径数量p的有限限制,无线信道在深度多普勒域内的稀疏表示,那么接收到的信号r (t)可以写为
当传播路径有限时,无线信道在深度多普勒域内的稀疏表示,那么接收到的信号r (t)可以写为 从(2.8)中我们看到延迟多普勒领域的通道完全由参数(gi,τi,νi)其中i=1,...,p。注意e−j2πνiτi是一个恒定的相移,可能被吸收到通道系数gi符号轻微的滥用。在不丧失一般性的情况下,我们将简单地假设:
从(2.8)中我们看到延迟多普勒领域的通道完全由参数(gi,τi,νi)其中i=1,...,p。注意e−j2πνiτi是一个恒定的相移,可能被吸收到通道系数gi符号轻微的滥用。在不丧失一般性的情况下,我们将简单地假设:
下图中(a)和(b)显示了在高速公路上的基站(Tx)和车辆(Rx)之间的通道的简单延迟多普勒表示。这两张照片都是在时间间隔100 ms时拍摄的。请注意,传输的信号持续时间一般小于10 ms,这比几何相干时间要短得多,即信道的物理几何可以被认为是不变的持续时间。这使得信道只要脉冲在几何相干时间内传输那么延迟-多普勒域内的脉冲有一个大致的时不变响应。几何相干时间的知识对于根据延迟扩展和多普勒扩散等特定信道参数进行信号持续时间等传输参数的设计至关重要。
作为高移动性场景的一个例子,考虑图(a)和(b),显示了当场景的几何形状发生变化时,延迟-多普勒信道响应如何发生变化。
由于散射体的存在,Rx接收到传输信号的P延迟和多普勒频移回波的聚集。本例中考虑的散射体被标记为o1、o2和o3。图中的延迟多普勒网格显示了传输延迟和多普勒位置[0,0]时移动用户接收到的信息。延迟-多普勒网格中的每个彩色点对应于由相同的彩色射线表示的传播路径。延迟多普勒网格中点的面积表示每个传播路径的增益。假设沿延迟和多普勒轴的每个整数值对应于一个相对于Rx的距离为10 m且速度为50 km/h的反射器。例如,蓝色(打印版本中的黑色)点对应于相对于接收器Rx在50 km/h(对应于整数多普勒抽头=1)处移动的反射器。图(a)中最大的点对应于基站与接收车辆Rx之间的LoS路径,如蓝色所示。它被分配了一个延迟0,是第一个到达的信号,并有一个正的多普勒频移,因为汽车正在向基站移动。黄色(打印版中的浅灰色)圆圈对应的是在高速公路上沿着与Rx相同方向行驶的另一辆车辆(O1)反射的路径,但相对于基站,Rx的速度较低。最小的圆对应于最长的路径,这是由于(O2)的反射,用紫色(印刷版中的深灰色)点和光线表示。当车辆离开基站时,多普勒频移有一个负值,并且由于车辆之间的相对角度,此时其相对于Rx的相对速度为零。由于严重的路径衰减,车辆O3的反射被忽略,因为传输波的传播距离必须比o2的情况下长得多。
现在让我们讨论信道,以及延迟多普勒表示,如何在短时间内保持不变。如图(b)所示,在100 ms的空间内,车辆O2离Rx更远,O3离Rx更近。这导致O3的反射波(用红色(中灰色)点表示)比O2的反射波更强。由于o3以o2的速度运行,o3的多普勒频移小于o2的多普勒频移,几乎是o2的一半。从这个例子中得出的关键结论是,通过适当地设计帧持续时间,可以使典型无线信道的延迟-多普勒表示对信号帧的持续时间大致定不变。
2.4 不同通道表示形式之间的关系
从前章节中,当s (t)是传输的连续时域信号时,在时变多径信道(也称为双色散信道)下接收的信号r (t)可以写为
其中,S (f)是s (t)的傅里叶变换。(2.23)–(2.25)中的三个等价关系可以解释如下。(2.23)中的通道g(τ,t)表示时变脉冲响应,这种关系可以看作是LTI系统的直接推广。(2.24)中的关系描述了时频通道,并通过该关系定义了一个基于OFDM的系统。最后,(2.25)中的关系描述了延迟-多普勒信道,以及基于此关系的OTFS系统。时频域和时延多普勒域的图像关系为:
可以发现在时延多普勒域的表示下,多径信息能够显而易见。说明了与时频域信道相比在线性时变和时不变信道中的稀疏性。同时图中脉冲位置处的延迟-多普勒平面(τ,ν)表示具有相应的延迟和多普勒频移的路径的传播增益的幅度。在这种情况下,路径数被设置为P = 4。可以看出,第一幅中对应的频率-时间信道是时变的,因此需要更多的时频系数来准确地表示信道。而对于静态信道,频率-时间信道是时不变的,P路径如第二幅图所示。从时延表示可以看出,所有路径都有多普勒频移νi = 0,其中i=1,...,P。第二幅图代表一个频率选择通道,而第一幅图是时间和频率选择性,或者换句话说,双选择性。
现在,时频(H(f,t))和延迟多普勒(h(τ,ν))信道响应之间的关系可以由一对二维辛傅里叶变换(SFTs)给出:
其中(2.26)和(2.27)分别定义了SFT和ISFT操作,他们的具体关系如下:
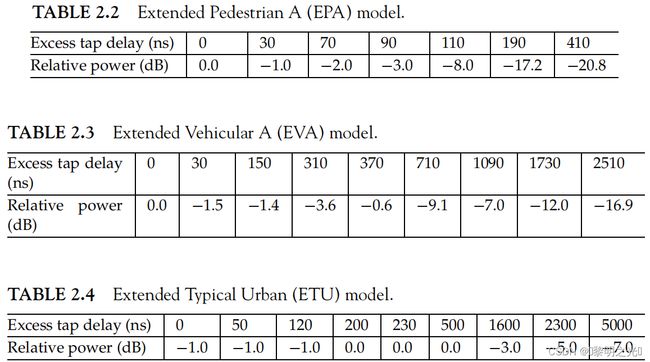
考虑到要进行信道建模和信道仿真,这里提供了多种不同的无线信道模型,我们列出了一些标准的3GPP多路径衰落信道配置文件,它们将用于生成信道模型,用于后面章节的模拟。这里列出的衰落模型代表了低、中和高延迟扩散环境。功率延迟曲线见表2.2、2.3、2.4。
设νmax = fcVmax/c为整个多径信道的最大多普勒频移。我们假设单个多普勒频移与第i个延迟路径相关联,并遵循经典的Jakes谱,即νi = νmax cos(θi),其中θi均匀分布在[−π,π]上。
Classover!本章结束^.^