AcWing算法基础课 Level-2 第三讲 搜索与图论

单链表

#include 
using namespace std;
const int N = 1e5 + 10;

// head 表示头结点的下标
// e[i] 表示节点i的值
// ne[i] 表示节点i的next指针是多少
// idx 存储当前已经用到了哪个点
int head, e[N], ne[N], idx;

// 初始化
void init()
{
    head = -1;
    idx = 0;
}

// 将x插到头结点
void add_to_head(int x)
{
    e[idx] = x, ne[idx] = head, head = idx ++ ;
}

// 将x插到下标是k的点后面
void add(int k, int x)
{
    e[idx] = x, ne[idx] = ne[k], ne[k] = idx ++ ;
}

// 将下标是k的点后面的点删掉
void remove(int k)
{
    ne[k] = ne[ne[k]];
}

int main()
{
    int m;
    cin >> m;

    init(); // 初始化

    while (m -- )
    {
        int k, x;
        char op;
        cin >> op;

        if (op == 'H')
        {
            cin >> x;
            add_to_head(x);
        }
        else if (op == 'D')
        {
            cin >> k;
            if (!k) head = ne[head];
            else remove(k - 1);
        }
        else{
            cin >> k >> x;
            add(k - 1, x);
        }
    }

    for (int i = head; i != -1; i = ne[i]) cout << e[i] << " ";
    cout << endl;
    return 0;
}

双链表

#include 
using namespace std;
const int N = 1e5 + 10;

int idx, l[N], r[N], e[N];

//在节点a的右边插入x
void insert(int a, int x)
{
    e[idx] = x;
    l[idx] = a, r[idx] = r[a];
    l[r[a]] = idx, r[a] = idx ++ ;
}

//删除节点a
void remove(int a)
{
    r[l[a]] = r[a];
    l[r[a]] = l[a];
}

int main()
{
    //0是左端点，1是右端点
    l[1] = 0, r[0] = 1, idx = 2;

    int m;
    cin >> m;
    while (m -- )
    {
        string op;
        int k, x;
        cin >> op;

        if (op == "L")
        {
            cin >> x;
            insert(0, x);
        }
        else if (op == "R")
        {
            cin >> x;
            insert(l[1], x);
        }
        else if (op == "D")
        {
            cin >> k;
            remove(k + 1);
        }
        else if (op == "IL")
        {
            cin >> k >> x;
            insert(l[k + 1], x);
        }
        else 
        {
            cin >> k >> x;
            insert(k + 1, x);
        }
    }

    for (int i = r[0]; i != 1; i = r[i]) cout << e[i] << " ";

    return 0;
}

树与图的深度优先遍历

树的重心

• 树是一种特殊的图，无向图又是特殊的有向图；因此考虑有向图如何存储即可；有向图的存储 ：稠密图->邻接矩阵；邻接表，存储每个点可以到达哪些点
• 图的邻接表存储方式是为每一个结点开个表，存的意思是从这个点可以走到哪些点，这个单链表内部点的顺序是无关紧要的
• n个点所以是n-1条边；cstring头文件；边数这里设置为点数的两倍，在开数组时注意；st数组记录是否遍历过该点，在遍历一个点所有能到达的点的过程中，为了避免走回头路，也要用到st数组；注意当前这颗子树的大小 和 去掉这个点后最大联通块 之间的关系；图用的是多条单链表，所以注意每次都要初始化h数组；无向图，所以add两次；这里随便挑一个点都可以开始dfs，树从哪个点都可以开始当根

#include 
#include 		// memset
#include 

using namespace std;

const int N = 1e5 + 10, M = 2 * N;

int n, m;

// head, e[M],ne[M],idx; 是一条单链表
// h[N], e[M],ne[M],idx; 是N条单链表
int h[N], e[M], ne[M], idx;

bool st[N];  // 用st数组存一下哪些点已经被遍历过了

int ans = N;  //记录一个全局最大值

// 在a对应的单链表中插入一个节点b
void add(int a, int b)
{
    e[idx] = b;         // 表示第idx条边指向b点
    ne[idx] = h[a];  // ne[idx]表示第idx条边的下一条边是 a点的邻接链表的第一条边
    h[a] = idx++;    // head[a]表示将a点的邻接链表的第一条边更新为第idx条边
}

// u表示当前已经dfs到的这个点
// 以u为根的子树中， 点的数量
int dfs(int u)
{
    st[u] = true;  // 标记一下， 当前这个点已经被搜索过

    int sum = 1;  // 记录当前子树大小
    int res = 0;  // 把u这个点删除之后， 每一个联通块的最大值

    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];  // 当前这个链表中的节点， 对应图中的点的编号是多少
        if (!st[j]) {
            int s = dfs(j);     // j这棵子树的大小
            res = max(res, s);  //最大的联通块大小
            sum += s;
        }
    }
    res = max(res, n - sum);
    ans = min(ans, res);
    return sum;
}

int main()
{
    // 一条单链表 head初始化为-1
    // n条单链表，把所有的head初始化为-1
    memset(h, -1, sizeof h);

    cin >> n;
    for (int i = 0; i < n - 1; i++) {
        int a, b;
        cin >> a >> b;
        add(a, b);
        add(b, a);
    }

    // 随便挑一个点， 比方说从第一个点开始搜
    dfs(1);

    cout << ans << endl;

    return 0;
}

树与图的广度优先遍历

图中点的层次

• 建图然后bfs；dist表示距离，-1表示走不到，初始化为-1

#include 
#include 
#include 

using namespace std;

const int N = 1e5 + 10;

int n, m;
int h[N], e[N], ne[N], idx;
int dist[N];

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx ++ ;
}

int bfs()
{
    memset(dist, -1, sizeof dist);
    queue<int> q;

    q.push(1);
    dist[1] = 0;

    while (q.size())
    {
        auto t = q.front();
        q.pop();

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] == -1)
            {
                dist[j] = dist[t] + 1;
                q.push(j);
            }
        }
    }

    return dist[n];
}

int main()
{

    memset(h, -1, sizeof h);

    scanf("%d%d", &n, &m);
    for (int i = 0; i < m; i ++ )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
    }

    printf("%d\n", bfs());
}

拓扑排序

有向图的拓扑序列

• 有向无环图也被称为拓扑图
• 拓扑序列 ：所有的边都从前指向后，那么所有入度为0的点都可以作为起点

#include 
#include 
#include 

using namespace std;

const int N = 1e5 + 10;

int h[N], e[N], ne[N], idx;
int top[N];
int d[N];
int cnt = 0;
int n, m;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

bool topsort()
{
    queue<int> q;
    for (int i = 1; i <= n; i ++ )
        if (!d[i])
            q.push(i);
    
    while (q.size())
    {
        auto t = q.front();
        q.pop();
        top[cnt ++ ] = t;
        
        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            d[j] -- ;
            if (!d[j])
                q.push(j);
        }
    }
    
    return cnt == n;
}

int main()
{
    cin >> n >> m;
    
    memset(h, -1, sizeof h);
    
    for (int i = 0; i < m; i ++ )
    {
        int a, b;
        cin >> a >> b;
        add(a, b);
        d[b] ++ ;
    }
    
    if (!topsort()) puts("-1");
    else
    {
        for (int i = 0; i < n; i ++ )
        {
            cout << top[i];
            if (i != n - 1) cout << ' ';
        }
    }
    
    return 0;
}

#include 
#include 

using namespace std;

const int N = 1e5 + 10;

int h[N], e[N], ne[N], idx;
int q[N];
int d[N];

int n, m;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

bool topsort()
{
    int hh = 0, tt = -1;
    for (int i = 1; i <= n; i ++ )
        if (!d[i])
            q[ ++ tt] = i;
    
    while (hh <= tt)
    {
        auto t = q[hh ++ ];
        
        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            d[j] -- ;
            if (!d[j])
                q[ ++ tt] = j;
        }
    }
    
    return tt + 1 == n;
}

int main()
{
    memset(h, -1, sizeof h);
    
    cin >> n >> m;
    for (int i = 0; i < m; i ++ )
    {
        int a, b;
        cin >> a >> b;
        add(a, b);
        d[b] ++ ;
    }
    
    if (!topsort()) puts("-1");
    else
    {
        for (int i = 0; i < n; i ++ )
        {
            cout << q[i];
            if (i != n - 1) cout << ' ';
        }
    }
    
    return 0;
}

Dijkstra

Dijkstra求最短路 I

• 稠密图，邻接矩阵；稀疏图，邻接表
• 建图时要把所有边初始化为正无穷，，为了应对重边，每次保留最短的边；先将所有距离初始化为正无穷，起点距离为0，遍历n-1轮，每轮确定一个点，找到未标记的点中距离最小的，然后用这个点更新其它点的距离，再标记这个距离最小的点，表示已经用它更新过
• 每个点只能被用来更新其它点一次
• 基于贪心思想，只适用于所有边的长度都是非负数的图

#include 
#include 

using namespace std;

const int N = 510;

int g[N][N];
int dist[N];
bool st[N];

int n, m;

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    for (int i = 0; i < n - 1; i ++ )
    {
        int t = -1;
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        
        for (int j = 1; j <= n; j ++ )
            dist[j] = min(dist[j], dist[t] + g[t][j]);
        
        st[t] = true;
    }
    
    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    memset(g, 0x3f, sizeof g);
    
    cin >> n >> m;
    for (int i = 0; i < m; i ++ )
    {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = min(g[a][b], c);
    }
    
    printf("%d", dijkstra());
    
    return 0;
}

Dijkstra求最短路 II

• 稀疏图 -> 邻接表（相比多了w数组记录权值
• 用邻接表存图，重边无所谓
• priority_queue在queue头文件中，小根堆默认按照第一个权值从小到大排序
• 小根堆的写法
• 每次找全局最小且未被标记过的去更新其它点的dist；所以在每次更新的时候顺便把新的dist和对应的点放进去
• 同上，每一个点只会被用来松弛其它边一次，所以只会进优先队列一次；在松弛其它边的时候，如果松弛成功，就将点进入优先队列

#include 
#include 
#include 
#include 

using namespace std;

const int N = 1e6 + 10;

typedef pair<int, int> pii;

int n, m;
int head[N], e[N], ne[N], idx, w[N];
int dist[N];  //从1号点走到每个点， 当前的最短距离是多少
bool st[N];  //用于在更新最短距离时，判断当前的点的最短距离是否确定，是否需要更新

void add(int a, int b, int c)
{
    e[idx] = b;
    w[idx] = c;
    ne[idx] = head[a];
    head[a] = idx++;
}

// 进行n次迭代后最后就可以确定每个点的最短距离
// 然后再根据题意输出相应的 要求的最短距离
int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;  // 第一个点到自己的距离为0

    priority_queue<pii, vector<pii>, greater<pii>> heap;  //转换为小根堆

    heap.push({0, 1});  //将1号点放进来， 值是0， 编号是1

    while (heap.size()) {
        auto t = heap.top();  //每次找到堆中最小的点
        heap.pop();
        int ver = t.second, distance = t.first;  //距离最小的点的编号和距离

        if (st[ver]) {  //如果这个点被访问过， 就continue
            continue;
        }

        st[ver] = true;

        // 更新当前这个点的所有出边
        for (int i = head[ver]; i != -1; i = ne[i]) {
            int j = e[i];
            if (dist[j] > distance + w[i]) {
                dist[j] = distance + w[i];
                heap.push({dist[j], j});
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) {  // 如果第n个点路径为无穷大即不存在最低路径
        return -1;
    }
    return dist[n];
}

int main()
{
    cin >> n >> m;

    memset(head, -1, sizeof head);

    for (int i = 0; i < m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);  //用邻接表存， 重边就无所谓了
    }

    // 求单源最短路径
    cout << dijkstra() << endl;

    return 0;
}

bellman-ford

有边数限制的最短路

• memcpy(last, dist, sizeof dist)中last数组是上一轮中dist数组的备份，是为了防止串联更新，因为bellmanford是求有边数限制的最短路，而spfa是没有边数限制的，所以不需要拷贝上一轮。
• Bellman - ford 算法是求含负权图的单源最短路径的一种算法，效率较低，代码难度较小。其原理为连续进行松弛，在每次松弛时把每条边都更新一下，若在 n-1 次松弛后还能更新，则说明图中有负环，因此无法得出结果，否则就完成。
• 在下面代码中，是否能到达n号点的判断中需要进行if(dist[n] > INF/2)判断，而并非是if(dist[n] == INF)判断，原因是INF是一个确定的值，并非真正的无穷大，会随着其他数值而受到影响，dist[n]大于某个与INF相同数量级的数即可
• bellman - ford算法擅长解决有边数限制的最短路问题，时间复杂度 O(nm)，其中n为点数，m为边数
• 存边方式独特，边数限制，拷贝上一轮，大于判断

#include 
#include 
#include 

using namespace std;

const int N = 510, M = 10010;

struct Edge
{
    int a, b, c;
} edges[M];

int n, m, k;
int dist[N];
int last[N];

void bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);

    dist[1] = 0;
    for (int i = 0; i < k; i++) {
        memcpy(last, dist, sizeof dist);  //只用上一次迭代的结果
        for (int j = 0; j < m; j++) {
            auto e = edges[j];
            dist[e.b] = min(dist[e.b], last[e.a] + e.c);
        }
    }
}

int main()
{
    cin >> n >> m >> k;

    for (int i = 0; i < m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        edges[i] = {a, b, c};
    }

    bellman_ford();

    if (dist[n] > 0x3f3f3f3f / 2) {
        cout << "impossible" << endl;
    }
    else {
        cout << dist[n] << endl;
    }

    return 0;
}

spfa

spfa求最短路

• spfa被称为队列优化的bellmanford算法，
• 建立一个队列，最初队列中只包含起点；取出队头x，扫描它的所有出边（x，y，z），如果能被松弛，则松弛dist[y]，同时如果y不在队列中，将y放入队列中（每次取出队头的时候也要改变st数组）；
• 一个结点可能被入队，出队多次；这个队列避免了bellmanford算法中对不需要拓展的结点的冗余扫描，在稀疏图上运行效率较高，为$O(km)$级别，k是一个较小的常数，但在稠密图或者特殊构造的网格图上，仍可能退化成$O(nm)$
• st为true的点也可能被再次更新，所以更新的时候不需要判断是否！st
• st数组记录这个点当前是否在队列中
• 队列中都是由起点更新到的点，不存在bellmanford中未更新到的点同样被边更新的情况，所以spfa中等于判断就可以，不像bellman中是大于判断

#include 
#include 
#include 

using namespace std;

const int N = 1e5 + 10;

int n, m;
int head[N], e[N], ne[N], w[N], idx;
bool st[N];
int dist[N];

void add(int a, int b, int c)
{
    e[idx] = b;
    w[idx] = c;
    ne[idx] = head[a];
    head[a] = idx++;
}

int spfa()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    queue<int> q;
    q.push(1);

    st[1] = true;  //判重数组， 队列中有重复的点没有意义

    while (q.size()) {
        int t = q.front();
        q.pop();

        st[t] = false;

        for (int i = head[t]; i != -1; i = ne[i]) {
            int j = e[i];
            if (dist[j] > dist[t] + w[i]) {
                dist[j] = dist[t] + w[i];
                if (!st[j]) {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
    if (dist[n] == 0x3f3f3f3f) {
        return -1;
    }
    return dist[n];
}

int main()
{
    cin >> n >> m;

    memset(head, -1, sizeof head);

    for (int i = 0; i < m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }

    int t = spfa();

    if (t == -1) {
        cout << "impossible" << endl;
    }
    else {
        cout << dist[n] << endl;
    }

    return 0;
}

spfa判断负环

• dist和cnt数组都不需要被初始化，dist数组代表当前从1到x的最短路径长度，cnt数组代表当前从1到x的边的数量
• 一开始就把所有点都放到队列里，只有在松弛的时候才会判断如果不在队列中再把它放入队列中，如果松弛时发现cnt也就是边数>=n，说明点大于n，说明有负权回路

#include 
#include 
#include 

using namespace std;

const int N = 2e3 + 10, M = 1e4 + 10;

int n, m;
int head[N], e[M], ne[M], w[M], idx;
bool st[N];
int dist[N]; //      表示 当前从1 -> x的最短距离
int cnt[N]; //cnt[x] 表示 当前从1 -> x的最短路的边数

void add(int a, int b, int c)
{
    e[idx] = b;
    ne[idx] = head[a];
    w[idx] = c;
    head[a] = idx++;
}

bool spfa(){
    // 这里不需要初始化dist数组为 正无穷/初始化的原因是， 如果存在负环， 那么dist不管初始化为多少， 都会被更新

    queue<int> q;

    //不仅仅是1了， 因为点1可能到不了有负环的点， 因此把所有点都加入队列
    for(int i=1;i<=n;i++){
        q.push(i);
        st[i]=true;
    }

    while(q.size()){
        int t = q.front();
        q.pop();
        st[t]=false;
        for(int i = head[t];i!=-1; i=ne[i]){
            int j = e[i];
            if(dist[j]>dist[t]+w[i]){
                dist[j] = dist[t]+w[i];
                cnt[j] = cnt[t]+1;
                if(cnt[j]>=n){	// 有n条边，则n + 1个点，抽屉原理，有两个点是同一个点，则说明路径上存在环，又因为路径变小，说明存在负环
                    return true;
                }
                if(!st[j]){
                    q.push(j);
                    st[j]=true;
                }
            }
        }
    }
    return false;
}

int main()
{
    cin >> n >> m;
    memset(head, -1, sizeof head);
    for (int i = 0; i < m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }

    if (spfa()) {
        cout << "Yes" << endl;
    }
    else {
        cout << "No" << endl;
    }
    return 0;
}

Floyd

Floyd求最短路

• D[k, i, j]表示“经过若干个编号不超过k的结点“从i到j的最短路径，该问题可划分为两个子问题，经过编号不超过k-1的点从i到j，或者从i先到k再到j，$D[k,i,j]=min(D[k-1,i,j],D[k-1][i][k]+D[k-1][k][j])$，初值为$D[0,i,j]=A[i,j]$，其中A[i,j]是开头定义的邻接矩阵
• 与背包问题的状态转移方程类似，k这一维可被省略$D[i,j]=min(D[i,j],D[i][k]+D[k][j])$，最终D[i][j]就保存了从i到j的最短路长度

#include 
#include 
#include 

using namespace std;

const int N = 210, INF = 1e9;

int n, m, Q;
int d[N][N];

void floyd()
{
    for (int k = 1; k <= n; k++) {
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
            }
        }
    }
}

int main()
{
    cin >> n >> m >> Q;

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            if (i == j) {
                d[i][j] = 0;
            }
            else {
                d[i][j] = INF;
            }
        }
    }
    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        d[a][b] = min(d[a][b], c);
    }

    floyd();

    while (Q--) {
        int a, b;
        cin >> a >> b;

        int t = d[a][b];
        if (t > INF / 2) {
            cout << "impossible" << endl;
        }
        else {
            cout << t << endl;
        }
    }
    return 0;
}

• floyd距离和邻接矩阵中两点之间边的距离用的是同一个数组，
• 这里也可以用0x3f3f3f3f，之所以能用1e9应该是这里的总边长才2e8
• 邻接矩阵的初始化，这里多了个0，值得注意
• 这里仍然是判断大于而不是判断等于，也许还是因为不是从起点更新起的，

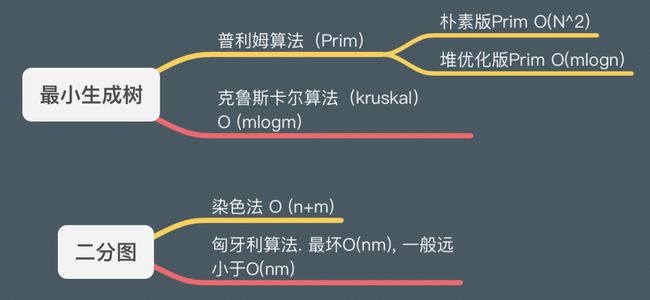
Prim

Prim算法求最小生成树

• $O(n^2)$。堆优化版也不如kruskal方便，所以Prim算法主要用于稠密图，尤其是完全图的最小生成树的求解。
• Prim总是维护最小生成树的一部分。最初，Prim算法仅确定1号节点属于最小生成树；把元素从剩余节点集合中删除，加入到已经属于最小生成树的节点集合中去，并把两个端点分别属于这两个集合中的权值最小的点累加到答案中。
• 可以类别Dijkstra，用一个数组标记节点是否属于集合T，每次从未标记的节点中选择d值最小的，把它标记，同时扫描所有出边，更新另一个端点的d值。

#include 
#include 

using namespace std;

const int N = 510;
const int INF = 0x3f3f3f3f;

int g[N][N];
int dist[N];
bool st[N];
int n, m;

int prim()
{
    memset(dist, 0x3f, sizeof dist);
    
    int res = 0;
    dist[1] = 0;
    
    for (int i = 0; i < n; i ++ )
    {
        int t = -1;
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        
        if (i && dist[t] == INF)		// 如果i为0不用
            return INF;
        
        st[t] = true;		// 标记
        
        if (i) res += dist[t];		// 如果i为0不用累加
        
        for (int j = 1; j <= n; j ++ )
            dist[j] = min(dist[j], g[t][j]);		// 是与g做比较，因为t已经是最小生成树里的了
    }
    
    // 返回累加答案
    return res;
}

int main()
{
    cin >> n >> m;
    
    memset(g, 0x3f, sizeof g);
    
    while (m -- )
    {
        int u, v, w;
        cin >> u >> v >> w;
        g[u][v] = g[v][u] = min(g[u][v], w);
    }
    
    int t = prim();
    
    if (t == INF) puts("impossible");
    else cout << t << endl;
    
    return 0;
}

Kruskal

Kruskal算法求最小生成树

• 从边带权的无向图中选n个点和n-1条本来就有的边构成的无向连通子图称为生成树，在此基础上边的权值之和最小的称为最小生成树
• 定理 ：任意一颗最小生成树一定包含无向图中权值最小的边
• Kruskal算法总是维护无向图的最小生成森林
• 在任意时刻，Kruskal算法从剩余的边中选一条权值最小的，并且这条边的两个端点属于生成森林中两颗不同的树（不连通），把该边加入该森林。图中节点的连通情况可以用并查集维护
• 流程 ：建立并查集；把所有边按权值排序从小到大，依次扫描每条边；若两个端点属于同一个集合，则忽略这条边；否则，合并两个端点所在的集合，并将权值累加到答案中
• 虽然Kruskal算法的时间复杂度局限在于它第一步要使用的库里的快排，o(mlog(m))，但快排常数非常小，所以Kruskal很快

#include 
#include 

using namespace std;

const int N = 1e5 + 10, M = 2e5 + 10, INF = 0x3f3f3f3f;
int n, m;
int fa[N];

struct Edge
{
    int a, b, w;
    
    bool operator< (const Edge &W) const
    {
        return w < W.w;
    }
}edges[M];

int find(int x)
{
    if (fa[x] != x) fa[x] = find(fa[x]);
    return fa[x];
}

int kruskai()
{
    for (int i = 1; i <= n; i ++ ) fa[i] = i;		// 初始化并查集
    
    int res = 0, cnt = 0;1
    
    for (int i = 0; i < m; i ++ )
    {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;
        
        a = find(a), b = find(b);
        if (a != b)
        {
            res += w;
            cnt ++ ;
            fa[a] = b;
        }
    }
    
    if (cnt < n - 1) return INF;
    return res;
}

int main()
{
    cin >> n >> m;
    for (int i = 0; i < m; i ++ )
        cin >> edges[i].a >> edges[i].b >> edges[i].w;
    
    sort(edges, edges + m);		// 排序
    
    int t = kruskai();
    
    if (t == INF)
        puts("impossible");
    else
        cout << t;
    
    return 0;
}

染色法判定二分图

染色法判定二分图

• 二分图 ：当且仅当图中没有奇数环，划分为两个集合，集合内部没有边

#include 
#include 
#include 

using namespace std;

const int N = 1e5 + 10, M = 2 * N;		// 无向图，边存两次，数组两倍

int h[N], e[M], ne[M], idx;
int co[N];
int n, m;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

bool dfs(int u, int c)
{
    co[u] = c;
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!co[j] && !dfs(j, 3 - c))
            return false;
        else if (co[j] == c)
            return false;
    }
    return true;
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 0; i < m; i ++ )
    {
        int u, v;
        cin >> u >> v;
        add(u, v);
        add(v, u);		// 无向图
    }
    
    bool success = true;
    
    for (int i = 1; i <= n; i ++ )		// 图可能不连通
        if (!co[i] && !dfs(i, 1))
        {
            success = false;
            break;
        }
    
    if (success) puts("Yes");
    else puts("No");
    
    return 0;
}

匈牙利算法

二分图的最大匹配

• “任意两条边都没有公共端点”的边的集合被称为图的一组匹配。在二分图中，包含边数最多的一组匹配被称为二分图的最大匹配。
• 二分图的一组匹配S是最大匹配，当且仅当图中不再存在S的增广路
  
• 匈牙利算法基于贪心思想，当一个点成为匹配点后，最多因为增广路而更换匹配对象，不会再变回非匹配点
• 对于每个左部节点，寻找增广路最多遍历整张二分图一次，所以$O(nm)$

#include 
#include 

using namespace std;

const int N = 510, M = 1e5 + 10;

int h[N], e[M], ne[M], idx;
bool st[N];     // st数组代表对于当前左部节点，右部的这个节点在它这轮的匹配中是否被“询问”过;在同一轮中不要重复询问同一个点
int match[N];
int n1, n2, m;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

bool find(int x)
{
    for (int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i];
        
        if (!st[j])
        {
            st[j] = true;
            if (match[j] == 0 || find(match[j]))
            {
                match[j] = x;
                return true;
            }
        }
    }
    return false;
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n1 >> n2 >> m;
    
    for (int i = 0; i < m; i ++ )
    {
        int a, b;
        cin >> a >> b;
        add(a, b);
//        add(b, a);        从左部匹配右部，所以即使无向图，加了会wa
    }
    
    int res = 0;
    
    for (int i = 1; i <= n1; i ++ )
    {
        memset(st, 0, sizeof st);
        if (find(i)) res ++ ;
    }
    
    cout << res << endl;
    
    return 0;
}