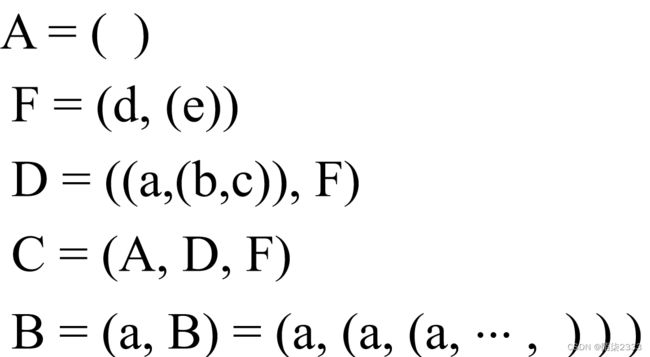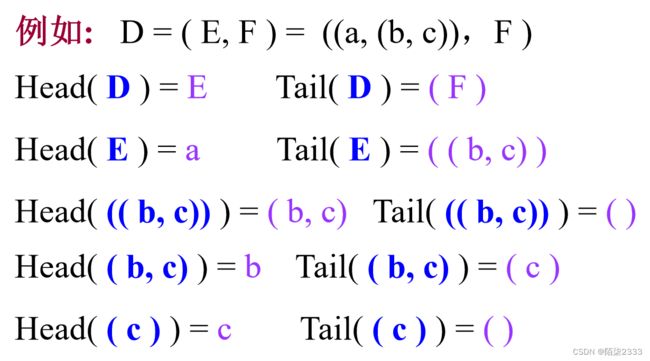数据结构（超详细讲解！！）第二十二节 广义表

1.定义

广义表，顾名思义，也是线性表的一种推广。广义表被广泛地应用于人工智能等领域的表处理语言LISP语言中。在LISP语言中，广义表是一种最基本的数据结构，就连LISP 语言的程序也表示为一系列的广义表。

广义表又称列表，是n ( n 大于等于 0 ) 个元素的有限序列，记作A = ( a1, a2, …, an )。其中A是列表的名字，n是它的长度，ai可以是数据元素，也可以是列表。如果ai是列表，则称其为列表A的子表。

习惯上，用大写字母表示列表的名称，用小写字母表示数据元素。用圆括号把列表的元素括起来，用逗号分隔开列表中的元素。

在广义表GL=(d1, d2，d3，…，dn)中，d1是广义表GL的表头，而广义表GL其余部分组成的表（d2，d3，…，dn）称为广义表的表尾。由此可见广义表的定义是递归定义的，因为在定义广义表时又使用了广义表的概念。

广义表是递归定义的线性结构， GL=(d1, d2，d3，…，dn) 其中：di  或为原子或为广义表

广义表是一个多层次的线性结构

列表的深度 ：列表展开后的最大括号层次数。

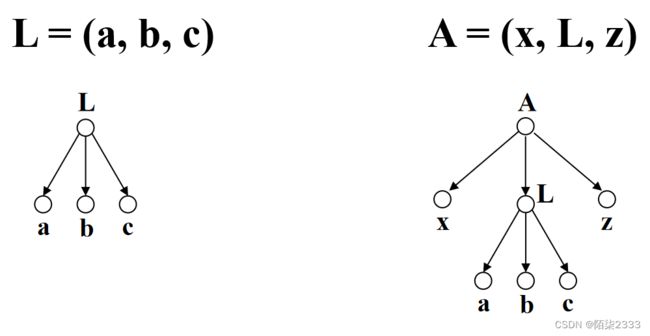
L = (a, b, c)    列表L长度为3，深度为1

E = ( )            E为空表，长度为0，深度为1

A = (x, L, z)   列表A的长度为3，深度为2

B = (A, y, E)  列表B的长度为3，深度为3

C = (A, B)     列表C的长度为2，深度为4

D = (z, D)      列表D的长度为2，深度为无穷大

列表是非终端结点（即交叉结点），数据元素是终端结点，空表作为一个特殊的终端结点。

纯表：通常把与树对应的列表称为纯表，它限制了表中成分的共享性和递归。例如列表L、A、B。

具有共享和递归特性的列表可以和有向图建立对应。

广义表 GL=(d1, d2，d3，…，dn)的结构特点:

1)  广义表中的数据元素有相对次序；

2)  广义表的长度定义为最外层包含元素个数；

3)  广义表的深度定义为所含括弧的重数；    

注意：“原子”的深度为 0               “空表”的深度为 1

4)  广义表可以共享；

5)  广义表可以是一个递归的表。      

递归表的深度是无穷值，长度是有限值。

6）任何一个非空广义表 GL=(d1, d2，d3，…，dn)    均可分解为            

表头  Head(GL) = d1   和   表尾  Tail(GL) = ( d2, …, dn) 两部分。

任何一个非空广义表的表头是表中第一个元素，可以是数据元素，也可以是子表，而其表尾一定是子表。

L = (a, b, c)       E = ( )     A = (x, L, z)      B = (A, y, E)     C = (A, B)      D = (z, D)

head(L) = a,  tail(L) = (b, c)

head(B) = A, tail(B) = (y, E)

head(tail(L)) = head(b, c) = b

tail(tail(tail(L))) = tail(tail(b, c)) = tail(c) = ( )