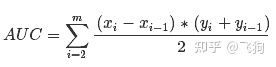第二十九章 目标检测中的测试模型评价指标(车道线感知)

前言

近期参与到了手写AI的车道线检测的学习中去，以此系列笔记记录学习与思考的全过程。车道线检测系列会持续更新，力求完整精炼，引人启示。所需前期知识，可以结合手写AI进行系统的学习。

介绍

自动驾驶的一大前提是保证人的安全，故对人的检测是必须的。考虑到自动驾驶的场景需求，各类车辆、交通灯、交通标志以及其他路上高频出现的，对决策有影响的物体类别都应进行识别，例如摩托车、自行车等。在确定了数据集及检测类别后，测试指标对评估模型性能好坏有着至关重要的意义，目前已有大量相关研究。本文对在工程中选取的指标做出总结，并介绍了目前比较主流的各类评价指标。

测试指标的选取

目标检测问题，一般的常用评价指标有：

• 精度评价指标：map（平均准确度均值，精度评价），准确率 （Accuracy），混淆矩阵 （Confusion Matrix），精确率（Precision），召回率（Recall），平均正确率（AP），mean Average Precision(mAP)，交除并（IoU），ROC + AUC，非极大值抑制（NMS）。
• 速度评价指标： FPS（即每秒处理的图片数量或者处理每张图片所需的时间，当然必须在同一硬件条件下进行比较）

选取mAP、混淆矩阵、PR曲线、fppi和F1-Score作为精度评价指标，其中mAP、F1-Score是量化的评价指标，fppi可以进行量化，使用log-average miss rate作为其量化的评价指标。混淆矩阵和PR曲线从不同角度反映了模型的好坏。

选取FLOPs作为速度评价指标，表征了处理一帧图像所需的计算量，相比FPS更加通用，同时考虑到模型的评价是在同一台主机上进行的，故FPS也将作为参考标准。

下面具体介绍目标检测领域中常用的评价指标。

精度评价指标

MAP（平均准确度均值）

mAP定义及相关概念

• mAP: mean Average Precision, 即各类别AP的平均值
• AP: PR曲线下面积，后文会详细讲解
• PR曲线: Precision-Recall曲线
• Precision: TP / (TP + FP)
• Recall: TP / (TP + FN)
• TP （True Positive，真阳性）：检测器给出正样本，事实上也是正样本，即正确检测到目标
• TN （True Negative，真阴性）：检测器给出负样本，事实上也是负样本，即正确检测到非目标
• FP （False Positive，假阳性）：检测器给出正样本，事实上却是负样本，即误检测
• FN （False Negative，假阴性）：检测器给出负样本，事实上却是正样本，即漏检测
• TP: IoU>0.5的检测框数量（同一Ground Truth只计算一次）
• FP: IoU<=0.5的检测框，或者是检测到同一个GT的多余检测框的数量
• FN: 没有检测到的GT的数量

注意：

（1）一般来说mAP针对整个数据集而言的；

（2）AP针对数据集中某一个类别而言的；

（3）而percision和recall针对单张图片某一类别的。

mAP的具体计算

• 不同数据集map计算方法

由于map是数据集中所有类别AP值得平均，所以我们要计算map，首先得知道某一类别的AP值怎么求。不同数据集的某类别的AP计算方法大同小异，主要分为三种：

（1）在VOC2010以前，只需要选取当Recall >= 0, 0.1, 0.2, …, 1共11个点时的Precision最大值，然后AP就是这11个Precision的平均值，map就是所有类别AP值的平均。

（2）在VOC2010及以后，需要针对每一个不同的Recall值（包括0和1），选取其大于等于这些Recall值时的Precision最大值，然后计算PR曲线下面积作为AP值，map就是所有类别AP值的平均。

（3）COCO数据集，设定多个IOU阈值（0.5-0.95,0.05为步长），在每一个IOU阈值下都有某一类别的AP值，然后求不同IOU阈值下的AP平均，就是所求的最终的某类别的AP值。

• 计算某一类别的AP

由上面概念我们知道，我们计算某一类别AP需要需要绘画出这一类别的PR曲线，所以我们要计算数据集中每张图片中这一类别的percision和recall。

由公式：

• Precision: TP / (TP + FP)
• Recall: TP / (TP + FN)

只需要统计出TP，FP，FN个数就行了。

• 如何判断TP,FP,FN（重要）

拿单张图片来说吧，

• 首先遍历图片中ground truth对象，
• 然后提取我们要计算的某类别的gt objects，
• 之后读取我们通过检测器检测出的这种类别的检测框（其他类别的先不管），
• 接着过滤掉置信度分数低于置信度阈值的框（也有的未设置信度阈值），
• 将剩下的检测框按置信度分数从高到低排序，最先判断置信度分数最高的检测框与gt bbox的iou是否大于iou阈值，
• 若iou大于设定的iou阈值即判断为TP，将此gt_bbox标记为已检测（后续的同一个GT的多余检测框都视为FP,这就是为什么先要按照置信度分数从高到低排序，置信度分数最高的检测框最先去与iou阈值比较，若大于iou阈值，视为TP，后续的同一个gt对象的检测框都视为FP），
• iou小于阈值的，直接规划到FP中去。

这里置信度分数不同的论文可能对其定义不一样，一般指分类置信度的居多，也就是预测框中物体属于某一个类别的概率。

• 计算mAP在NMS之后

这一点一定要明确，**mAP值计算在NMS之后进行的，**mAP是统计我们的检测模型的最终评价指标，是所有操作完成之后，以最终的检测结果作为标准，来计算mAP值的，另外提一点一般只有测试的时候才会作NMS，训练的时候不进行NMS操作，因为训练的时候需要大量的正负样本去学习。

准确率 （Accuracy）

分对的样本数除以所有的样本数 ，即：

准确（分类）率 = 正确预测的正反例数 / 总数。

准确率一般用来评估模型的全局准确程度，不能包含太多信息，无法全面评价一个模型性能。

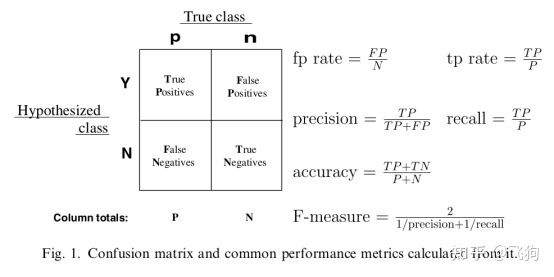
混淆矩阵 （Confusion Matrix）

混淆矩阵中的横轴是模型预测的类别数量统计，纵轴是数据真实标签的数量统计。

对角线，**表示模型预测和数据标签一致的数目，*所以对角线之和除以测试集总数就是*准确率。对角线上数字越大越好，在可视化结果中颜色越深，说明模型在该类的预测准确率越高。如果按行来看，每行不在对角线位置的就是错误预测的类别。总的来说，我们希望对角线越高越好，非对角线越低越好。

精确率（Precision）与召回率（Recall）

一些相关的定义。假设现在有这样一个测试集，测试集中的图片只由大雁和飞机两种图片组成，假设你的分类系统最终的目的是：能取出测试集中所有飞机的图片，而不是大雁的图片。

• True positives : 正样本被正确识别为正样本，飞机的图片被正确的识别成了飞机。
• True negatives: 负样本被正确识别为负样本，大雁的图片没有被识别出来，系统正确地认为它们是大雁。
• False positives: 假的正样本，即负样本被错误识别为正样本，大雁的图片被错误地识别成了飞机。
• False negatives: 假的负样本，即正样本被错误识别为负样本，飞机的图片没有被识别出来，系统错误地认为它们是大雁。
• **Precision其实就是在识别出来的图片中，True positives所占的比率。**也就是本假设中，所有被识别出来的飞机中，真正的飞机所占的比例。

• Recall 是测试集中所有正样本样例中，被正确识别为正样本的比例。也就是本假设中，被正确识别出来的飞机个数与测试集中所有真实飞机的个数的比值。

• **Precision-recall 曲线：**改变识别阈值，使得系统依次能够识别前K张图片，阈值的变化同时会导致Precision与Recall值发生变化，从而得到曲线。

如果一个分类器的性能比较好，那么它应该有如下的表现：

在Recall值增长的同时，Precision的值保持在一个很高的水平。

而性能比较差的分类器可能会损失很多Precision值才能换来Recall值的提高。

通常情况下，文章中都会使用Precision-recall曲线，来显示出分类器在Precision与Recall之间的权衡。

平均精度（Average-Precision，AP）与 mean Average Precision(mAP)

AP就是Precision-recall 曲线下面的面积，通常来说一个越好的分类器，AP值越高。

mAP是多个类别AP的平均值。这个mean的意思是对每个类的AP再求平均，得到的就是mAP的值，mAP的大小一定在[0,1]区间，越大越好。该指标是目标检测算法中最重要的一个。

在正样本非常少的情况下，PR表现的效果会更好。

IoU

IoU这一值，可以理解为系统预测出来的框与原来图片中标记的框的重合程度。

计算方法即检测结果Detection Result与 Ground Truth 的交集比上它们的并集，即为检测的准确率。

IOU正是表达这种bounding box和groundtruth的差异的指标：

ROC（Receiver Operating Characteristic）曲线与AUC（Area Under Curve）

受试者工作特征曲线 (receiver operating characteristic curve，简称ROC曲线)，又称为感受性曲线(sensitivity curve)。

ROC空间将伪阳性率（FPR）定义为 X 轴，真阳性率（TPR）定义为 Y 轴。

ROC曲线：

• 横坐标：假正率(False positive rate， FPR)，FPR = FP / [ FP + TN] ，代表所有负样本中错误预测为正样本的概率，假警报率；
• 纵坐标：真正率(True positive rate， TPR)，TPR = TP / [ TP + FN] ，代表所有正样本中预测正确的概率，命中率。

PD=(number of true target)/(number of actural target)

FA=number of false detection/number of tested frames

以FA为横轴PD为纵轴绘制ROC曲线

对角线对应于随机猜测模型，而（0,1）对应于所有整理排在所有反例之前的理想模型。

曲线越接近左上角，分类器的性能越好。

ROC曲线有个很好的特性：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。

在实际的数据集中经常会出现类不平衡（class imbalance）现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化。

ROC曲线绘制：

（1）根据每个测试样本属于正样本的概率值从大到小排序；

（2）从高到低，依次将“Score”值作为阈值threshold，当测试样本属于正样本的概率大于或等于这个threshold时，我们认为它为正样本，否则为负样本；

（3）每次选取一个不同的threshold，我们就可以得到一组FPR和TPR，即ROC曲线上的一点。

当我们将threshold设置为1和0时，分别可以得到ROC曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来，就得到了ROC曲线。当threshold取值越多，ROC曲线越平滑。

• AUC（Area Under Curve）

即为ROC曲线下的面积。AUC越接近于1，分类器性能越好。

**物理意义：**首先AUC值是一个概率值，当你随机挑选一个正样本以及一个负样本，当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值。当然，AUC值越大，当前的分类算法越有可能将正样本排在负样本前面，即能够更好的分类。

计算公式：就是求曲线下矩形面积。

• PR曲线和ROC曲线比较

——ROC曲线特点：

（1）优点：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。因为TPR聚焦于正例，FPR聚焦于与负例，使其成为一个比较均衡的评估方法。

在实际的数据集中经常会出现类不平衡（class imbalance）现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化。

（2）缺点：上文提到ROC曲线的优点是不会随着类别分布的改变而改变，但这在某种程度上也是其缺点。因为负例N增加了很多，而曲线却没变，这等于产生了大量FP。像信息检索中如果主要关心正例的预测准确性的话，这就不可接受了。在类别不平衡的背景下，负例的数目众多致使FPR的增长不明显，导致ROC曲线呈现一个过分乐观的效果估计。ROC曲线的横轴采用FPR，根据FPR ，当负例N的数量远超正例P时，FP的大幅增长只能换来FPR的微小改变。结果是虽然大量负例被错判成正例，在ROC曲线上却无法直观地看出来。（当然也可以只分析ROC曲线左边一小段）

——PR曲线：

（1）PR曲线使用了Precision，因此PR曲线的两个指标都聚焦于正例。类别不平衡问题中由于主要关心正例，所以在此情况下PR曲线被广泛认为优于ROC曲线。

使用场景：

1. ROC曲线由于兼顾正例与负例，所以适用于评估分类器的整体性能，相比而言PR曲线完全聚焦于正例。
2. 如果有多份数据且存在不同的类别分布，比如信用卡欺诈问题中每个月正例和负例的比例可能都不相同，这时候如果只想单纯地比较分类器的性能且剔除类别分布改变的影响，则ROC曲线比较适合，因为类别分布改变可能使得PR曲线发生变化时好时坏，这种时候难以进行模型比较；反之，如果想测试不同类别分布下对分类器的性能的影响，则PR曲线比较适合。
3. 如果想要评估在相同的类别分布下正例的预测情况，则宜选PR曲线。
4. 类别不平衡问题中，ROC曲线通常会给出一个乐观的效果估计，所以大部分时候还是PR曲线更好。
5. 最后可以根据具体的应用，在曲线上找到最优的点，得到相对应的precision，recall，f1 score等指标，去调整模型的阈值，从而得到一个符合具体应用的模型。

fppi/fppw

• fppi = false positive per image

OK，到这里你好不容易画出PR曲线，算好了mAP，然后兴高采烈的在项目进度会上大讲特讲。当你说完后，对面的产品妹子，用看智障的眼神瞅了你一眼，不紧不慢的说：
我不关心什么mAP，更不关心你的曲线，我就想知道你这个算法平均每张图错几个。

fppi曲线

fppi曲线的纵轴为FN（即Miss rate），横轴为false positive per image。

显然相比PR曲线，fppi更接近于实际应用。

至于画法，与PR曲线类似，都是通过调整thresh_conf计算相关指标画点，然后连线得到。
对应的还有fppw(fppw = false positive per window)。

在介绍miss rate versus false positives per-image（后文简称FPPI）之前，就不得不先说另一个指标，名字叫
miss rate versus false positives per window（后文简称FPPW） 。

起初呢，大家是使用FPPW作为评价行人检测指标的。这个指标最早出现在文章 Histograms of Oriented Gradients for Human Detection。这篇文章中发表了INRIA行人数据集，评估性能的时候就是用这个FPPW（值得一提的是，HOG+SVM这个经典的行人检测方法也是在这篇文章中提出的）

下面简单介绍下FPPW的检测原理：

FPPW的纵轴是miss rate，横轴是false positives per window，两个坐标轴都是采用对数坐标轴表示：

miss rate = false negative / positive，即1-recall，即表示所有存在的行人中（positive），漏检的行人（false negative）占了多少
false positives per window = false positive / the number of window
为什么要用the number of window呢，因为这和HOG+SVM的原理相关，他的检测过程大概是这样的：

输入一张待检测的图片
首先用滑窗法，选取图片上的某一块区域（后面称这块区域为window）
提取这个区域的HOG特征
将HOG特征输入SVM中，利用SVM进行分类，判断是否为行人
通过上面的过程我们可以看到，因为SVM仅仅只是作为分类器，所以如果要检测到不同size的行人的话，就需要在滑窗法中用很多不同size的窗口去滑动，每滑动一次，就对应一个window，因此诞生了很多window，每个window都对应一个SVM的预测结果。

对于一张图片来说，我们关注的是SVM是否能够对这些window判断准确，所以用false positive / the number of window，就可以评估SVM在这张图片上的检测性能如何。

那如何得到多个miss rate与fppw值呢？

这和ROC曲线的套路比较类似，即通过调整检测的阈值，来得到一系列的miss rate与fppw。

例如，阈值越高，说明只有置信度越高的检测框才能被认为是检测器的输出，所以输出的实际检测框越少、检测框越准确，检测到空气的可能性越低，这也会导致漏检概率越大（置信度低的true positive变为了false negative），所以此时miss rate增加，fppw减少。反之同理。

上面是只有一个图片时的计算方法，对于多张的图片来说，其实也是类似的。首先先把所有图片的结果都放在一起，按照置信度由高到低排序，然后按照置信度的高低来调整检测的阈值，由此就得到了一系列的miss rate与fppw，然后再除以the number of window（此时the number of window为每张图片上window的数量*图片的数量）。

（调整检测的阈值的例子在下文中有）

那FPPW如何量化对比呢？

因为曲线与曲线之间是没办法量化对比的，所以作者使用FPPW=1 0 − 4 时 10^{−4}时10
−4
时的miss rate作为结果对比的参考点（地位类似ROC曲线中的AUC值）。

以上，就是FPPW的大致原理。

原文中，作者说FPPW这个指标对于miss rate变化非常敏感，即miss rate稍微变化一点点，横轴的fppw就会改变非常大。例如，miss rate每降低1％，就相当于将原本的fppw降低1.57倍。

miss rate versus false positives per image (FPPI)

前面介绍了FPPW，但是FPPW存在以下问题：

不能反映false positive在不同size和位置空间中的表现，即无法得知分类器检测目标附近的表现或分类器在与目标相似的背景下性能如何。
因为我们从per window中无法得知这个window是在图像中哪个位置的，也无法得知这个window的size如何，我们用per window所能得到关于window的有用信息量也不大，所以per window并没有什么特别优势
FPPW这个指标不好理解，因为per window这个概念过于接近底层的检测原理了，按照正常的思维，我们其实比较好奇的是 “对于每一张图片，误检率是多少”，我们会思考更加宏观、贴近实际应用的场景，反而不会关心每个window检测情况是怎样
所以在文章Pedestrian detection: A benchmark中，作者提出了FPPI作为更合适的行人检测衡量指标。

FPPI的好处主要如下：

per image这个概念更加贴近实际生活，更好理解
下面简单介绍下FPPI的检测原理：

FPPI的纵轴是miss rate，横轴是false positives per image，两个坐标轴都是采用对数坐标轴表示：

miss rate = false negative / positive，即1-recall
false positives per image = false positive / the number of image
我们可以发现，其实就只是横轴变了而已，其实纵轴是一样的。

同样，我们也可以调整阈值，得到一系列的miss rate和fppi。

那FPPI如何量化对比呢？

同样，曲线与曲线之间是没办法量化对比的，所以一开始，使用FPPI=1时的miss rate作为结果对比的参考点。

但是在后续的论文 Pedestrian Detection: An Evaluation of the State of the Art中（两篇论文的作者都是大神Piotr Dollar），作者改成了使用log-average miss rate作为结果对比的参考点，计算方式为：

在对数坐标系下，从 1 0 − 2 10^{-2} 10−2到 1 0 0 10^0 100之间均匀地取9个FPPI值，这9个FPPI值会对应9个miss rate值，将这9个miss rate值求均值，就得到了log-average miss rate。

（对于一些在达到特定FPPI值之前，就已经提前结束的曲线，miss rate值则取曲线所能达到的最小值）

什么叫提前结束的曲线呢？

我们可以看看下面这张图

倒数第二个紫色的HogLbp还没有达到 1 0 0 10^0 100就已经提前结束了，而且你也会发现不同曲线也是长短不一，为什么会这样呢？其实这和不同检测器的输出有关。

因为FPPI图中的曲线本质上是由一组一组的[fppi,mr]点组成的，这些点就连成了曲线，曲线提前结束了，说明这些点的最大fppi值到不了 1 0 0 10^0 100 。而一组一组的[fppi,mr]点是通过调整检测器的阈值得到的。检测器的阈值选取方式，是根据检测器输出检测框的数量和置信度决定的。

例如，检测器A检测了3张图片，它在这3张图片上共输出了10个检测框，每个检测框有其对应的置信度，我们按照置信度将这些检测框由高到低排序，例如：0.9、0.85、0.8、0.75、0.7、0.65、0.6、0.55、0.5、0.45。

我们先选择0.9作为检测器的阈值，大于等于0.9的检测框，我们认为有行人、低于0.9的检测框，我们认为没有行人，这样我们就得到了一个[fppi,mr]点。

接下来，我们选择0.85作为检测器的阈值，大于等于0.85的检测框，我们认为有行人、低于0.85的检测框，我们认为没有行人，这样我们就得到了一个[fppi,mr]点。

以此类推，一直到0.45，我们就可以一共得到10个[fppi,mr]点，即检测器输出了多少个检测框，我们就能得到多少个[fppi,mr]点。当阈值为0.45时，假设检测器A对应的[fppi,mr]点的值为[0.8, 0.25]，那么此时，检测器A的曲线最多只能画到fppi=0.8，所以就到不了 1 0 0 10^0 100 了。但是如果换了一个检测器，可能他们输出的检测框结果。例如，检测器B检测同样的3张图片，假设它在这3张图片上也是共输出了10个检测框，按照上面的步骤，检测器B就会输出10个[fppi,mr]点。当阈值为0.45时，假设检测器B对应的[fppi,mr]点的值为[1.5, 0.25]，那么此时，检测器B的曲线在绘制的时候就会超出 1 0 0 10^0 100 。

（不同检测器输出的检测框数量可能也不一样，也是一个影响因素，为了简化表述所以上面的例子中没有考虑进去）

其实说白了，就是不同检测器性能不一样。当检测器的阈值选择最低的那个置信度时，本质上就是所有的检测框我们都认为检测结果为行人，此时如果有些检测器有很多误检的框，那么它所能达到的fppi就会比较高；如果有些检测器误检的框比较少，那么它所能达到的fppi最大值也会比较低，所以因此导致了不同检测器的fppi上界不同。

以上，就是FPPI的大致原理。

由ROC曲线得到FPPI曲线
在实际画FPPI曲线的代码中，作者用的是compRoc、plotRoc这些带有ROC字眼的词来写的，那我们从理论上来看看作者是怎么通过ROC得到FPPI的

ROC曲线的y轴是TPR（True positive rate），x轴是FPR（False positive rate）：

TPR = TP / ( TP + FN )
FPR = FP / ( FP + TN )
TPR 和recall的计算公式是一样，所以我们可以认为TPR=recall

FPPI曲线的y轴是miss rate，x轴是fppi（false positives per image）：

miss rate = FN / ( TP + FN )
fppi = FP / the number of image
关于y轴的转换

miss rate = ( TP + FN - TP) / ( TP + FN ) = 1 - recall = 1 - TPR

所以只要用1减去ROC曲线的y值，就可以得到FPPI曲线的y值

关于x轴的转换

作者在compRoc函数中，对于ROC曲线，计算的y轴就是fppi！这其实是一个名词理解的问题。。。。

通常，我们一听到ROC曲线，想到的就是y轴是TPR、x轴是FPR的曲线。

但是在作者的代码中，他所指代的ROC，指的是y轴是TPR、x轴是fppi的曲线。所以不存在类似y轴一样的FPR与fppi之间的转换，因为作者直接算的就是fppi

我们也可以换一个角度理解他为什么要这样命名，其实ROC曲线的FPR和FPPI曲线中的fppi他们的本质是非常相近的，分子都是FP，这两个指标关注的都是误检方面。

两者的区别只是在于分母不同，FPR的分母是“所有负例”，fppi的分母是“所有图片”。

这也是很好理解的，因为在行人检测任务中，“所有负例”的数量实在是太多了！一张图片就只有那么几个行人（即“正例”），没有行人的地方都可以认为是“负例”，这个数量我们是确定不了的。

所以在行人检测任务中，FPR是算不出来的，所以用的是fppi来评价误检的情况。

非极大值抑制（NMS）

Non-Maximum Suppression就是需要根据score矩阵和region的坐标信息，从中找到置信度比较高的bounding box。对于有重叠在一起的预测框，只保留得分最高的那个。

（1）NMS计算出每一个bounding box的面积，然后根据score进行排序，把score最大的bounding box作为队列中首个要比较的对象；

（2）计算其余bounding box与当前最大score与box的IoU，去除IoU大于设定的阈值的bounding box，保留小的IoU得预测框；

（3）然后重复上面的过程，直至候选bounding box为空。

最终，检测了bounding box的过程中有两个阈值，一个就是IoU，另一个是在过程之后，从候选的bounding box中剔除score小于阈值的bounding box。需要注意的是：Non-Maximum Suppression一次处理一个类别，如果有N个类别，Non-Maximum Suppression就需要执行N次。

F1-Score

F1分数(F1-score)是分类问题的一个衡量指标。F1分数认为召回率和精度同等重要, 一些多分类问题的机器学习竞赛，常常将F1-score作为最终测评的方法。它是精确率和召回率的调和平均数，最大为1，最小为0。计算公式如下：

F1= 2TP/(2TP+FP+FN)

此外还有F2分数和F0.5分数。F2分数认为召回率的重要程度是精度的2倍，而F0.5分数认为召回率的重要程度是精度的一半。计算公式为：

更一般地，我们可以定义Fβ（precision和recall权重可调的F1 score）:

Fβ = ((1+β*β)*precision*recall) / (β*β*precision + recall)

常用的如F2和F0.5。

速度评价指标

概述

目标检测技术的很多实际应用在准确度和速度上都有很高的要求，如果不计速度性能指标，只注重准确度表现的突破，但其代价是更高的计算复杂度和更多内存需求，对于全面行业部署而言，可扩展性仍是一个悬而未决的问题。一般来说目标检测中的速度评价指标有：

（1）FPS，检测器每秒能处理图片的张数

（2）检测器处理每张图片所需要的时间

但速度评价指标必须在同一硬件上进行，同一硬件，它的最大FLOPS（每秒运算浮点数代表着硬件性能，此处区分FLOPs）是相同的，不同网络，处理每张图片所需的FLOPs(浮点操作数)是不同的，所以同一硬件处理相同图片所需的FLOPs越小，相同时间内，就能处理更多的图片，速度也就越快，处理每张图片所需的FLOPs与许多因素有关，比如你的网络层数，参数量，选用的激活函数等等，这里仅谈一下网络的参数量对其的影响，一般来说参数量越低的网络，FLOPs会越小，保存模型所需的内存小，对硬件内存要求比较低，因此比较对嵌入式端较友好。

• 一般来说ResNeXt+Faster RCNN在NVIDIA GPU上可以做到1秒/图
• 而MobileNet+SSD在ARM芯片上可以做到300毫秒/图

ARM和GPU之间的运算能力差距，各位都懂。

FLOPs计算

• FLOPs和FLOPS区分

先解释一下FLOPs：floating point operations 指的是浮点运算次数，理解为计算量，可以用来衡量算法/模型的复杂度。

此处区分一下FLOPS（全部大写），FLOPS指的是每秒运算的浮点数，理解为计算速度，衡量一个硬件的标准。我们要的是衡量模型的复杂度的指标，所以选择FLOPs。

• FLOPs计算（以下计算FLOPs不考虑激活函数的运算）

(1)卷积层

FLOPs=(2*Ci*k*K-1）*H*W*Co（不考虑bias）

FLOPs=(2*Ci*k*K）*H*W*Co（考虑bias）

Ci为输入特征图通道数，K为过滤器尺寸，H,W,Co为输出特征图的高，宽和通道数。

最后得到的Co张输出特征图，每张特征图上有HW个像素点，而这其中的每个像素点的值都是由过滤器与输入特征图卷积得到的，过滤器中Cik*K个点，每个点都要和输入特征图对应点作一次相乘操作（浮点操作数为 c i × k × k c_i \times k\times k ci×k×k），然后将这些过滤器和输入特征图对应点相乘所得的数相加起来（浮点操作数为 c i × k × k c_i \times k\times k ci×k×k，n个数相加，所需要的浮点操作数为n-1），得到一个值，对应于一张输出特征图中的一个像素，输出特征图有Co张，故有Co个过滤器参与卷积运算，所以卷积层的 F L O P s = ( 2 × C i × k × k − 1 ) × H × W × C o FLOPs=(2\times C_i \times k \times k -1)\times H \times W \times C_o FLOPs=(2×Ci×k×k−1)×H×W×Co

(Ci为输入特征图通道数，K为过滤器尺寸，H,W,Co为输出特征图的高，宽和通道数)

(2)池化层

池化分为最大值池化和均值池化，看别人的博客说网络中一般池化层较少，且池化操作所占用的FLOPs很少，对速度性能影响较小。我在想，

最大池化虽然没有参数，但存在计算，类似的还有Dropout等

均值池化，要求平均值，先相加再除以总数（输出特征图上一个像素点，需要浮点操作数为： k × k − 1 + 1 k \times k -1 +1 k×k−1+1。求平均值，先 k × k k \times k k×k个数相加，操作数为, k × k − 1 k\times k-1 k×k−1，然后除以 k × k k \times k k×k，浮点操作数为1），输出特征图通道数为Co，所以这里浮点操作数应该为 k ∗ k ∗ H ∗ W ∗ C o kkHWCo k∗k∗H∗W∗Co(不知道有没有问题，如有大佬知道，还望告知）

（3）全连接层

先解释一下全连接层

卷积神经网络的全连接层
在 CNN 结构中，经多个卷积层和池化层后，连接着1个或1个以上的全连接层．与 MLP 类似，全连接层中的每个神经元与其前一层的所有神经元进行全连接．全连接层可以整合卷积层或者池化层中具有类别区分性的局部信息．为了提升 CNN 网络性能，全连接层每个神经元的激励函数一般采用 ReLU 函数。最后一层全连接层的输出值被传递给一个输出，可以采用 softmax 逻辑回归（softmax regression）进行 分 类，该层也可 称为 softmax 层（softmax layer）．对于一个具体的分类任务，选择一个合适的损失函数是十分重要的，CNN 有几种常用的损失函数，各自都有不同的特点．通常，CNN 的全连接层与 MLP 结构一样，CNN 的训练算法也多采用BP算法
全连接层的每一个结点都与上一层的所有结点相连，用来把前边提取到的特征综合起来。由于其全相连的特性，一般全连接层的参数也是最多的。例如在VGG16中，第一个全连接层FC1有4096个节点，上一层POOL2是77512 = 25088个节点，则该传输需要4096*25088个权值，需要耗很大的内存

其中，x1、x2、x3为全连接层的输入，a1、a2、a3为输出，

其实现在全连接层已经基本不用了，CNN基本用FCN来代表，可用卷积层来实现全连接层的功能。设I为输入神经元个数，O为输出神经元个数，输出的每个神经元都是由输入的每个神经元乘以权重（浮点操作数为I），然后把所得的积的和相加（浮点操作数为I-1），加上一个偏差（浮点操作数为1）得到了，故FLOPs为：

FLOPs=(I+I-1) * O = (2I-1) * O(不考虑bias)

FLOPs=((I+I-1+1）* O = (2I) * O(考虑bias)

• FLOPs和参数量计算小工具

最近在github上找到了一个别人开源的在Pytorch框架中使用的FLOPs和参数量计算的小工具OpCouter，非常好用，这个工具安装也十分方便，可以直接使用pip简单的完成安装。以下放出作者开源的链接：THOP: PyTorch-OpCounter

参考链接

目标检测评价指标

机器学习算法评估指标——2D目标检测

【行人检测】miss rate versus false positives per image (FPPI) 前世今生（理论篇）