线性代数(三) | 向量组的秩 线性相关无关 几何直观理解 题解应用
文章目录
- 1 维数?向量组的秩究竟是什么?
-
- 1.1 线是一维的
- 1.2 面是二维的
- 1.3 体是三维的
- 2 线性相关、线性无关、线性表示究竟是什么?
-
- 2.1 基于以上几何直观的解题角度
- 2.2 基于方程组的解题角度
1 维数?向量组的秩究竟是什么?
1.1 线是一维的
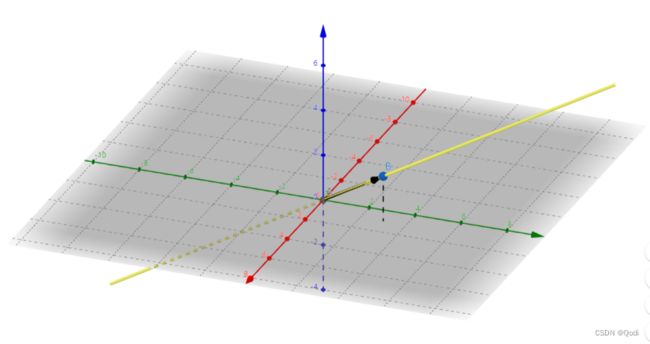
例:空间中的(1,3)这个向量(下图1黑色有向线段),从某种意义来说可以看做是一条线(黄色直线),因为这条线上的所有量,比如(2,6)(1.5,4.5)这些向量都可以用这个向量表示(其实也就是所谓的“线性表示")。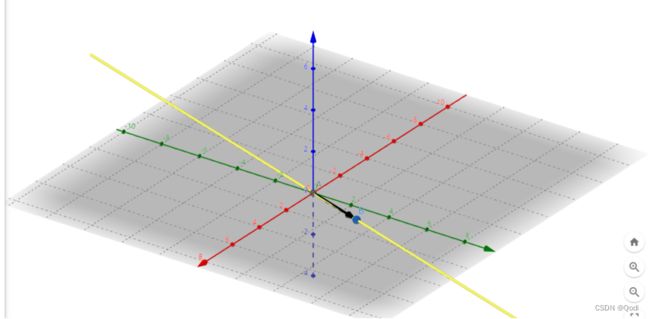
(1,3,2) 也可以看做一条线(下图1黑色有向线段)。我们可以发现,单个向量最多只能表示一维的直线(黄色直线),我们说这个向量组(单个向量也可以看为向量组)为一维的,也就意味着它的秩为1
1.2 面是二维的
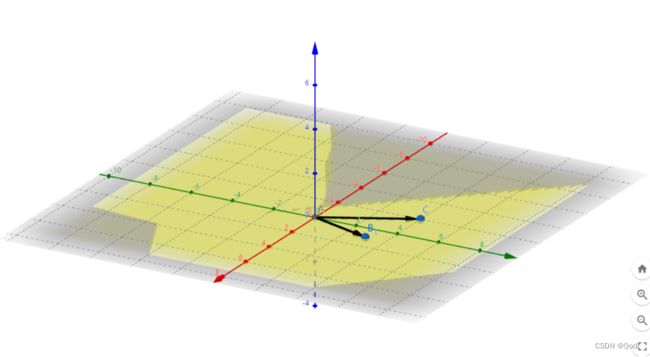
比如空间中的(1,3)和(-2,4)这两个向量可以张成一张平面,这个平面上的所有的向量都可以用这两个向量来表示,我们说这个(1,3)(2,4)这个向量组为二维的,也就是说他的秩为2
再比如空间中(1,3,2)(-2,1,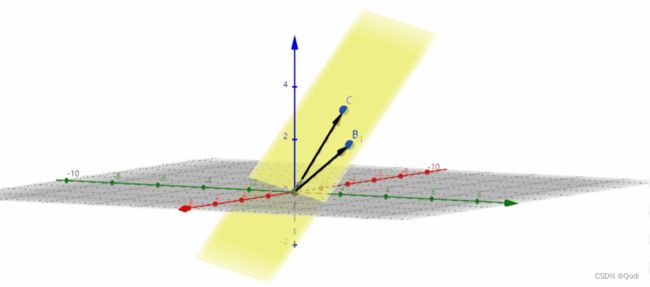
3)这两个向量可以张成一张平面,这两个向量形成的向量组为二维的
1.3 体是三维的
比如空间中(1,3,2)(-2,1,3)(1,-1,1)这三个向量可以张成一个三维的体,也就意味着,他们三个向量所组成的向量组的秩是3
2 线性相关、线性无关、线性表示究竟是什么?
那么向量组线性无关和线性相关究竟指什么呢?
我们的核心是关注这个向量组形成的一个什么样的东东
我们来看这两个A,B向量组 (单个向量也可以看为是向量组)
A:{1,2}
B:{1,2,3}
他们是表示空间中的一条线,是一维的
再看这两个向量组
A:{1,2} {3,2}
B:{1,2,3} {3,2,1}
当我们增加了一个向量时,会发现这时候这两个向量组可以张成一张平面了,是二维的了,我们也可以发现这两个向量组都是线性无关的,因为去掉某一个向量,会使得这个向量组降维,变成一维,也就是A,B向量组中每一个向量都不是多余的
我们再给这两个向量组增添一个向量
A:{1,2} {3,2} {3,1}
B:{1,2,3} {3,2,1} {1,1,1}
这时候我们会发现,A向量组依然只能张成一张平面,是二维的,表示了一个二维的平面,我们去掉其中一个向量,他都不会降维,依然是二维的,也就意味着他的秩不会改变,也就是说其中一个向量是多余的,如果存在多余向量,我们就说它是线性相关的,而这个多余的根本原因是因为其中存在一个向量可以被其他向量来线性表示。但是B向量组,我们去掉其中任意一个向量,都会使得该向量组降维,秩发生改变,如果不存在多余向量,我们就说它是线性无关的
综上我们可以如此定义线性相关和线性无关
线性无关是指,这组向量中每一个向量对于维数的增加都有贡献,去掉任何一个都会使得向量组秩改变
线性相关是指,这组向量中存在一个多余的向量(去掉这个向量以后,向量组所表示的维数不受影响)
向量组的线性表示,是指某一个向量在这个向量张成的向量空间里
注意
一个向量组所的维数,和单个向量的维数要区分。
单个向量,不管他是有几个分量,他只能表示一个一维的量
比如(1,3,5,4)这个向量组,虽然有一个四维的向量,但由于他只有一个向量,所以他只能表示一维的向量,即一条线
,也就是说它是一个一维向量组,秩为1
2.1 基于以上几何直观的解题角度
常见的一些结论就很好解释了
比如
1、任意n+1个n维向量均线性相关,n维向量最多表示n维空间,这时候如果有n+1个相应的向量,则存在多余的向量,则线性相关
2、若向量组 α 1 α 2 , . . . , α s , α s + 1 , . . . , α t \alpha_1\alpha_2,...,\alpha_s,\alpha_{s+1},...,\alpha_t α1α2,...,αs,αs+1,...,αt线性无关,则 α 1 α 2 , . . . , α s \alpha_1\alpha_2,...,\alpha_s α1α2,...,αs线性无关,条件说明这t个向量没有多余的向量,每一个向量都对于维数增加有贡献,那么它的一部分自然也没有多余的,自然也线性无关。而反过来则不正确,因为部分没有多余的,再添加的几个向量可能就会有多余的。比如(1,2,3) (2,1,3)线性无关,增加一个(2,4,6) 后就线性相关了
3、
在一些题目中的应用
2.2 基于方程组的解题角度
有一些题不适合用几何直观的,什么样的题呢,就是经过加减组合后的向量.方法是根据线性无关的定义,看看每一组合的k是否有非零解
k 1 ( α 1 − α 2 ) + k 2 ( α 2 − a 3 ) + k 3 ( α 3 − α 1 ) = 0 k_1(\alpha_1-\alpha_2)+k_2(\alpha_2-a_3)+k_3(\alpha_3-\alpha_1)=0 k1(α1−α2)+k2(α2−a3)+k3(α3−α1)=0 我们核心是要看这里的k是否只能全部为零
为了利用条件,我们打开重新组合得到 ( k 1 − k 3 ) α 1 + ( k 2 − k 1 ) α 2 + ( k 3 − k 2 ) α 3 = 0 (k_1-k_3)\alpha_1+(k_2-k_1)\alpha_2+(k_3-k_2)\alpha_3=0 (k1−k3)α1+(k2−k1)α2+(k3−k2)α3=0
由条件 我们可知 k 1 − k 3 = 0 , k 2 − k 1 = 0 , k 3 − k 2 = 0 k_1-k_3=0,k_2-k_1=0,k_3-k_2=0 k1−k3=0,k2−k1=0,k3−k2=0 所以解这个方程组就可以,当然因为这个方程组系数是等于零的,因而有非零解,所以线性相关。