神经网络遗传算法函数极值寻优
大家好,我是带我去滑雪!
对于未知的非线性函数,仅仅通过函数的输入和输出数据难以寻找函数极值,这一类问题可以通过神经网络结合遗传算法求解,利用神经网络的非线性拟合能力和遗传算法的非线性寻优能力寻找函数极值。
目录
一、问题与模型
(1)求解问题
(2)模型建立思路
二、代码实现
(1)BP神经网络训练
(3)适应度函数
(4)遗传算法主函数
一、问题与模型
(1)求解问题
利用神经网络遗传算法寻找非线性函数极值,该函数的表达式为:
![]()
函数的图像为:
通过函数图像,可以较为直观地看出函数的全局最小值为0,对应的坐标为(0,0)。虽然从函数方程和图形中很容易找出函数极值及极值对应坐标,但是在函数方程未知的情况下函数极值及对应坐标就难以找到。
(2)模型建立思路
神经网络训练拟合根据寻优函数的特点构建合适的BP神经网络,用非线性函数的输入输出数据训练BP神经网络,训练后的BP神经网络就可以预测函数输出。遗传算法极值寻优将训练后的BP神经网络预测结果作为个体适应度值,通过选择、交叉、变异操作寻找函数的全局最优值及对应输入值。
确定BP神经网络的模型结构为2-5-1,取函数的4000组输入输出数据,从中随机选择3500组数据训练神经网络,100组数据测试神经网络性能,网络训练好后用于预测非线性函数输出。
遗传算法中个体采用实数编码,由于寻优函数只有两个输入参数,所以个体长度为2。个体适应度值为BP神经网络预测值,适应度值越小,个体越优。设置交叉概率为0.4,变异概率为0.2。
二、代码实现
(1)BP神经网络训练
clc
clear
tic
load data1 input output
k=rand(1,4000);
[m,n]=sort(k);
input_train=input(n(1:3900),:)';
output_train=output(n(1:3900),:)';
input_test=input(n(3901:4000),:)';
output_test=output(n(3901:4000),:)';
[inputn,inputps]=mapminmax(input_train);
[outputn,outputps]=mapminmax(output_train);
net=newff(inputn,outputn,5);
net.trainParam.epochs=100;
net.trainParam.lr=0.1;
net.trainParam.goal=0.0000004;
net=train(net,inputn,outputn);
inputn_test=mapminmax('apply',input_test,inputps);
an=sim(net,inputn_test);
BPoutput=mapminmax('reverse',an,outputps);
figure(1)
plot(BPoutput,':og')
hold on
plot(output_test,'-*');
legend('预测输出','期望输出','fontsize',12)
title('BP网络预测输出','fontsize',12)
xlabel('样本','fontsize',12)
ylabel('输出','fontsize',12)
error=BPoutput-output_test;
figure(2)
plot(error,'-*')
title('神经网络预测误差')
figure(3)
plot((output_test-BPoutput)./BPoutput,'-*');
title('神经网络预测误差百分比')
errorsum=sum(abs(error))
toc
save data net inputps outputps输出结果:
BP神经网络预测误差百分比图:
BP神经网络预测误差图:
BP神经网络预测结果图:
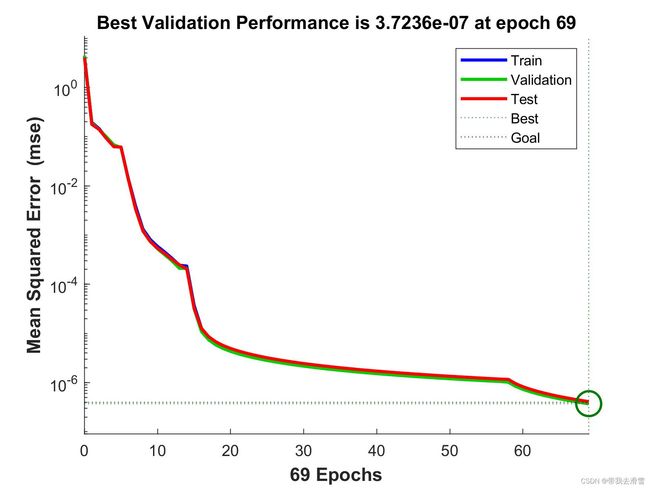
验证集均方误差迭代图:
(3)适应度函数
将训练好的BP神经网络预测输出作为个体适应度值:
function fitness = fun(x)
load data net inputps outputps
x=x';
inputn_test=mapminmax('apply',x,inputps);
an=sim(net,inputn_test);
fitness=mapminmax('reverse',an,outputps);
(4)遗传算法主函数
clc
clear
%% 初始化遗传算法参数
%初始化参数
maxgen=100; %进化代数,即迭代次数
sizepop=20; %种群规模
pcross=[0.4]; %交叉概率选择,0和1之间
pmutation=[0.2]; %变异概率选择,0和1之间
lenchrom=[1 1]; %每个变量的字串长度,如果是浮点变量,则长度都为1
bound=[-5 5;-5 5]; %数据范围
individuals=struct('fitness',zeros(1,sizepop), 'chrom',[]); %将种群信息定义为一个结构体
avgfitness=[]; %每一代种群的平均适应度
bestfitness=[]; %每一代种群的最佳适应度
bestchrom=[]; %适应度最好的染色体
%% 初始化种群计算适应度值
% 初始化种群
for i=1:sizepop
%随机产生一个种群
individuals.chrom(i,:)=Code(lenchrom,bound);
x=individuals.chrom(i,:);
%计算适应度
individuals.fitness(i)=fun(x); %染色体的适应度
end
%找最好的染色体
[bestfitness bestindex]=min(individuals.fitness);
bestchrom=individuals.chrom(bestindex,:); %最好的染色体
avgfitness=sum(individuals.fitness)/sizepop; %染色体的平均适应度
% 记录每一代进化中最好的适应度和平均适应度
trace=[avgfitness bestfitness];
%% 迭代寻优
% 进化开始
for i=1:maxgen
i
% 选择
individuals=Select(individuals,sizepop);
avgfitness=sum(individuals.fitness)/sizepop;
%交叉
individuals.chrom=Cross(pcross,lenchrom,individuals.chrom,sizepop,bound);
% 变异
individuals.chrom=Mutation(pmutation,lenchrom,individuals.chrom,sizepop,[i maxgen],bound);
% 计算适应度
for j=1:sizepop
individuals.fitness(j)=fun(x);
end
%找到最小和最大适应度的染色体及它们在种群中的位置
[newbestfitness,newbestindex]=min(individuals.fitness);
[worestfitness,worestindex]=max(individuals.fitness);
% 代替上一次进化中最好的染色体
if bestfitness>newbestfitness
bestfitness=newbestfitness;
bestchrom=individuals.chrom(newbestindex,:);
end
individuals.chrom(worestindex,:)=bestchrom;
individuals.fitness(worestindex)=bestfitness;
trace=[trace;avgfitness bestfitness]; %记录每一代进化中最好的适应度和平均适应度
end
%进化结束
%% 结果分析
[r c]=size(trace);
plot([1:r]',trace(:,2),'r-');
title('适应度曲线','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);输出结果:
优化过程中最优个体适应度值变化曲线:
遗传算法得到的最优个体适应度值为0.01,最优个体为(-0.0081,0.0014)。
更多优质内容持续发布中,请移步主页查看。
点赞+关注,下次不迷路!