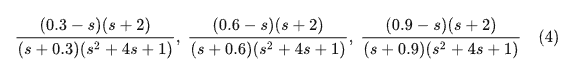最小相位、全通滤波器、群延迟、相位延迟
最小相位系统、全通滤波器、群延迟、相位延迟
这是信号处理里面最常见到的词汇,你对它们都了解吗?
(1)可利用全通滤波器进行相位均衡。
(2)可利用最小相位系统进行幅度均衡。
(3)利用这两个系统表示任意因果系统。
全通滤波器
全通滤波器,对于所有频率的正弦输入其输出幅值均不变。但,可以改变相位。所以这里的全通,就是幅值全部通过不变。
一个稳定的传递函数f((s)如果在复平面的虚轴上所有点处幅值均为1,那么这个函数就是全通函数A(s)。

A(s)的一个显著特征是其零极点关于虚轴对称。
现在,将信号sin(x)分别经过s0=0.3,0.6,0.9情形下的全通系统,得到如下响应见图1、图2。


第二个图是时域:输出信号的幅度没变吧,但位置变了(波形延迟),这就是相位滞后(相位延迟)了100°,120°,150°,就是第一个图频域(相频响应)。
总结: 在频域引起相位延迟,且对于同一频率的输入信号,不同的
A(s)输出响应的相位延迟大小不同。
最小相位系统
定义:如果一个稳定的线性时不变系统在复平面右半平面没有零点,则该系统为最小相位系统。
考虑一组不同的传递函数:

如下图,画出它们的幅频响应,相频响应。看到这些传递函数具有「相同的幅频特性曲线」,然而其相频响应曲线却各不相同。

其中,

这个传递函数在各个频率上均具有最小相移。它在复平面右半平面没有零点,因此是(具有该幅频特性的所有系统中的)最小相位系统。
事实上,所有的具有相同幅频特性曲线的传递函数G(s)均可以被表达成最小相位系统Gm(s)与全通函数A(s)级联的形式,即:
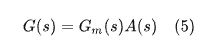
从式子上看到,全通函数A(s)不可避免地会引入相位延迟,所以G(s)的相位延迟≥Gm(s)的相位延迟,当且仅当A(s)=1,即全通函数不存在时,G(s)相位延迟最小,此时G(s)为最小相位系统。
总结:
最小相位系统的第一个特征:对同样的输入,其输出的相位延迟最小。
这里还有另一个隐含的意思,由于全通函数的存在,我们仅由系统的幅频特性曲线无法确定系统的相频特性曲线,除非已知系统是最小相位系统。
最小相位系统有什么特点呢?
除了上面的其输出的相位延迟最小,还有响应时间最小,能量延迟最小的特点。即三个“最小”。
响应时间最小:
图给出了(2)中各系统的阶跃响应曲线,可以看出,最小相位系统具有最短的响应时间。

这一点可以从最小相位系统讨论的前提进行阐述:式(2)中给出了具有相同幅特性的三个传递函数,这些函数是通过「配置右半平面的零点」得到的。
怎样方便地得到更多的具有相同幅频特性的函数呢?
另一个简单的方法是「利用延时环节」构造,见式(6)。
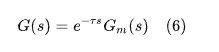
可以看到,对最小相位函数进行延时即得到非最小相位系统;上图也不难发现,通过配置右半平面零点的方式得到的非最小相位函数也有一段类似于延时的反向响应。
这两者的相似性在数学上是由如下近似关系表达的:

该式右边为一阶全通系统。
这两种(即配置右半平面零点与增加延时环节)构造非最小相位系统的方法也给我们直观理解最小相位系统响应时间最小的视角:非最小相位系统相对于最小相位系统具有滞后的特性。通俗地讲,系统比较"钝"。
能量延迟最小:
图给出了(2)中各系统的脉冲响应及对应输出的累积能量曲线(Partial Energy)。该累计能量曲线由如下定义:

其中y为脉冲响应输出。
由图可以看出,在任意时刻,最小相位系统Gm(s)的累积输出能量均不小于非最小相位系统。可以证明,最小相位系统的累积输出能量更靠近于0时刻,具有最短的能量延时。
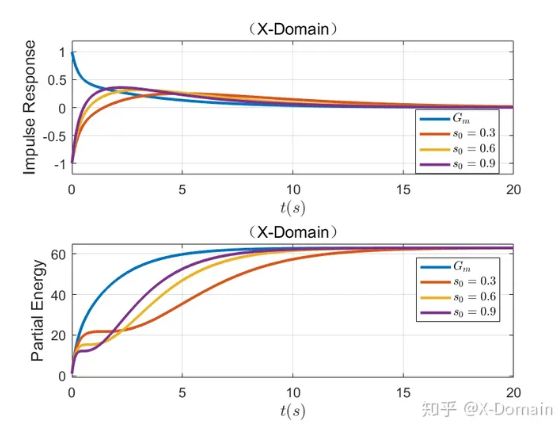
这提供了理解最小相位系统的一个新视角,即从能量角度说明了具有相同幅频特性曲线的系统中,最小相位系统为什么比非最小相位系统具有更快的响应时间。