题源:https://leetcode-cn.com/contest/weekly-contest-153/problems/maximum-subarray-sum-with-one-deletion/
给你一个整数数组,返回它的某个 非空 子数组(连续元素)在执行一次可选的删除操作后,所能得到的最大元素总和。
换句话说,你可以从原数组中选出一个子数组,并可以决定要不要从中删除一个元素(只能删一次哦),(删除后)子数组中至少应当有一个元素,然后该子数组(剩下)的元素总和是所有子数组之中最大的。
注意,删除一个元素后,子数组 不能为空。
请看示例:
示例 1:
输入:arr = [1,-2,0,3] 输出:4 解释:我们可以选出 [1, -2, 0, 3],然后删掉 -2,这样得到 [1, 0, 3],和最大。
示例 2:
输入:arr = [1,-2,-2,3] 输出:3 解释:我们直接选出 [3],这就是最大和。
示例 3:
输入:arr = [-1,-1,-1,-1]
输出:-1
解释:最后得到的子数组不能为空,所以我们不能选择 [-1] 并从中删去 -1 来得到 0。
我们应该直接选择 [-1],或者选择 [-1, -1] 再从中删去一个 -1。
提示:
1 <= arr.length <= 10^5-10^4 <= arr[i] <= 10^4
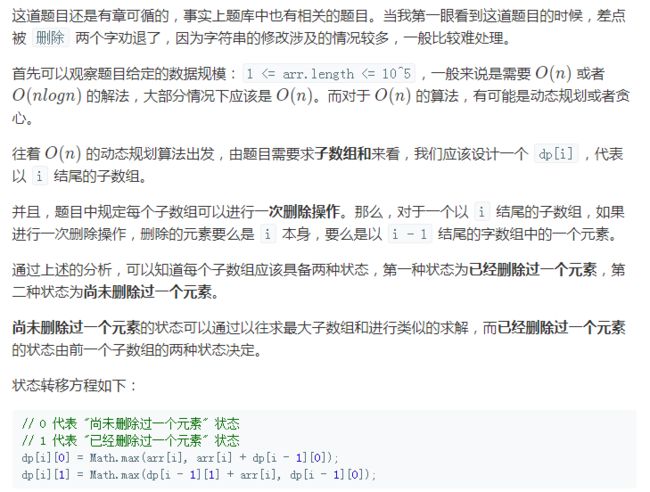
先粘代码:当然是当时没做出来的,代码是复制大佬的
主要是懒
public int maximumSum(int[] arr) { int ans = arr[0]; int len = arr.length; int[][] dp = new int[len][2]; // 初始化状态 // "尚未删除",最大子数组和为本身 dp[0][0] = arr[0]; // "已经删除",只能删除自身,最大子数组和为 0 dp[0][1] = 0; for (int i = 1; i < len; i++) { // 如果前一个子数组和大于 0,则加上 dp[i][0] = Math.max(arr[i], arr[i] + dp[i - 1][0]); // 删除的字符的两种情况: // 1. 当前数字被删除,为了满足至少一个元素,必须加上前面一个子数组 "尚未删除" 的最大值 // 2. 当前数字不被删除,则由前面子数组删除,前面子数组 "已经删除" 的最大值加上当前数字 dp[i][1] = Math.max(dp[i - 1][1] + arr[i], dp[i - 1][0]); // 两种状态都可能产生最大值 ans = Math.max(ans, dp[i][0]); ans = Math.max(ans, dp[i][1]); } return ans; } 作者:hlxing 链接:https://leetcode-cn.com/circle/article/lwbQfe/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
class Solution { public: int maximumSum(vector<int>& arr) { unsigned n = arr.size(); int dp_i_0 = -1e4, dp_i_1 = -1e4; int ans = INT_MIN; for (int i = 0; i < n; ++i) { dp_i_1 = max(dp_i_1 + arr[i], dp_i_0); dp_i_0 = max(dp_i_0 + arr[i], arr[i]); ans = max(ans, max(dp_i_0, dp_i_1)); } return ans; } }; 作者:Rui 链接:https://leetcode-cn.com/circle/discuss/OOTHdm/view/Ohytvx/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
LeetCode的网页编辑是真的服气,证明在代码编辑还差的很多
无快捷输入,无部分调试,反正各种与编译器不同,原来有人说记事本编写的
嗯,这个差不多就是个记事本
说下题解吧:算了复制大佬的,描述不清楚,dp还要深入学习下