动态规划之子序列问题（C++力扣题解）
完整版内容：
代码随想录代码随想录PDF，代码随想录百度网盘，代码随想录知识星球，代码随想录八股文PDF，代码随想录刷题路线，代码随想录知识星球八股文
https://www.programmercarl.com/0674.%E6%9C%80%E9%95%BF%E8%BF%9E%E7%BB%AD%E9%80%92%E5%A2%9E%E5%BA%8F%E5%88%97.html#_674-%E6%9C%80%E9%95%BF%E8%BF%9E%E7%BB%AD%E9%80%92%E5%A2%9E%E5%BA%8F%E5%88%97题解仅为自我回顾
目录
1：最长连续递增序列
2：最长递增子序列
3:最长重复子数组
4：最长公共子序列
5：不相交的线
6：最大子序和
7：判断子序列
8：两个字符串的删除操作
9：编辑距离（困难就这？？？）
10:回文子串
11：最长回文子序列
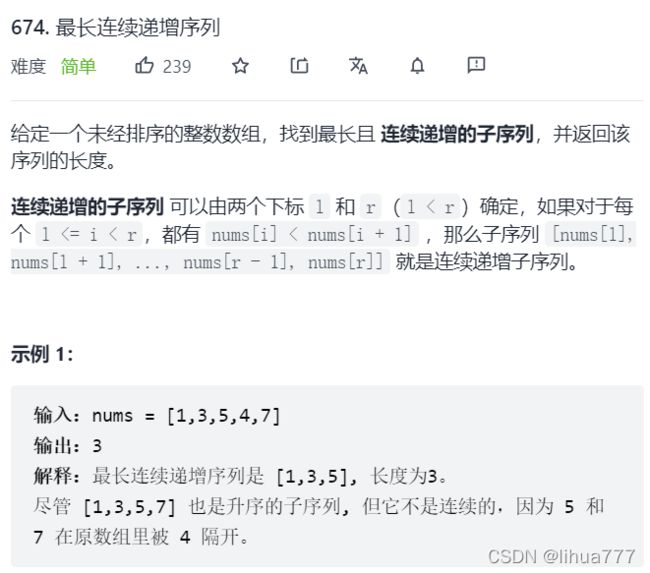
1：最长连续递增序列
动态规划思路：
（1）确定dp数组的含义：以i为结尾的最长来连续递增序列
（2）在一个数组中由于我们要求的是连续递增，所以对于相邻的两个数字有两种情况
········1：当nums[i-1]
所以递推公式为：dp[i]=dp[i-1]+1 （新的最长序列=上一个最长序列+满足条件的这个点）
·······2：当nums[i-1]>=nums[i]时，不满足题目所求，可以不用管
（3）dp数组的初始化：由于单个字符也算是一个连续递增的序列，长度为1，所以初始化dp数组为：1
（4）数组的遍历顺序：由递推公式可知，dp[i]仅由dp[i-1]推出，所以是从左向右遍历数组
（5）返回值：结合dp数组的定义可知，dp数组的最后一个数并不一定是那个最大的数，因为会存在[1,3,5,4,7]这种情况，映射到dp数组就是[1,2,3,1,2] 所以我们需要用一个变量来记录dp数组的最大值
动态规划：
class Solution {
public:
int findLengthOfLCIS(vector& nums) {
if (nums.empty()) return 0;
int result = 1;
vector dp(nums.size() ,1);
for (int i = 0; i < nums.size() - 1; i++) {
if (nums[i + 1] > nums[i]) {
dp[i + 1] = dp[i] + 1;
}
if (dp[i + 1] > result) result = dp[i + 1];
}
return result;
}
}; 解释：在dp数组的开辟大小，for循环i的其实大小，以及递推公式+1 -1的变化，调换都是可以的，小心越界问题即可
另外提一下贪心算法：（局部最优解映射到全局最优解）
class Solution {
public:
int findLengthOfLCIS(vector& nums) {
if (nums.size() == 0) return 0;
int result = 1; // 连续子序列最少也是1
int count = 1;
for (int i = 0; i < nums.size() - 1; i++) {
if (nums[i + 1] > nums[i]) {
count++;
} else { // 不连续，count从头开始
count = 1;
}
if (count > result) result = count;
}
return result;
}
}; 解释：当nums[i+1]>nums[i]时，符合条件，计数器++，否则不满足条件count重新从1开始计数
同时记录count的最大值
2：最长递增子序列
动态规划思路：
这道题与上题不同的地方在于：上题要求的是连续递增，但是本题要求的是可连续可不连续，也就是可删除和可不删除的意思，那么一次最大的区别就在于：我们不能仅仅比较两个相邻的位置，而是用i遍历数组，并且再用j遍历一遍从0到i的位置，如果发现有数字比nums[i]小，那么很显然最长递增子序列的长度要++，好了其实也就这么点改变而已
（1）dp数组的含义：i位置下，递增序列的最大长度
（2）与上题相同仍是对于数字有两种情况
·····1：当nums[j]
dp[i]=max(dp[i],dp[j]+1)
因为这个点可能不止会被用到一次，所以我们需要记录它的最大值
·····2：当nums[j]>nums[i]时，不用去管它
（3）dp数组的初始化，由定义我们可知，自己本身也算长度为1的最长递增子序列
（4）dp数组的遍历顺序：由递推公式+分析可知：dp数组由前向后退出来，所以外层用i正序遍历数组，内层用j正序遍历，i为它遍历的终点
（5）返回值：与上题同理，最后一个数字可能用不上 （当它为数组中最小的值时）
所以我们需要一个变量来记录dp数组的最大值res;
class Solution {
public:
int lengthOfLIS(vector& nums) {
if (nums.size() <= 1) return nums.size();
vector dp(nums.size(), 1);
int result = 0;
for (int i = 1; i < nums.size(); i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
}
if (dp[i] > result) result = dp[i]; // 取长的子序列
}
return result;
}
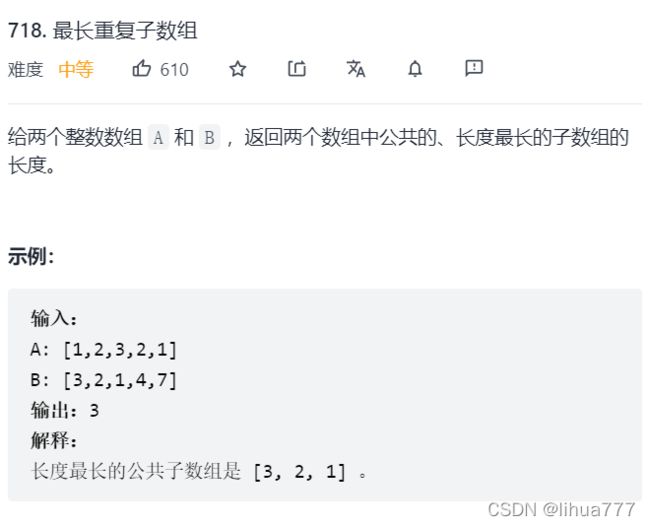
}; 3:最长重复子数组
思路解析
首先我们要明白：这是必须要求连续的情况
（1）dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]
（2）递推公式：结合定义可知,我们需要拿A,B两个字符串进行比较，那么就会产生两种情况
······1：当A[i-1]==B[j-1]时，为什么时i-1 和 j-1 ？ 注意看定义！！！
既然找到了相同的字母，那么根据定义我们应该让最长重复子数组的长度+1
所以递推公式为：dp[i][j]=dp[i-1][j-1]+1
``````2：当A[i-1]!=B[j-1]时，同理，没啥软用
（3)dp数组的初始化：当dp[0][0]时，说明两者的字符串都为空，那么公共的部分也为空：0
当dp[i][0]时，说明A字符串有东西，B字符串为空，那么同样公共的部分也为空：0
当dp[0][j]时，与上同理 均为空 所以我们只需把dp数组初始化为0即可
（4）dp数组的遍历顺序：结合定义我们发现dp[i][j]都是由dp[i-1][j-1]推出来的，所以必然时正序遍历，那么就是外层遍历A字符串，内层循环遍历B字符串，当然了，内外层交换顺序也可
（5）返回值：同理最后一个未必用到，用一个变量res去记录dp数组中的最大值
class Solution {
public:
int findLength(vector& A, vector& B) {
vector> dp (A.size() + 1, vector(B.size() + 1, 0));
int result = 0;
for (int i = 1; i <= A.size(); i++) {
for (int j = 1; j <= B.size(); j++) {
if (A[i - 1] == B[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
if (dp[i][j] > result) result = dp[i][j];
}
}
return result;
}
}; 4：最长公共子序列
思路解析：
与上题不同的是本题要求的是可删除或可不删除，其实就是和第二题差不多，只是这里换成了字符串的匹配问题
（1）dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序
（2）递推公式：与上题同理，对于字母来说，仍然是只有两种情况
······1：当text1[i-1]==text2[j-1]时：那么就把这个点+上一个最长公共子序列中
dp[i][j=dp[i-1][j-1]+1;
······2：当text1[i-1]!=text2[j-1]时：那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
（3）dp数组初始化：dp[0][0]表示两个空的字符串，公共部分为空，所以为0；
同理dp[i][0]和dp[0][j]均初始化为0
（4）遍历顺序：由递推公式可知，dp[i][j]均有前一个或其前一个的对角线推出来
所以是正序遍历，外层text1，内层text2（当然也可以相反）
（5）返回值：由于不是连续的，且其中一个字符串的末尾必须要用到，所以必然有一个dp[i][j]的填的是字符串的长度，接下来结合可删除这个性质，那么我们也可以选择放两个字符串的长度进去，反正是可删除，所以多余的末尾并不会进行计数
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
vector >dp(text1.size() + 1, vector(text2.size() + 1, 0));
for (int i = 1; i <= text1.size(); i++)
{
for (int j = 1; j <= text2.size(); j++)
{
if (text1[i - 1] == text2[j - 1])
{
dp[i][j] = max(dp[i - 1][j - 1] + 1,dp[i][j]);
}
else
{
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[text1.size()][text2.size()];
}
}; 5：不相交的线
思路解析：
直线不能相交，这就是说明在字符串A中 找到一个与字符串B相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，链接相同数字的直线就不会相交
其实就是上一题的答案………………只要相对顺序不变，其他的无关字符随便
class Solution {
public:
int maxUncrossedLines(vector& A, vector& B) {
vector> dp(A.size() + 1, vector(B.size() + 1, 0));
for (int i = 1; i <= A.size(); i++) {
for (int j = 1; j <= B.size(); j++) {
if (A[i - 1] == B[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[A.size()][B.size()];
}
}; 6：最大子序和
贪心做法：
只要前一个数>0，那么我就让它上车，如果<0，我就不让它上车，因为如果上车一个负数的值，就会导致我的数减少，那么解释的有负数是什么情况？是因为它的前一个数+它本身=3是个正数以此那么，我们就用res来记录最大值即可，因为所有的和会汇聚在一个数的身上
class Solution {
public:
int maxSubArray(vector& nums) {
int res=nums[0];//注意：因为当整个数组都是负数的时候，就很尴尬了
if(nums.size()==1) return nums[0];
for(int i=1;i0)
{
nums[i]+=nums[i-1];
}
res=max(res,nums[i]);
}
return res;
}
}; 动态规划做法：
（1）dp[i]：包括下标i之前的最大连续子序列和为dp[i]
（2）递推公式：dp[i]=max(dp[i],dp[i-1]+nums[i])
（3）dp数组初始化：当dp[0]时，包括0下拨之前的最大子序列和，即是nums[0]
（4）遍历顺序：从前向后
（5）同理：最后的不一定是最大的，因为最后面那个数万一是-很多呢，所以需要一个数去记录dp数组的最大值
class Solution {
public:
int maxSubArray(vector& nums) {
if (nums.size() == 0) return 0;
vector dp(nums.size());
dp[0] = nums[0];
int result = dp[0];
for (int i = 1; i < nums.size(); i++) {
dp[i] = max(dp[i - 1] + nums[i], nums[i]); // 状态转移公式
if (dp[i] > result) result = dp[i]; // result 保存dp[i]的最大值
}
return result;
}
}; 7：判断子序列
双指针做法：
将i指针指向s字符串，将j指针指向t字符串，如果两者相等，则让i++，每轮循环让j++,
如果i==s.length，就说明i已经走完了s字符串，即t中有i
class Solution {
public:
bool isSubsequence(string s, string t) {
int n = s.length();
int m = t.length();
int i = 0, j = 0;
while (i < n && j < m)
{
if (s[i] == t[j])
{
i++;
}
j++;
}
return i == n;
}
};动态规划做法：
（1）dp[i][j] 表示以下标i-1为结尾的字符串s和以下标j-1为结尾的字符串t，相同子序列长度
（2）状态转移方程：同样是有两种情况：字母匹配和字母不匹配
字母匹配：dp[i][j]=dp[i-1][j-1]+1
字母不匹配：dp[i][j]=dp[i][j-1]，相当于把t[j-1]这个字母删除，那么dp[i][j] 的数值就是 看s[i - 1]与 t[j - 2]的比较结果了，即：dp[i][j] = dp[i][j - 1];
（3）dp数组的初始化：dp[0][0]空即0，dp[i][0]空为0，同理
（4）遍历顺序：从前往后，s在外层，t在内层（注意：这个顺序不能改变）
（5）返回值：dp[i][j]的i位置必然是s.size()，因为用到了s的最后一位，那么对于字符串t呢，也要取最后一位，因为字母是可以删除的，你可以没有用，反正我也不计入相同子序列长度
class Solution {
public:
bool isSubsequence(string s, string t) {
vector> dp(s.size() + 1, vector(t.size() + 1, 0));
for (int i = 1; i <= s.size(); i++) {
for (int j = 1; j <= t.size(); j++) {
if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = dp[i][j - 1];
}
}
if (dp[s.size()][t.size()] == s.size()) return true;
return false;
}
}; 解释：最后看dp的最大值是否等于s字符串的长度即可
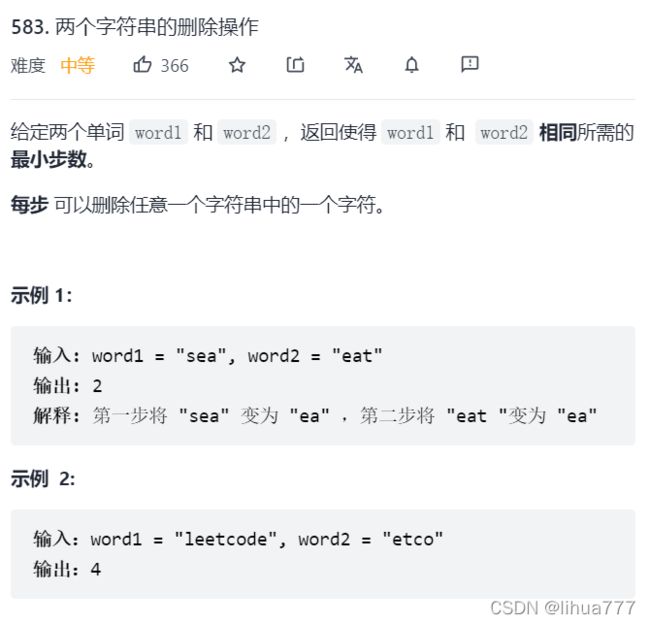
8：两个字符串的删除操作
思路解析：
(1)dp[i][j]：以i-1为结尾的字符串word1，和以j-1位结尾的字符串word2，想要达到相等，所需要删除元素的最少次数
(2)递推公式：两种可能 ： 字母相等 和字母不相等
字母相等：那么就等于上一个的情况，因为不用动= =
dp[i][j]=dp[i-1][j-1]
字母不相等：有三种情况：1.删word1的字母，2.删word2的字母，3.两个都删
情况一：删word1[i - 1]，最少操作次数为dp[i - 1][j] + 1
情况二：删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1
情况三：同时删word1[i - 1]和word2[j - 1]，操作的最少次数为dp[i - 1][j - 1] + 2
取最小值即可
(3)dp数组初始化：不讲了，倦了，0
（4）遍历顺序：不讲了，倦了，从前向后，内外层顺序可颠倒
（5）返回值：不讲了，倦了，dp两个字符串的长度
class Solution {
public:
int minDistance(string word1, string word2) {
vector> dp(word1.size() + 1, vector(word2.size() + 1));
for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
for (int i = 1; i <= word1.size(); i++) {
for (int j = 1; j <= word2.size(); j++) {
if (word1[i - 1] == word2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
}
}
}
return dp[word1.size()][word2.size()];
}
}; 9：编辑距离（困难就这？？？）
思路解析：
（1）dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离
（2）递推公式： 两种情况
当字母相等时：dp[i][j]=dp[i-1][j-1]
当字母不相等时：有三种操作：增删改
其实增可以替换为删：对一个字符串增的效果相当于另外一个字符串减
改可以替换为：同时删除最后这个字母，又同时加上这个目标字母
增：dp[i][j] = dp[i - 1][j] + 1;
删：dp[i][j] = dp[i][j - 1] + 1；
改：dp[i][j] = dp[i - 1][j - 1] + 1;
三者取最小值即可
（3）dp数组的初始化：当两个都为空时，那么操作数就是0 dp[0][0]=0;
但是当有一个不为空时：dp[i][0]=i ，将它变为空，需要有i个操作
同理dp[0][j]=j
（4）结合递推公式：从前向后，内外层随意
（5）返回：dp 两个字符串的长度
class Solution {
public:
int minDistance(string word1, string word2) {
vector> dp(word1.size() + 1, vector(word2.size() + 1, 0));
for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
for (int i = 1; i <= word1.size(); i++) {
for (int j = 1; j <= word2.size(); j++) {
if (word1[i - 1] == word2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1];
}
else {
dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}
}
}
return dp[word1.size()][word2.size()];
}
}; 10:回文子串
暴力方法：（双指针+回文串的判断）
class Solution {
public:
bool check(string s,int left,int right)
{
if(left==right) return true;
bool flag=true;
while(left=0;j--)
{
if(check(s,j,i))
{
res++;
}
}
}
return res;
}
}; 动态规划：
（1）布尔类型的dp[i][j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是dp[i][j]为true，否则为false
（2）递推公式 如果字母相等 和 字母不相等
字母不相等：false
字母相等时：
- 情况一：下标i 与 j相同，同一个字符例如a，当然是回文子串
- 情况二：下标i 与 j相差为1，例如aa，也是文子串
- 情况三：下标：i 与 j相差大于1的时候，例如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true
if (s[i] == s[j]) { if (j - i <= 1) { // 情况一 和 情况二 result++; dp[i][j] = true; } else if (dp[i + 1][j - 1]) { // 情况三 result++; dp[i][j] = true; } }（3）初始化问题：将dp数组初始化为false，就不用考虑相等的情况了
(4)遍历顺序：由递推公式dp[i+1][j-1]可知，i是从下往上得出的结果，j是从左往右得出的结果，所以从下到上遍历s，从左到右遍历s
(5)返回值，题目要求的是回文个数，所以我们已经用了dp数组来记录bool了，我们还需要一个变量来记录回文个数
class Solution {
public:
int countSubstrings(string s) {
vector> dp(s.size(), vector(s.size(), false));
int result = 0;
for (int i = s.size() - 1; i >= 0; i--) { // 注意遍历顺序
for (int j = i; j < s.size(); j++) {
if (s[i] == s[j]) {
if (j - i <= 1) { // 情况一 和 情况二
result++;
dp[i][j] = true;
} else if (dp[i + 1][j - 1]) { // 情况三
result++;
dp[i][j] = true;
}
}
}
}
return result;
}
}; 11：最长回文子序列
思路解析：回文子序列不一定要求连续
代码随想录代码随想录PDF，代码随想录百度网盘，代码随想录知识星球，代码随想录八股文PDF，代码随想录刷题路线，代码随想录知识星球八股文https://www.programmercarl.com/0516.%E6%9C%80%E9%95%BF%E5%9B%9E%E6%96%87%E5%AD%90%E5%BA%8F%E5%88%97.html#%E6%80%9D%E8%B7%AF