C++——二叉树进阶oj题

二叉树创建字符串

题目链接
思路：
二叉树递归前序遍历的变形，对于一个根，根据题意有四种情况
1、左右孩子都存在：正常前序遍历递归
2、只有左孩子没有右孩子：需要遍历左孩子，让右孩子返回空字符串。
3、只有右孩子没有左孩子：在遍历右孩子之前要在前面加上（），为的是和上面只有左孩子没有右孩子的情况区分。
4、左右孩子都不存在：均返回空字符串。
实现代码：

class Solution {
public:
    string tree2str(TreeNode* root) {
        if(root==nullptr)
        {
            return string();
        }
        string ret;
        ret+=to_string(root->val);
        if(root->left)
        {
            ret+="(";
            ret+=tree2str(root->left);
            ret+=")";
        }
        if(root->left==nullptr&&root->right!=nullptr)
        ret+="()";

        if(root->right)
        {
            ret+="(";
            ret+=tree2str(root->right);
            ret+=")";
        }
        return ret;

    }
};

二叉树的分层遍历1

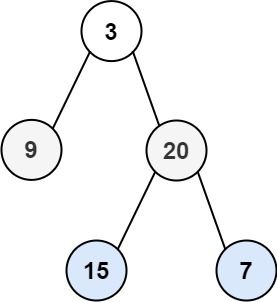
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

题目链接
思路：
利用一个队列控制层序遍历的结点，因为题中要求返回vector>，所以层序遍历的同时要记录当前走到第几层了，第一层和第二层的元素不能放在同一个vector中。
定义一个queue q，先从根节点开始，将地址push到q中，设置一个T_level变量来标识层数，一开始设置为1，表示在二叉树的第一层，然后在q中每pop一个结点就让T_level-1，pop的同时如果左右孩子都不为空，那么把它的左右孩子也push，当T_level==0的时候，此时队列里就剩下下一层的元素了，把queue的size赋值给T_level，然后将刚才的vector尾插到vector>中，再开始下一层的遍历。
实现代码：

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> vv;
        if(root==nullptr)
        {
            return vv;
        }
        
        queue<TreeNode*> q;

        int T_level=1;
        q.push(root);

        while(!q.empty())
        {
            vector<int> tmp;

            while(T_level--)
            {
                tmp.push_back(q.front()->val);
                
                
                if(q.front()->left)
                {
                    q.push(q.front()->left);
                }
                if(q.front()->right)
                {
                    q.push(q.front()->right);
                }

                q.pop();
                
            }
            T_level=q.size();
            vv.push_back(tmp);
        }
        return vv;
    }
};

二叉树的分层遍历2

题目链接
思路：
将上一题的vector>逆置一下即可。
实现代码：

class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
        vector<vector<int>> vv;
        if(root==nullptr)
        {
            return vv;
        }
        
        queue<TreeNode*> q;

        int T_level=1;
        q.push(root);

        while(!q.empty())
        {
            vector<int> tmp;

            while(T_level--)
            {
                tmp.push_back(q.front()->val);
                
                
                if(q.front()->left)
                {
                    q.push(q.front()->left);
                }
                if(q.front()->right)
                {
                    q.push(q.front()->right);
                }

                q.pop();
                
            }
            T_level=q.size();
            vv.push_back(tmp);
        }
        reverse(vv.begin(),vv.end());

        return vv;
    }
};

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先

题目链接
思路：
写一个Get_Path函数把到两个结点的路径用两个stack记录下来，然后让路径长的出栈，直到两个结点的路径长度相同，此时从两个栈的栈顶开始比对看是否有相同的结点，一旦发现相同的结点，这个结点就是要找的最近公共祖先。
实现代码：

class Solution {
public:
    bool Get_Path(TreeNode* &root, TreeNode* & FindNode,stack<TreeNode*>& path)//
    {
        if(root==nullptr)
        {
            return false;
        }

        path.push(root);


        if(root==FindNode)
        return true;
        
        if(Get_Path(root->left,FindNode,path))
        {
            return true;
        }

        if(Get_Path(root->right,FindNode,path))
        {
            return true;
        }

        //以root的左右孩子为起点没有找到FindNode
        path.pop();
        return false;
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        
        stack<TreeNode*> pPath;
        stack<TreeNode*> qPath;

        Get_Path(root,p,pPath);
        Get_Path(root,q,qPath);
        
		//两个栈倒着找
        while(pPath.size()!=qPath.size())
        {
            if(pPath.size()>qPath.size())
            {
                pPath.pop();
            }
            else
            {
                qPath.pop();
            }
        }
        while(pPath.top()!=qPath.top())
        {
            pPath.pop();
            qPath.pop();
        }

        return pPath.top();
    }
};

二叉树搜索树转换成排序双向链表。

题目链接
思路：
最简单的一种思路：用vector把二叉搜索树遍历的序列存起来，然后遍历vector，按双向链表的方式把它们链接起来即可。
递归的思路：另外写一个InorderConvert函数，中序遍历递归构建双向链表，这里设计函数的时候prev变量要加引用，cur表示当前结点。
实现代码：

class Solution {
public:
	void InorderConvert(TreeNode*cur,TreeNode*&prev)
	{
		if(cur==nullptr)
		{
			return;
		}

		InorderConvert(cur->left, prev);
		//画图才能较好的理解
		cur->left=prev;
		if(prev)
		prev->right=cur;
		prev=cur;

		InorderConvert(cur->right,prev);
	}

    TreeNode* Convert(TreeNode* pRootOfTree) {
        
		TreeNode*prev=nullptr;
		InorderConvert(pRootOfTree,prev);
		
		//前面已经链接好了，后面找双向链表的头，然后返回即可
		TreeNode* head = pRootOfTree;
		while(head&&head->left)
		{
			head = head->left;
		}

		return head;
    }
};

根据一棵树的中序遍历与后序遍历构造二叉树

题目链接

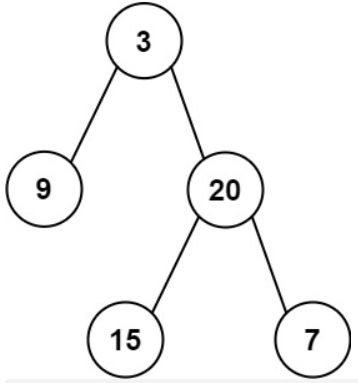
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

思路：
模拟建树的过程：
在后序遍历postorder中从后往前，可以依次确定一棵树的根在哪，确定根之后，
在中序遍历inorder中找到在后序遍历postorder中确定的根的下标N，
在中序遍历序列里再划分左右子树区间：[0，N-1]N[N+1，inorder.size()-1]
上面的例子中很显然第一次N==1
[0，0]是左子树区间，[2，4]是右子树区间
但是观察发现postorder的“根”从后往前，都是先右后左的，那么在确定根之后首先应该建立右子树，然后建立左子树。如果不这样的话，先建立左子树的话，结合上一步确定的左子树区间[0，0]以及postorder中下一次建树的根20，[0，0]中根本就找不到创建左子树的根20，那么就出错了。
然后根据在左右区间找到的根然后再建树，再递归。
实现代码：

//代码说起来容易写起来难！
class Solution {
public:
    TreeNode*_buildTree(vector<int>& inorder, vector<int>& postorder,
    int &posti,int inbegin,int inend)
	//posti是标记当前的走到postorder的什么位置了，
	//一定要加引用，因为左子树/右子树每创建一个结点
	//都必须消耗postorder的一个节点。
    //inbegin和inend分别是左右区间
    {
        if(inbegin>inend)
        {
            return nullptr;
        }

        TreeNode*root=new TreeNode(postorder[posti]);//先建树
		
		//在inorder中根据postorder找根所在的位置，
		//根据这个根的位置才能划分左右区间
		
        int root_in_inorder=inbegin;
        while(inorder[root_in_inorder]!=postorder[posti])
        //当有一个结点的时候，提前posti--会导致越界
        {
            root_in_inorder++;
        }
        
        //上面工作都做好了，posti--
        posti--;
        
        root->right=_buildTree(inorder,postorder,posti,root_in_inorder+1,inend);

        root->left=_buildTree(inorder,postorder,posti,inbegin,root_in_inorder-1);

        return root;
    }
    

    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        int postend=postorder.size()-1;//后序遍历的最后一个元素的下标
		
        return _buildTree(inorder,postorder,postend,0,inorder.size()-1);
    }
};

根据一棵树的前序遍历与中序遍历构造二叉树

题目链接
思路：
与前一题类似但也有不同之处。
根据前序遍历从前往后确定根，然后根据中序遍历确定左右区间，前序的话那就应该先建右子树，在建左子树，然后注意prei也就是记录前序遍历的坐标，一定要加引用，因为左子树/右子树每创建一个结点，都必须消耗postorder的一个节点。
实现代码：

class Solution {
public:
    TreeNode* _buildTree(vector<int> & preorder,vector<int> &inorder,
        int & prei,int inbegin,int inend)
    {
        if(inbegin>inend)
        {
            return nullptr;
        }
		
		//在inorder中根据preorder找根所在的位置，
		//根据这个根的位置才能划分左右区间
        int rooti=inbegin;
        while(rooti<=inend)
        {
            if(inorder[rooti]==preorder[prei])
            break;

            ++rooti;
        }

        TreeNode *root=new TreeNode(preorder[prei]);
        prei++;
        
        root->left=_buildTree(preorder,inorder,prei,inbegin,rooti-1);
        root->right=_buildTree(preorder,inorder,prei,rooti+1,inend);
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int pi=0;//从前序遍历的第一个元素开始确定根的位置
        return _buildTree(preorder,inorder,pi,0,inorder.size()-1);
    }
};