STM32F407-Discovery的硬件FPU
本文基于STM32 HAL 库版本:STM32Cube_FW_F4_V1.27.0
1. STM32F407的FPU简介
FPU:Float Point Unit,也就是浮点运算单元。如果是定点 CPU(没有 FPU 的 CPU)计算浮点数,则按照 IEEE-754 标准,完成运算需要大量的指令,很耗费时间,几乎不能满足实时性的要求。但是对于有 FPU 的芯片来说,完成一个浮点运算或许只是几条指令就可以搞定,速度相对就快很多。
STM32F4具有有 32 位单精度硬件FPU[能加速计算float类型的数据],支持浮点指令集,相对于Cortex M0 和 Cortex M3高出数十倍甚至上百倍的运算性能。
STM32F4通过配置协处理器控制寄存器(CPACR)就可以决定是否使用FPU,如果使用了FPU,遇到浮点运算,则自动开启硬件加速。
该寄存器描述如下图:
只需要把bit 20/21/22/23都配成1,即可开启FPU硬件加速。
2. 配置
文件:system_stm32f4xx.c,是否开启FPU由两个宏定义来进行管理:
__FPU_PRESENT:这个宏是指当前的IC是否具有FPU
__FPU_USED:是否开启FPU
__FPU_PRESENT在对应头文件中就有定义,这里是:stm32f407xx.h
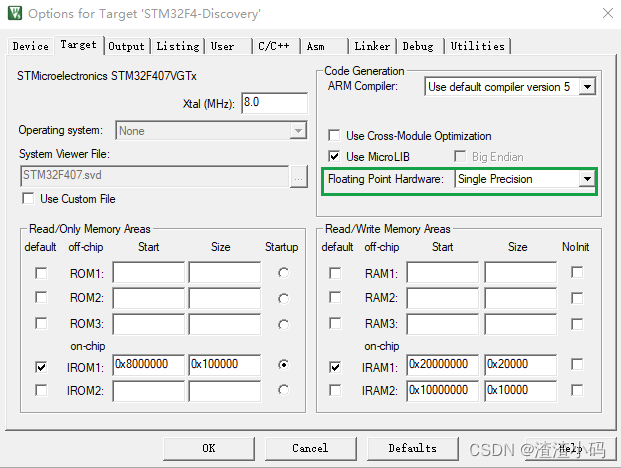
是否开启取决于应用场景,只需要在MDK中配置即可:
Floating Point Hardware:选择Single Precision则自动关联到宏__FPU_USED且将其值置为1;如果选择Not Used,则宏__FPU_USED的值为0。
3. 对比测试
实例:运算128个点的复数fft,使用GPIO输出高低电平测量算法运行时长。
用户src目录下新增两个文件:complex.c和fft.c
complex.c:
#include "complex.h"
void complex_add(complex a, complex b, complex *c)
{
c->real = a.real + b.real;
c->img = a.img + b.img;
}
void complex_sub(complex a, complex b, complex *c)
{
c->real = a.real - b.real;
c->img = a.img - b.img;
}
void complex_mul(complex a, complex b, complex *c)
{
c->real = a.real*b.real - a.img*b.img;
c->img = a.real*b.img + a.img*b.real;
}
void complex_div(complex a, complex b, complex*c)
{
c->real = (a.real*b.real + a.img*b.img)/(b.real*b.real + b.img*b.img);
c->img = (a.img*b.real - a.real*b.img)/(b.real*b.real + b.img*b.img);
}
fft.c:
#include
#include
#include "fft.h"
#include "complex.h"
complex Wn, Temp, Res;
int L, B, P, K;
//输入序列的长度必须是2的整数次幂
void Reader_Sort(complex *x, int len)
{
complex temp;
int cur_rev = 0; //从0开始,递推出所有原自然排序数对应的倒序数
int k = len / 2; //初始化权值系数
int i, j;
for (j = 1; j <= len - 1; j++) {
//当前倒序数的最高位为0,
if (cur_rev < k) {
//把temp的最高位从0变为1(加上权系数)即可得到下一个倒序数
cur_rev = cur_rev + k;
} else {
//当前倒序数的最高位为1
while (cur_rev >= k) {
//把最高位从1变为0(减去权系数即可)
cur_rev = cur_rev - k;
//没跳出循环就说明次高位为1,则更新权系数,将当前位设为0,......
k = k / 2;
}
//当前位(最高位)为0,跳出while(),置为1(加上权系数),即得当前倒序数
cur_rev = cur_rev + k;
//还原权系数值
k = len / 2;
}
//printf("j=%d, cur_rev=%d\n", j, cur_rev);
//互换x[j]和x[cur_rev]
if (j < cur_rev) {
//实数部分互换
temp.real = x[j].real;
x[j].real = x[cur_rev].real;
x[cur_rev].real = temp.real;
//虚数部分互换
temp.img = x[j].img;
x[j].img = x[cur_rev].img;
x[cur_rev].img = temp.img;
}
}
}
void FFT(complex *input_seq, int SEQ_N, int SEQ_M, complex res_seq[])
{
int i, j, r;
int L, B, K, P;
complex Temp, Wn, Res;
if (!input_seq) {
printf("input sequence can be NULL\n");
return ;
}
Reader_Sort(input_seq, SEQ_N);
for (L=1; L <= SEQ_M; L++) {
B=1;
B=(int)pow(2, L-1);
for (j=0; j<=B-1; j++) {
K=(int)pow(2, SEQ_M-L);
P=1;
P=K*j;
for (i=0; i<=K-1; i++) {
r=j;
r=j+2*B*i;
Temp = input_seq[r];
Wn.real = cos((2*PI)/SEQ_N*P);
Wn.img = -1*sin((2*PI)/SEQ_N*P);
complex_mul(input_seq[r+B], Wn, &Res);
input_seq[r].real=input_seq[r].real + Res.real;
input_seq[r].img=input_seq[r].img + Res.img;
input_seq[r+B].real=Temp.real - Res.real;
input_seq[r+B].img=Temp.img - Res.img;
}
}
}
if (!res_seq) {
printf("result sequence is NULL\n");
return ;
} else {
for(i=0; i 对应地用户目录inc下新增文件complex.h和fft.h
complex.h:
#ifndef __COMPLEX_H_
#define __COMPLEX_H_
typedef struct {
float real;
float img;
} complex;
void complex_add(complex a, complex b, complex *c);
void complex_sub(complex a, complex b, complex *c);
void complex_mul(complex a, complex b, complex *c);
void complex_div(complex a, complex b, complex*c);
#endif
fft.h:
#ifndef _FFT_H_
#define _FFT_H_
#include "complex.h"
#define PI (3.14159267)
/*
参数:
(1)N=2^M
(2)L=1~M,第L级
(3)旋转因子的指数p,k是p的增量,p=p*k
(4)B是 元素抽取间隔 = 运算的种类(旋转因子的种类)
*/
#define N (128)
#define M (log(N)/log(2))
void FFT(complex *input_seq, int SEQ_N, int SEQ_M, complex res_seq[]);
void iFFT(complex *input_seq, int SEQ_N, int SEQ_M, complex res_seq[]);
#endif
main.h中添加头文件
main.c:
/* Includes ------------------------------------------------------------------*/
#include "main.h"
int fft_test(void)
{
int i;
complex INPUT_SEQ[N], RES_SEQ[N], OUTPUT_SEQ[N];
float SEQ_DAT[N], dataR[N], dataI[N];
//构造实数序列
for (i=0; i < N; i++) {
SEQ_DAT[i]=i+0.0;
}
//构造虚数序列
for (i=0; i配置使用FPU,则128个点的正反变换用时大概是0.7ms。
测量结果:
如果不用FPU(可以直接屏蔽这行代码进行测试):则用时0.2s左右。
测量结果:
串口打印:逆变换后的数据
[09:42:26.534] ifft: OUTPUT_SEQ[1].real=1.000000, OUTPUT_SEQ[1].img=0.000000
[09:42:26.598] ifft: OUTPUT_SEQ[2].real=2.000000, OUTPUT_SEQ[2].img=0.000000
[09:42:26.663] ifft: OUTPUT_SEQ[3].real=3.000000, OUTPUT_SEQ[3].img=0.000000
[09:42:26.726] ifft: OUTPUT_SEQ[4].real=4.000000, OUTPUT_SEQ[4].img=0.000000
[09:42:26.790] ifft: OUTPUT_SEQ[5].real=5.000000, OUTPUT_SEQ[5].img=0.000000
[09:42:26.854] ifft: OUTPUT_SEQ[6].real=6.000000, OUTPUT_SEQ[6].img=0.000000
[09:42:26.918] ifft: OUTPUT_SEQ[7].real=7.000000, OUTPUT_SEQ[7].img=0.000000
[09:42:26.982] ifft: OUTPUT_SEQ[8].real=8.000000, OUTPUT_SEQ[8].img=0.000000
[09:42:27.046] ifft: OUTPUT_SEQ[9].real=9.000000, OUTPUT_SEQ[9].img=0.000000
[09:42:27.110] ifft: OUTPUT_SEQ[10].real=10.000000, OUTPUT_SEQ[10].img=0.000000
[09:42:27.174] ifft: OUTPUT_SEQ[11].real=11.000000, OUTPUT_SEQ[11].img=0.000000
[09:42:27.254] ifft: OUTPUT_SEQ[12].real=12.000000, OUTPUT_SEQ[12].img=0.000000
[09:42:27.317] ifft: OUTPUT_SEQ[13].real=13.000000, OUTPUT_SEQ[13].img=0.000000
[09:42:27.381] ifft: OUTPUT_SEQ[14].real=14.000000, OUTPUT_SEQ[14].img=0.000000
[09:42:27.445] ifft: OUTPUT_SEQ[15].real=15.000000, OUTPUT_SEQ[15].img=0.000000
[09:42:27.525] ifft: OUTPUT_SEQ[16].real=16.000000, OUTPUT_SEQ[16].img=0.000000
[09:42:27.589] ifft: OUTPUT_SEQ[17].real=17.000000, OUTPUT_SEQ[17].img=0.000000
[09:42:27.653] ifft: OUTPUT_SEQ[18].real=18.000000, OUTPUT_SEQ[18].img=0.000000
[09:42:27.717] ifft: OUTPUT_SEQ[19].real=19.000000, OUTPUT_SEQ[19].img=0.000000
[09:42:27.780] ifft: OUTPUT_SEQ[20].real=20.000000, OUTPUT_SEQ[20].img=0.000000
[09:42:27.860] ifft: OUTPUT_SEQ[21].real=21.000000, OUTPUT_SEQ[21].img=0.000000
[09:42:27.924] ifft: OUTPUT_SEQ[22].real=22.000000, OUTPUT_SEQ[22].img=0.000000
[09:42:27.988] ifft: OUTPUT_SEQ[23].real=23.000000, OUTPUT_SEQ[23].img=0.000000
[09:42:28.052] ifft: OUTPUT_SEQ[24].real=24.000000, OUTPUT_SEQ[24].img=0.000000
[09:42:28.132] ifft: OUTPUT_SEQ[25].real=25.000000, OUTPUT_SEQ[25].img=0.000000
[09:42:28.196] ifft: OUTPUT_SEQ[26].real=26.000000, OUTPUT_SEQ[26].img=0.000000
[09:42:28.260] ifft: OUTPUT_SEQ[27].real=27.000000, OUTPUT_SEQ[27].img=0.000000
[09:42:28.324] ifft: OUTPUT_SEQ[28].real=28.000000, OUTPUT_SEQ[28].img=0.000000
[09:42:28.404] ifft: OUTPUT_SEQ[29].real=29.000000, OUTPUT_SEQ[29].img=0.000000
[09:42:28.468] ifft: OUTPUT_SEQ[30].real=30.000000, OUTPUT_SEQ[30].img=0.000000
[09:42:28.532] ifft: OUTPUT_SEQ[31].real=31.000000, OUTPUT_SEQ[31].img=0.000000
[09:42:28.596] ifft: OUTPUT_SEQ[32].real=32.000000, OUTPUT_SEQ[32].img=0.000000
[09:42:28.676] ifft: OUTPUT_SEQ[33].real=33.000000, OUTPUT_SEQ[33].img=0.000000
[09:42:28.740] ifft: OUTPUT_SEQ[34].real=34.000000, OUTPUT_SEQ[34].img=0.000000
[09:42:28.803] ifft: OUTPUT_SEQ[35].real=35.000000, OUTPUT_SEQ[35].img=0.000000
[09:42:28.868] ifft: OUTPUT_SEQ[36].real=36.000000, OUTPUT_SEQ[36].img=0.000000
[09:42:28.947] ifft: OUTPUT_SEQ[37].real=37.000000, OUTPUT_SEQ[37].img=0.000000
[09:42:29.011] ifft: OUTPUT_SEQ[38].real=38.000000, OUTPUT_SEQ[38].img=0.000000
[09:42:29.075] ifft: OUTPUT_SEQ[39].real=39.000000, OUTPUT_SEQ[39].img=0.000000
[09:42:29.139] ifft: OUTPUT_SEQ[40].real=40.000000, OUTPUT_SEQ[40].img=0.000000
[09:42:29.203] ifft: OUTPUT_SEQ[41].real=41.000000, OUTPUT_SEQ[41].img=0.000000
[09:42:29.282] ifft: OUTPUT_SEQ[42].real=42.000000, OUTPUT_SEQ[42].img=0.000000
[09:42:29.346] ifft: OUTPUT_SEQ[43].real=43.000000, OUTPUT_SEQ[43].img=0.000000
[09:42:29.410] ifft: OUTPUT_SEQ[44].real=44.000000, OUTPUT_SEQ[44].img=0.000000
[09:42:29.474] ifft: OUTPUT_SEQ[45].real=45.000000, OUTPUT_SEQ[45].img=0.000000
[09:42:29.554] ifft: OUTPUT_SEQ[46].real=46.000000, OUTPUT_SEQ[46].img=0.000000
[09:42:29.618] ifft: OUTPUT_SEQ[47].real=47.000000, OUTPUT_SEQ[47].img=0.000000
[09:42:29.682] ifft: OUTPUT_SEQ[48].real=48.000000, OUTPUT_SEQ[48].img=0.000000
[09:42:29.746] ifft: OUTPUT_SEQ[49].real=49.000000, OUTPUT_SEQ[49].img=0.000000
[09:42:29.827] ifft: OUTPUT_SEQ[50].real=50.000000, OUTPUT_SEQ[50].img=0.000000
[09:42:29.890] ifft: OUTPUT_SEQ[51].real=51.000000, OUTPUT_SEQ[51].img=0.000000
[09:42:29.954] ifft: OUTPUT_SEQ[52].real=52.000000, OUTPUT_SEQ[52].img=0.000000
[09:42:30.018] ifft: OUTPUT_SEQ[53].real=53.000000, OUTPUT_SEQ[53].img=0.000000
[09:42:30.098] ifft: OUTPUT_SEQ[54].real=54.000000, OUTPUT_SEQ[54].img=0.000000
[09:42:30.162] ifft: OUTPUT_SEQ[55].real=55.000000, OUTPUT_SEQ[55].img=0.000000
[09:42:30.226] ifft: OUTPUT_SEQ[56].real=56.000000, OUTPUT_SEQ[56].img=0.000000
[09:42:30.290] ifft: OUTPUT_SEQ[57].real=57.000000, OUTPUT_SEQ[57].img=0.000000
[09:42:30.354] ifft: OUTPUT_SEQ[58].real=58.000000, OUTPUT_SEQ[58].img=0.000000
[09:42:30.433] ifft: OUTPUT_SEQ[59].real=59.000000, OUTPUT_SEQ[59].img=0.000000
[09:42:30.497] ifft: OUTPUT_SEQ[60].real=60.000000, OUTPUT_SEQ[60].img=0.000000
[09:42:30.561] ifft: OUTPUT_SEQ[61].real=61.000000, OUTPUT_SEQ[61].img=0.000000
[09:42:30.625] ifft: OUTPUT_SEQ[62].real=62.000000, OUTPUT_SEQ[62].img=0.000000
[09:42:30.705] ifft: OUTPUT_SEQ[63].real=63.000000, OUTPUT_SEQ[63].img=0.000000
[09:42:30.769] ifft: OUTPUT_SEQ[64].real=64.000000, OUTPUT_SEQ[64].img=0.000000
[09:42:30.833] ifft: OUTPUT_SEQ[65].real=65.000000, OUTPUT_SEQ[65].img=0.000000
[09:42:30.897] ifft: OUTPUT_SEQ[66].real=66.000000, OUTPUT_SEQ[66].img=0.000000
[09:42:30.977] ifft: OUTPUT_SEQ[67].real=67.000000, OUTPUT_SEQ[67].img=0.000000
[09:42:31.040] ifft: OUTPUT_SEQ[68].real=68.000000, OUTPUT_SEQ[68].img=0.000000
[09:42:31.104] ifft: OUTPUT_SEQ[69].real=69.000000, OUTPUT_SEQ[69].img=0.000000
[09:42:31.168] ifft: OUTPUT_SEQ[70].real=70.000000, OUTPUT_SEQ[70].img=0.000000
[09:42:31.248] ifft: OUTPUT_SEQ[71].real=71.000000, OUTPUT_SEQ[71].img=0.000000
[09:42:31.312] ifft: OUTPUT_SEQ[72].real=72.000000, OUTPUT_SEQ[72].img=0.000000
[09:42:31.376] ifft: OUTPUT_SEQ[73].real=73.000000, OUTPUT_SEQ[73].img=0.000000
[09:42:31.440] ifft: OUTPUT_SEQ[74].real=74.000000, OUTPUT_SEQ[74].img=0.000000
[09:42:31.520] ifft: OUTPUT_SEQ[75].real=75.000000, OUTPUT_SEQ[75].img=0.000000
[09:42:31.584] ifft: OUTPUT_SEQ[76].real=76.000000, OUTPUT_SEQ[76].img=0.000000
[09:42:31.647] ifft: OUTPUT_SEQ[77].real=77.000000, OUTPUT_SEQ[77].img=0.000000
[09:42:31.711] ifft: OUTPUT_SEQ[78].real=78.000000, OUTPUT_SEQ[78].img=0.000000
[09:42:31.775] ifft: OUTPUT_SEQ[79].real=79.000000, OUTPUT_SEQ[79].img=0.000000
[09:42:31.856] ifft: OUTPUT_SEQ[80].real=80.000000, OUTPUT_SEQ[80].img=0.000000
[09:42:31.919] ifft: OUTPUT_SEQ[81].real=81.000000, OUTPUT_SEQ[81].img=0.000000
[09:42:31.984] ifft: OUTPUT_SEQ[82].real=82.000000, OUTPUT_SEQ[82].img=0.000000
[09:42:32.048] ifft: OUTPUT_SEQ[83].real=83.000000, OUTPUT_SEQ[83].img=0.000000
[09:42:32.128] ifft: OUTPUT_SEQ[84].real=84.000000, OUTPUT_SEQ[84].img=0.000000
[09:42:32.192] ifft: OUTPUT_SEQ[85].real=85.000000, OUTPUT_SEQ[85].img=0.000000
[09:42:32.255] ifft: OUTPUT_SEQ[86].real=86.000000, OUTPUT_SEQ[86].img=0.000000
[09:42:32.319] ifft: OUTPUT_SEQ[87].real=87.000000, OUTPUT_SEQ[87].img=0.000000
[09:42:32.399] ifft: OUTPUT_SEQ[88].real=88.000000, OUTPUT_SEQ[88].img=0.000000
[09:42:32.463] ifft: OUTPUT_SEQ[89].real=89.000000, OUTPUT_SEQ[89].img=0.000000
[09:42:32.527] ifft: OUTPUT_SEQ[90].real=90.000000, OUTPUT_SEQ[90].img=0.000000
[09:42:32.591] ifft: OUTPUT_SEQ[91].real=91.000000, OUTPUT_SEQ[91].img=0.000000
[09:42:32.671] ifft: OUTPUT_SEQ[92].real=92.000000, OUTPUT_SEQ[92].img=0.000000
[09:42:32.735] ifft: OUTPUT_SEQ[93].real=93.000000, OUTPUT_SEQ[93].img=0.000000
[09:42:32.799] ifft: OUTPUT_SEQ[94].real=94.000000, OUTPUT_SEQ[94].img=0.000000
[09:42:32.862] ifft: OUTPUT_SEQ[95].real=95.000000, OUTPUT_SEQ[95].img=0.000000
[09:42:32.926] ifft: OUTPUT_SEQ[96].real=96.000000, OUTPUT_SEQ[96].img=0.000000
[09:42:33.006] ifft: OUTPUT_SEQ[97].real=97.000000, OUTPUT_SEQ[97].img=0.000000
[09:42:33.070] ifft: OUTPUT_SEQ[98].real=98.000000, OUTPUT_SEQ[98].img=0.000000
[09:42:33.134] ifft: OUTPUT_SEQ[99].real=99.000000, OUTPUT_SEQ[99].img=0.000000
[09:42:33.198] ifft: OUTPUT_SEQ[100].real=100.000000, OUTPUT_SEQ[100].img=0.000000
[09:42:33.278] ifft: OUTPUT_SEQ[101].real=101.000000, OUTPUT_SEQ[101].img=0.000000
[09:42:33.341] ifft: OUTPUT_SEQ[102].real=102.000000, OUTPUT_SEQ[102].img=0.000000
[09:42:33.421] ifft: OUTPUT_SEQ[103].real=103.000000, OUTPUT_SEQ[103].img=0.000000
[09:42:33.485] ifft: OUTPUT_SEQ[104].real=104.000000, OUTPUT_SEQ[104].img=0.000000
[09:42:33.565] ifft: OUTPUT_SEQ[105].real=105.000000, OUTPUT_SEQ[105].img=0.000000
[09:42:33.629] ifft: OUTPUT_SEQ[106].real=106.000000, OUTPUT_SEQ[106].img=0.000000
[09:42:33.693] ifft: OUTPUT_SEQ[107].real=107.000000, OUTPUT_SEQ[107].img=0.000000
[09:42:33.773] ifft: OUTPUT_SEQ[108].real=108.000000, OUTPUT_SEQ[108].img=0.000000
[09:42:33.836] ifft: OUTPUT_SEQ[109].real=109.000000, OUTPUT_SEQ[109].img=0.000000
[09:42:33.917] ifft: OUTPUT_SEQ[110].real=110.000000, OUTPUT_SEQ[110].img=0.000000
[09:42:33.981] ifft: OUTPUT_SEQ[111].real=111.000000, OUTPUT_SEQ[111].img=0.000000
[09:42:34.061] ifft: OUTPUT_SEQ[112].real=112.000000, OUTPUT_SEQ[112].img=0.000000
[09:42:34.125] ifft: OUTPUT_SEQ[113].real=113.000000, OUTPUT_SEQ[113].img=0.000000
[09:42:34.189] ifft: OUTPUT_SEQ[114].real=114.000000, OUTPUT_SEQ[114].img=0.000000
[09:42:34.269] ifft: OUTPUT_SEQ[115].real=115.000000, OUTPUT_SEQ[115].img=0.000000
[09:42:34.333] ifft: OUTPUT_SEQ[116].real=116.000000, OUTPUT_SEQ[116].img=0.000000
[09:42:34.413] ifft: OUTPUT_SEQ[117].real=117.000000, OUTPUT_SEQ[117].img=0.000000
[09:42:34.476] ifft: OUTPUT_SEQ[118].real=118.000000, OUTPUT_SEQ[118].img=0.000000
[09:42:34.556] ifft: OUTPUT_SEQ[119].real=119.000000, OUTPUT_SEQ[119].img=0.000000
[09:42:34.620] ifft: OUTPUT_SEQ[120].real=120.000000, OUTPUT_SEQ[120].img=0.000000
[09:42:34.700] ifft: OUTPUT_SEQ[121].real=121.000000, OUTPUT_SEQ[121].img=0.000000
[09:42:34.764] ifft: OUTPUT_SEQ[122].real=122.000000, OUTPUT_SEQ[122].img=0.000000
[09:42:34.828] ifft: OUTPUT_SEQ[123].real=123.000000, OUTPUT_SEQ[123].img=0.000000
[09:42:34.908] ifft: OUTPUT_SEQ[124].real=124.000000, OUTPUT_SEQ[124].img=0.000000
[09:42:34.971] ifft: OUTPUT_SEQ[125].real=125.000000, OUTPUT_SEQ[125].img=0.000000
[09:42:35.051] ifft: OUTPUT_SEQ[126].real=126.000000, OUTPUT_SEQ[126].img=0.000000
[09:42:35.116] ifft: OUTPUT_SEQ[127].real=127.000000, OUTPUT_SEQ[127].img=0.000000
4. 小结
(1)使用FPU可以加快运算,该实例中大概快了200/0.7=286倍
(2)这个实例中的fft是浮点fft,并且是算法的直接实现,没有做任何优化,计算三角函数会耗时很长,实际应用过程中,可直接使用CMSIS的DSP库。里面的fft,iir/fir滤波器以及各种数学运算库都已经是针对ST系列芯片做了很好的优化,方便快速实现和开发算法。