Reinforcement Learning with Code 【Code 4. Vanilla DQN】
Reinforcement Learning with Code 【Code 4. Vanilla DQN】
This note records how the author begin to learn RL. Both theoretical understanding and code practice are presented. Many material are referenced such as ZhaoShiyu’s Mathematical Foundation of Reinforcement Learning.
The code refers to Mofan’s reinforcement learning course and Hands on Reinforcement Learning.
文章目录
- Reinforcement Learning with Code 【Code 4. Vanilla DQN】
-
- 序
- 1. Theoretical Basis
- 2. Gym Env
- 3. Vanilla DQN with Code
- 4. Reference
序
最初掀起深度强化学习热潮的辨识David Silver所在的DeepMind团队所研究的DQN算法,随着DQN算法的推出,很多对于DQN改进的算法也纷纷亮相,并在实验中取得了不错的成绩。
DQN算法是传统强化学习算法Q-Learning算法引入神经网络的改进,即神经网络其实是用来估计状态-动作值q-value的,另外还有一个要求是DQN所解决的问题中环境的动作空间必须的离散的。
其中,最基本的DQN算法被称为Vanilla DQN,即是本文实现的算法。Vanilla DQN 的主要思想是使用一个深度神经网络来近似 Q 函数,这个函数用于估计在给定状态下选择不同动作的累积奖励。这个网络将状态作为输入,并输出每个动作的 Q 值。然后,智能体根据 Q 值来选择行动,通常使用 ε-贪婪(ε-greedy)策略,在探索和利用之间进行平衡。
训练 Vanilla DQN 需要解决两个主要问题:
- 经验回放(Experience Replay): 为了解决数据之间的相关性问题,Vanilla DQN 使用经验回放,将智能体的经验存储在一个经验池中,并从中随机采样用于训练。
- 目标网络(Target Network): 为了增加稳定性,Vanilla DQN 使用两个神经网络:一个是用于选择动作的主网络,另一个是用于计算目标 Q 值的目标网络。目标网络的参数会定期从主网络中复制,以减少训练中的波动。
尽管 Vanilla DQN 在解决许多强化学习问题上取得了成功,但它也有一些局限性,如在处理连续动作空间、训练不稳定等方面存在一些挑战。后续的算法,如 Double DQN、Dueling DQN、Rainbow DQN 等,对 Vanilla DQN 进行了改进,以解决这些问题,并在深度 Q 网络领域取得了更好的性能。
1. Theoretical Basis
Readers can get some insight understanding from (Chapter 8. Value Function Approximation), which is omitted here.
这里还是简要介绍一下DQN的思想,就是用一个神经网络来近似值函数(value function),根据Q-learning的思想,我们已经使用 r + γ max a q ( s , a , w ) r+\gamma\max_a q(s,a,w) r+γmaxaq(s,a,w)来近似了真值,当我们使用神经网络来近似值函数时,我们用符号 q ^ \hat{q} q^来表示对q-value的近似。
则我们需要优化的目标函数是
min w J ( w ) = E [ ( R + γ max a ∈ A ( S ′ ) q ^ ( S ′ , a , w ) − q ^ ( S , A , w ) ) 2 ] {\min_w J(w) = \mathbb{E} \Big[ \Big( R+\gamma \max_{a\in\mathcal{A}(S^\prime)} \hat{q}(S^\prime, a, w) - \hat{q}(S,A,w) \Big)^2 \Big]} wminJ(w)=E[(R+γa∈A(S′)maxq^(S′,a,w)−q^(S,A,w))2]
详细的解释见下图,或则见(Chapter 8. Value Function Approximation)。

这里涉及到了两个技巧,第一个就是Experience replay,第二个技巧是Two Networks。
-
Experience replay: 主要是需要维护一个经验池,在一般的有监督学习中,假设训练数据是独立同分布的,我们每次训练神经网络的时候从训练数据中随机采样一个或若干个数据来进行梯度下降,随着学习的不断进行,每一个训练数据会被使用多次。在原来的 Q-learning 算法中,每一个数据只会用来更新一次值。为了更好地将 Q-learning 和深度神经网络结合,DQN 算法采用了经验回放(experience replay)方法,具体做法为维护一个回放缓冲区,将每次从环境中采样得到的四元组数据(状态、动作、奖励、下一状态)存储到回放缓冲区中,训练 Q 网络的时候再从回放缓冲区中随机采样若干数据来进行训练。这么做可以起到以下两个作用。
-
使样本满足独立假设。在 MDP 中交互采样得到的数据本身不满足独立假设,因为这一时刻的状态和上一时刻的状态有关。非独立同分布的数据对训练神经网络有很大的影响,会使神经网络拟合到最近训练的数据上。采用经验回放可以打破样本之间的相关性,让其满足独立假设。
-
提高样本效率。每一个样本可以被使用多次,十分适合深度神经网络的梯度学习。
-
-
Two Networks: DQN算法的最终更新目标是让 q ^ ( s , a , w ) \hat{q}(s,a,w) q^(s,a,w)逼近 r + γ max a q ^ ( s , a , w ) r+\gamma\max_a\hat{q}(s,a,w) r+γmaxaq^(s,a,w),由于 TD 误差目标本身就包含神经网络的输出,因此在更新网络参数的同时目标也在不断地改变,这非常容易造成神经网络训练的不稳定性。为了解决这一问题,DQN 便使用了目标网络(target network)的思想:既然训练过程中 Q 网络的不断更新会导致目标不断发生改变,不如暂时先将 TD 目标中的 Q 网络固定住。为了实现这一思想,我们需要利用两套 Q 网络。
- 原来的训练网络 q ^ ( s , a , w ) \hat{q}(s,a,w) q^(s,a,w),用于计算原来的损失函数 q ^ ( S , A , w ) \hat{q}(S,A,w) q^(S,A,w)中的项,并且使用正常梯度下降方法来进行更新。
- 目标网络的参数用 w T w^T wT来表示,训练网络参数用 w w w来表示,目标网络参数 w T w^T wT用于计算原先损失函数中的项。如果两套网络的参数随时保持一致,则仍为原先不够稳定的算法。为了让更新目标更稳定,目标网络并不会每一步都更新。具体而言,目标网络使用训练网络的一套较旧的参数,训练网络 q ^ ( s , a , w ) \hat{q}(s,a,w) q^(s,a,w)在训练中的每一步都会更新,而目标网络的参数每隔 C C C步才会与训练网络 w w w同步一次,即 w T ← w w^T\leftarrow w wT←w。这样做使得目标网络相对于训练网络更加稳定。而训练网络按照一下方式进行更新
w t + 1 = w t + α t [ r t + 1 + γ max a ∈ A ( s t + 1 ) q ^ ( s t + 1 , a , w T ) − q ^ ( s t , a t , w ) ] ∇ w q ^ ( s t , a t , w ) \textcolor{red}{w_{t+1} = w_{t} + \alpha_t \Big[ r_{t+1} + \gamma \max_{a\in\mathcal{A}(s_{t+1})} \hat{q}(s_{t+1},a,w_T) - \hat{q}(s_t,a_t,w) \Big] \nabla_w \hat{q}(s_t,a_t,w)} wt+1=wt+αt[rt+1+γa∈A(st+1)maxq^(st+1,a,wT)−q^(st,at,w)]∇wq^(st,at,w)
2. Gym Env
本文使用gym库中的CartPole-v1作为智能体的交互环境,其目的是左右移动小车,让小车上的木棍能够尽可能保持竖直。所以动作空间为离散值,只有向左 and 向右。但状态空间是连续的,则这种情况下不能使用tabular的表示方式。CartPole-v1的action_space和state_space的设置如下,详见gym官网
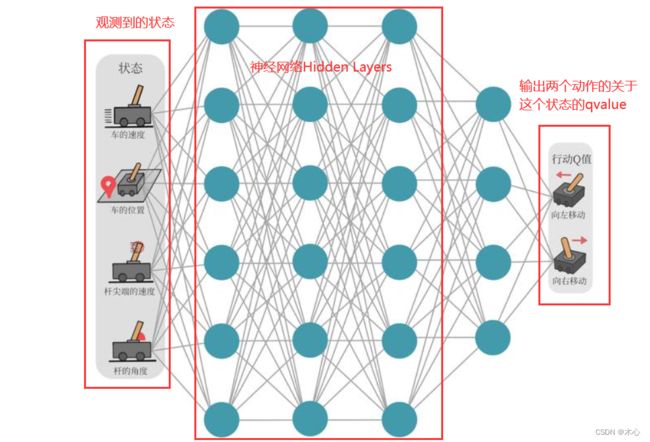
这个环境下,动作空间是离散的二维,状态空间是连续的4维,分别表示小车的位置,小车的速度,杆的角度,杆的角速度。
当我们使用值函数近似的时候,我们用神经网络来拟合值函数,对于给定的状态 s s s,我们输出关于这个状态 s s s的所有动作的action value,在这个例子中即是 q ^ ( s , 向左 ) \hat{q}(s,向左) q^(s,向左)和 q ^ ( s , 向右 ) \hat{q}(s,向右) q^(s,向右),如下图所示
CartPole-v1环境的奖励函数设置如下:杆每保持竖直1s奖励+1,奖励的最大阈值为475。
环境的结束条件包括:
- 杆的角度超过 ± 12 ° \pm 12\degree ±12°
- 车的位置超过 ± 2.4 \pm 2.4 ±2.4
- 环境运行超过了 500 500 500步,所以当每步的奖励为 + 1 +1 +1时,最大的奖励就是 500 × 1 = 500 500 \times 1=500 500×1=500
3. Vanilla DQN with Code
import random
import collections
import torch
import torch.nn.functional as F
import numpy as np
from tqdm import tqdm
import gym
import matplotlib.pyplot as plt
# Experience Replay
class ReplayBuffer():
def __init__(self, capacity):
self.buffer = collections.deque(maxlen=capacity)
def size(self):
return len(self.buffer)
def add(self, state, action, reward, next_state, done):
self.buffer.append((state, action, reward, next_state, done))
def sample(self, batch_size):
transition = random.sample(self.buffer, batch_size)
states, actions, rewards, next_states, dones = zip(*transition)
return np.array(states), np.array(actions), np.array(rewards), np.array(next_states), np.array(dones)
# Value Approximation Net
class QNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(QNet,self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
def forward(self,x):
x = F.relu(self.fc1(x))
x = self.fc2(x)
return x
# Deep Q-Learning Algorithm
class DQN():
def __init__(self, state_dim, hidden_dim, action_dim, learning_rate,
gamma, epsilon, target_update, device):
self.action_dim = action_dim
self.q_net = QNet(state_dim, hidden_dim, action_dim).to(device) # behavior net将计算转移到cuda上
self.target_q_net = QNet(state_dim, hidden_dim, action_dim).to(device) # target net
self.optimizer = torch.optim.Adam(self.q_net.parameters(), lr=learning_rate)
self.target_update = target_update # 目标网络更新频率
self.gamma = gamma # 折扣因子
self.epsilon = epsilon # epsilon-greedy
self.count = 0 # record update times
self.device = device # device
def choose_action(self, state): # epsilon-greedy
# one state is a list [x1, x2, x3, x4]
if np.random.random() < self.epsilon:
action = np.random.randint(self.action_dim) # 产生[0,action_dim)的随机数作为action
else:
state = torch.tensor([state], dtype=torch.float).to(self.device)
action = self.q_net(state).argmax(dim=1).item()
return action
def learn(self, transition_dict):
states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions'], dtype=torch.int64).view(-1,1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1,1).to(self.device)
dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1,1).to(self.device)
q_values = self.q_net(states).gather(dim=1, index=actions)
max_next_q_values = self.target_q_net(next_states).max(dim=1)[0].view(-1,1)
q_target = rewards + self.gamma * max_next_q_values * (1 - dones) # TD target
dqn_loss = torch.mean(F.mse_loss(q_target, q_values)) # 均方误差损失函数
self.optimizer.zero_grad()
dqn_loss.backward()
self.optimizer.step()
# 一定周期后更新target network参数
if self.count % self.target_update == 0:
self.target_q_net.load_state_dict(
self.q_net.state_dict())
self.count += 1
# train on off-policy agent
def train_on_off_policy_agent(env, agent, replaybuffer, num_episodes, batch_size, minimal_size, seed):
return_list = []
for i in range(10):
with tqdm(total=int(num_episodes/10), desc="Iteration %d"%(i+1)) as pbar:
for i_episode in range(int(num_episodes/10)):
episode_return = 0
observation, _ = env.reset(seed=seed)
done = False
while not done:
env.render()
action = agent.choose_action(observation)
observation_, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
replaybuffer.add(observation, action, reward, observation_, done)
observation = observation_
episode_return += reward
if replaybuffer.size() > minimal_size:
b_s, b_a, b_r, b_ns, b_d = replaybuffer.sample(batch_size)
transition_dict = {
'states': b_s,
'actions': b_a,
'rewards': b_r,
'next_states': b_ns,
'dones': b_d
}
# print('\n--------------------------------\n')
# print(transition_dict)
# print('\n--------------------------------\n')
agent.learn(transition_dict)
return_list.append(episode_return)
if (i_episode + 1) % 10 == 0:
pbar.set_postfix({
'episode':
'%d' % (num_episodes / 10 * i + i_episode + 1),
'return':
'%.3f' % np.mean(return_list[-10:])
})
pbar.update(1)
env.close()
return return_list
def plot_curve(return_list, algorithm_name, env_name):
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('{} on {}'.format(algorithm_name, env_name))
plt.show()
def moving_average(a, window_size):
# moving_average滑动平均
cumulative_sum = np.cumsum(np.insert(a, 0, 0))
middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_size
r = np.arange(1, window_size-1, 2)
begin = np.cumsum(a[:window_size-1])[::2] / r
end = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]
return np.concatenate((begin, middle, end))
if __name__ == "__main__":
# reproducible
seed_number = 0
random.seed(seed_number)
np.random.seed(seed_number)
torch.manual_seed(seed_number)
# render or not
render = False
env_name = 'CartPole-v1'
if render:
env = gym.make(id=env_name, render_mode='human')
else:
env = gym.make(id=env_name)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
hidden_dim = 128 # number of hidden layers
lr = 2e-3 # learning rate
num_episodes = 500 # episode length
gamma = 0.98 # discounted rate
epsilon = 0.01 # epsilon-greedy
target_update = 10 # per step to update target network
buffer_size = 10000 # maximum size of replay buffer
minimal_size = 500 # minimum size of replay buffer to begin learning
batch_size = 64 # batch_size using to train the neural network
device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')
agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon, target_update, device)
replaybuffer = ReplayBuffer(buffer_size)
return_list = train_on_off_policy_agent(env, agent, replaybuffer, num_episodes, batch_size, minimal_size, seed_number)
plot_curve(return_list, 'DQN', env_name)
mv_return = moving_average(return_list, 9)
plot_curve(mv_return, 'DQN', env_name)
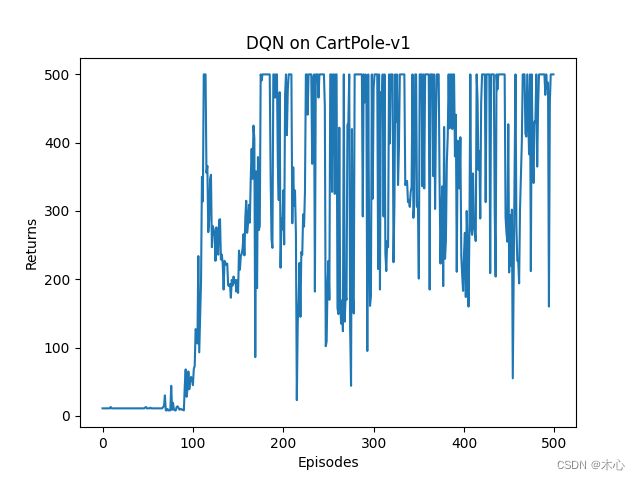
最终学习曲线如图所示
将曲线进行滑动平均后
4. Reference
赵世钰老师的课程
莫烦ReinforcementLearning course
Chapter 8. Value Function Approximation
Hands on RL
DQN及其多种变式