Dropout、剪枝、正则化有什么关系？什么是Dropout？

$$Dropout、剪枝、正则化有什么关系？$$

-----前言

上次打球和同学聊天时聊起Dropout和剪枝有什么区别，似乎并没有什么不同？
我想了一下，做出了一下思考：$$首先Dropout和pruning都属于Redundancy-awareoptimization里模型级别的去冗余的工作，dropout就是training的过程中只加载一部分神经元，防止过拟合，而pruning只是剪掉一部分unimportant的参数，本身目的并不是为了防止过拟合，又快又简单的压缩才是目的，同时又不掉精度。所以两者差别还是挺大的。$$
而且pruning之后一般精度是会下降的，但dropout的时候accuracy本身就是为了防止overfitting，所以会提高，$区别在于，在Dropout中，每个参数都有可能在训练阶段被丢弃，但在推理阶段会回来。但在剪枝后，参数在剪枝后会被永远丢弃，在训练和推理阶段都不再需要$。$且Dropout随机地将一些神经元的输出值置为0，这就是一个最简单最没有规律的剪枝思路。$

---

关系：$$首先明确一点，Dropout、正则化都是防止过拟合的方法。和剪枝本身是两码事，剪枝是一个独立的领域，思路万千，前两者都只是训练过程中的一种手段。$$

另外，在早期的工作中，网络剪枝被证明是降低网络复杂性和过拟合的有效方法。

• 出自2016年Hanson教授发表的这篇《Deep compression》. In early work, network pruning proved to be a valid way to reduce the network complexity and over-fitting (LeCun et al., 1989;Hanson & Pratt, 1989; Hassibi et al., 1993; Strom, 1997).
   

1. Dropout、正则化

避免过拟合的方法有：early stopping、数据集扩增（Data augmentation）、正则化（L0/L1/L2（L2 regularization也叫weight decay）），dropout等。

正则化方法：L0/L1/L2 regularization及其变形等。例如$$J(\theta )=\frac{1}{2m}[\sum _{i=1}^m(h_{\theta }^{(x^i)}-y^i{)}^2+\lambda \sum _{j=1}^n{\theta }_j^2]$$就是对目标函数做优化的时候，减小${\theta }_j$的影响，然后$minJ(\theta )$，
 
后面的$\lambda {\sum }_{j=1}^n{\theta }_j^2$就是一个正则项，$\lambda$为正则化系数。
 
而Dropout就是随机初始化一些神经元，并不加载全部由的神经元，往往用于提高模型的泛化能力，防止过拟合，对于过拟合的理解，这里我也稍微记录一下，防止以后忘了。
 
对于过拟合这个词在网上一搜，我们可以很方便地得到这个答案：如果一个网络的训练集精度很高而测试集精度很低，那么我们称这个模型是过拟合的。那更深一点地理解呢？网上还会给出一个曲线，类似于这样

 
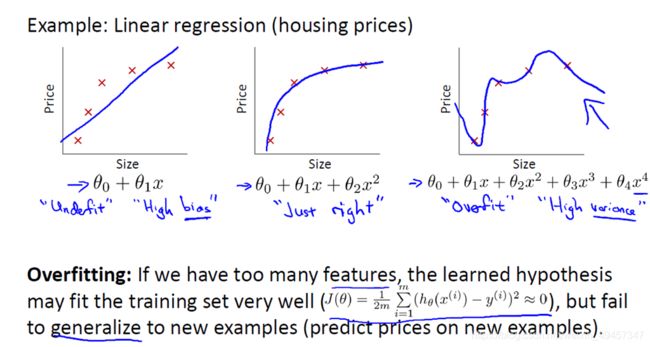
那这最右边的叫做过拟合，而我们过拟合的通俗意义的理解究竟是什么呢？就是学习到的特征太多，模型对每个变量都非常敏感，导致任意一个变量发生一点变化了，结果都会不一样，从而与Groundtruth出入很大，在图中对应的就是波动得很快。
 
从另一个方面理解，就从它的文字定义上仔细思考一下——它在训练集上精度很好，而在测试集上表现不佳，那这还叫深度学习吗? 我觉得你恐怕是深度背书？咱是不是有另一种可能，你这个模型只是把训练集上的特征都记住了，所以你在训练集上都认得请，而陌生的图片它不认识，它之前没有背过，所以他就不能“考高分”了，通俗地说，这个模型似乎就像只会背题，不会把只是融会贯通的应试考生，这样是无法把考试考好的。题海战术是让你多做题，有手感，把知识点融会贯通，并不是让你记住所有练习题。

那回到我们上面的说法，既然模型对每个变量都非常敏感，也就是考虑的变量太多了，而其实由于剪枝我们早就认识到，深度网络模型中是有很多冗余的，在我复现的过程中发现channel剪掉60%都能finetune回原来的精度，可见原始模型中是有多少没用的特征。

那我们把他对主要特征的考虑权重放大，但我们不只知道哪些特征是不重要的，所以我们就把其余的特征都乘以一个极小的系数$\lambda$,这样网络不仅考虑了所有的变量，又不会过于影响它的判断，这就是正则化。
 
 

2. 什么是Dropout？

dropout 从字面意思就是‘踢掉’，‘退掉’。
那丢掉的是什么呢？
我们来看看：

2.1 -----Superidot的笑容

我们拿一张Superidot的笑容为例：

这张放这么大是为了展示细节？对，是这样的

上面图片清晰明亮，大家应该看出这是谁吧

我们的模型根据这张输入图片，一步一步提取特征，也能够认出来，但是其中包含了很多冗余的信息，比如我们的羽服，抹胸，手镯，并不是我们进行人脸识别所需的特征。

那这些冗余的特征，会不会影响我们的判断呢？实际上会，但人脸的识别最终还是取决于脸部特征：

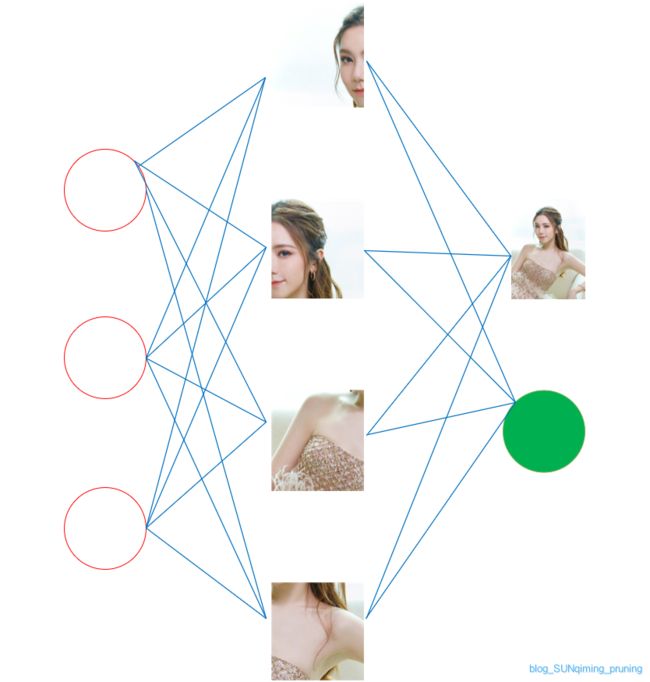
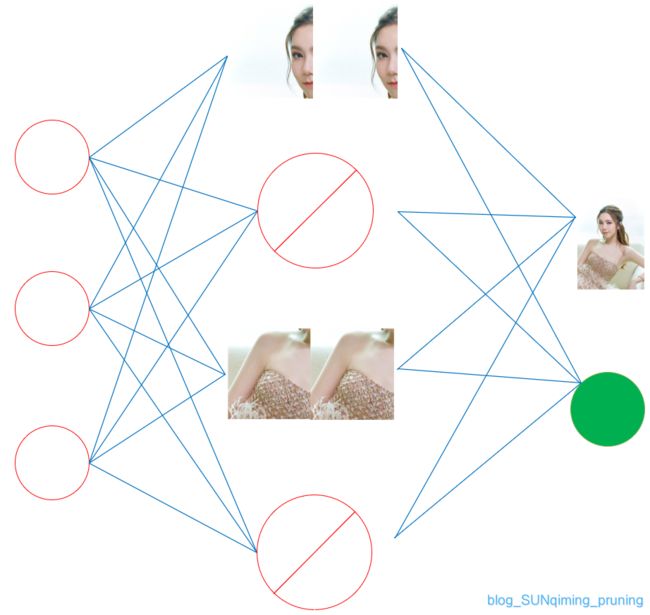
好的，那我们现在开始丢了，我们丢掉一些特征，如下：

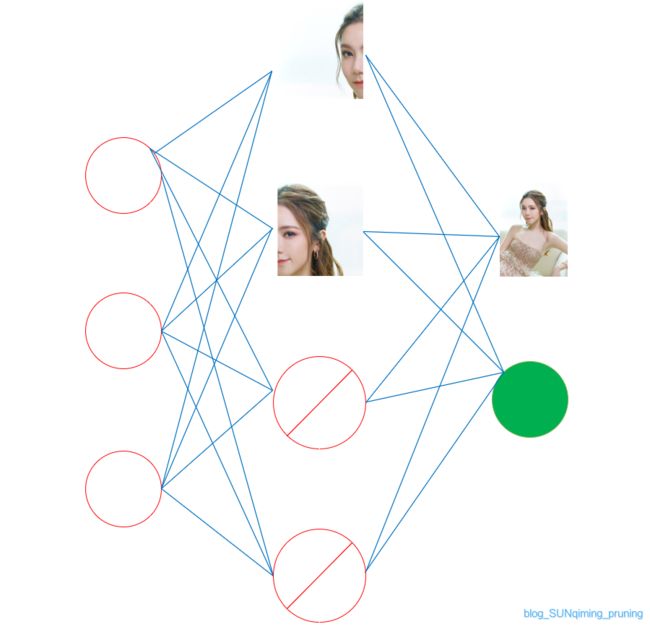
现在机器还能识别出紫棋吗？答案是还能，所以模型和我们人一样，还是可以识别出这个人。而实际上我们训练过程中也是这么做的，把一些多余的特征去掉，避免学习过多的特征出现过拟合现象。从而使得模型更鲁棒。

(小红圈里加斜线表示不参与计算)

简单来说，认人，看脸就可，装饰、穿着，是不需要的特征。

但这样必须保留完整的脸才行，拿我们中间的四张小图来说，必须左右脸同时提取，才能作出判断，模型似乎并不鲁棒。而输入一半的脸和一半的肩膀，还能识别吗？我们就来试一试：

再随机抽取一半的神经元，不让他们参与任何计算，也不参与到权重的更新，比如这样

只认右脸和右肩膀呢？

甚至只认肩（xiong）膀：

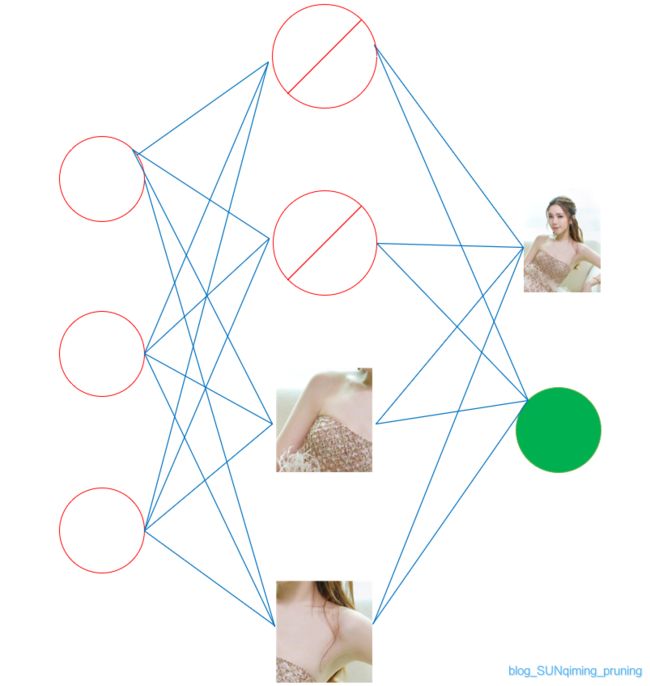
又会怎么样呢？
 
显然我们只看xiong是看不出是ziqi的，这种情况就是dropout rate设置太大，我们这是0.5，在训练的时候可能丢掉了重点特征，造成模型过拟合了。

当然有些同学说，老师老师，根据我多年阅人无数的经验，我认得出来

所以控制好dropout rate也是调参的关键，调好了就是加大模型鲁棒性，调不好便会过拟合。

一般情况下，dropout rate 设为0.3-0.5即可
 
所以你看，每次训练都随机让一定神经元停止参与运算，简单的操作让我们由一个模型演变成四个模型：

 
1个模型的作用效果，也转变成4个模型的效果和，更像一个多模型投票
 
所以，虽然第四个模型overfitting了，但是前三个也模型参与投票判断，第四个模型overfitting就被弱化了
 
所以，dropout的出现，使得模型稳定性和鲁棒性被大大提高了。

 
 
到这，你应该是理解dropout 的原理和作用了，但是还有关键的一步
 
那就是训练的时候会停止训练一些神经元，但是测试的时候，整个模型是完整，可不会dropout 任何神经元啊
 
这样就出现了一个问题，就好比
 
平时是羽毛球双打，比赛时候突然发现报的是单打，自然不会有好成绩。

---

 

那我们说了，dropout的作用本来就是不断地尝试去掉一些特征看看识别的鲁棒性，而train阶段可以dropout，但测试时还是这么多大的模型，并没有起到dropout神经元的作用，

 
所以，在训练的时候，我们会对没有被dropout的神经元权值做一个rescale，也就是补充一部分的特征，只是为了在测试的时候还是适应的。

也就是这样
 

 
 
而没用dropout的神经网络前向传播公式：
$$z_i^{(l+1)}=w_i^{(l+1)}\cdot y^l+b_i^{(l+1)},$$
$$y_i^{(l+1)}=f(z_i^{(l+1)})$$
 
用了dropout 的神经网络前向传播计算公式：
$$r_j^{(l)}\sim Bernoulli(p),$$
$$y^{(l)}=r^{(l)}\ast y^{(l)},$$
$$z_i^{(l+1)}=w_i^{(l+1)}{y}^{(l)},$$
$$y_i^{(l+1)}=f(z_i^{(l+1)}).$$

就是在训练的时候就做rescale，至少可以一定程度上‘弥补’测试中没有使用dropout所带来的问题。

如果有小伙伴们还有不清楚的，可以看看谷歌官方专利上的解释：谷歌官方解释

 
 

3. 总结

以上就是今天要讲的内容，本文仅仅简单介绍了dropout的使用，而dropout能让我们训练模型的时候避免出现过拟合的现象。