1. 深度学习——激活函数

机器学习面试题汇总与解析——激活函数

本章讲解知识点

• 1. 什么是激活函数？
• 2. 为什么要使用激活函数？
• 3. 详细讲解激活函数

---

• 本专栏适合于Python已经入门的学生或人士，有一定的编程基础。
• 本专栏适合于算法工程师、机器学习、图像处理求职的学生或人士。
• 本专栏针对面试题答案进行了优化，尽量做到好记、言简意赅。这才是一份面试题总结的正确打开方式。这样才方便背诵
• 如专栏内容有错漏，欢迎在评论区指出或私聊我更改，一起学习，共同进步。
• 相信大家都有着高尚的灵魂，请尊重我的知识产权，未经允许严禁各类机构和个人转载、传阅本专栏的内容。

• 关于机器学习算法书籍，我强烈推荐一本《百面机器学习算法工程师带你面试》，这个就很类似面经，还有讲解，写得比较好。

• 关于深度学习算法书籍，我强烈推荐一本《解析神经网络——深度学习实践手册》，简称 CNN book，通俗易懂。

---

1. 什么是激活函数？

1.1 定义与作用

激活函数是一种用于神经网络和其他机器学习模型中的非线性函数。它被应用于神经网络的每个神经元上，将输入信号进行转换，产生输出信号。激活函数的作用是引入非线性性质，使神经网络能够学习和表示更复杂的函数关系。

在神经网络中，每个神经元接收来自上一层神经元的加权输入，然后通过激活函数对这个加权输入进行非线性变换，生成神经元的输出。这个输出被传递到下一层神经元作为输入。

激活函数的主要作用有以下几点：

• 引入非线性：激活函数能够将线性变换后的输入转换为非线性输出，使得神经网络具备非线性建模能力。这对于解决复杂的非线性问题至关重要。

• 改善模型的表达能力：通过引入非线性性质，激活函数能够增加神经网络的表达能力，使其能够学习和表示更加复杂的函数关系。

• 增强网络的稳定性：激活函数能够限制神经元输出的范围，防止信号的过度扩散或衰减，从而增强神经网络的稳定性和收敛性。

1.2 常见的激活函数包括

• Sigmoid函数（逻辑斯蒂函数）
• 双曲正切函数（Tanh函数）
• ReLU函数（修正线性单元）
• Leaky ReLU函数
• Parametric ReLU函数（PReLU）
• ELU函数（指数线性单元）
• Softmax函数（用于多分类任务）

选择适当的激活函数取决于具体的问题和网络架构。不同的激活函数具有不同的性质和适用场景，因此在设计神经网络时需要根据实际情况进行选择。

2. 为什么要使用激活函数？

下图是神经元模型：

其中 $x_i$ 为第 i 个输入，$w_i$ 为第 i 个神经元的权重，$\theta$ 为门限。可以看到，$y$ 为线性函数，线性函数就只能处理线性问题，非线性的问题没办法处理了。所以为了让神经网络也能处理非线性的问题，才需要引入非线性激活函数，把线性函数给非线性化。这就是使用激活函数的意义。

让我们以一个简单的线性函数和一个非线性函数作为例子，来说明为什么要使用激活函数。

假设我们有一个神经网络，其中包含一个输入层和一个输出层。我们使用一个线性函数作为激活函数，并尝试使用这个网络进行二分类任务。

• 线性函数作为激活函数：
  如果我们选择线性函数作为激活函数（例如f(x) = ax），那么整个神经网络的输出就是一个线性函数。无论我们网络有多少层，它仍然只能表示线性关系。这意味着网络无法学习和表示复杂的非线性模式，对于解决复杂的问题效果会非常有限。

• 非线性函数作为激活函数：
  现在，我们选择一个非线性函数作为激活函数，例如ReLU函数（f(x) = max(0, x)）。这个非线性函数引入了非线性性质，使得神经网络能够学习和表示更复杂的函数关系。ReLU函数在输入为负数时输出为0，在输入为正数时输出与输入相等，这样的非线性特性可以帮助网络区分不同类别的数据，并提高分类准确性。

举个例子，假设我们的二分类任务是将两类数据点分开，这两类数据点在输入空间中呈现出一个圆环状的分布。如果我们使用线性函数作为激活函数，无论多少层网络，它只能拟合一条直线，无法切割出圆环形状的区域。但是，如果我们使用ReLU等非线性函数作为激活函数，神经网络可以通过学习组合多个线性函数，来逼近并拟合出圆环形状的边界，从而更好地进行分类。

如下图数据，线性函数是没办法很好二分类的，但是非线性函数可以逼近并拟合出圆环形状的边界，从而更好地进行分类，例如数据被分类成蓝色部分和黄色部分。

3. 详细讲解激活函数

从激活函数的发展历史开始讲起：

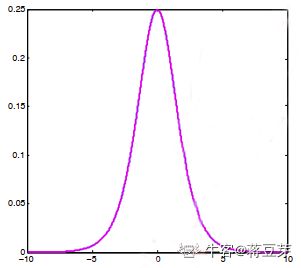
3.1 sigmoid 函数

1.定义

sigmoid 函数，sigmoid(x) 型函数也称 Logistic 函数，公式如下：

$$\begin{gathered} \sigma (x)=\frac{1}{1+exp(-x)} \\ \text{\hspace{1em}(.)} \end{gathered}$$

sigmoid 型函数是第一个被广泛应用于神经网络的激活函数。经过 sigmoid 型函数作用后，输出的值范围在 [0,1] 之间。但是 sigmoid 型函数的输出存在均值不为 0 的情况，并且存在梯度消失的问题，在深层网络中被其他激活函数替代。在逻辑回归中使用的该激活函数用于输出分类。

2.期望

函数图形如下：

从函数和公式可以很清楚地看到，sigmoid 函数将输入映射到了 [0,1] 之间，因为输出都大于 0，所以 sigmoid 函数期望（均值）大于 0 的。什么意思呢？简单理解就是 (0+1)/2=0.5，均值大于 0。如果输出区间在 [-1,1] 之间，那么均值就是 (-1+1)/2=0 了。

当然这只是简单理解，期望计算公式如下：

$$E(x)=\sum _{k=1}^{\infty }{x}_k{p}_k\text{\hspace{1em}(.)}$$

这个 $x_k$ 表示取值，如 1,2,3,4…；$p_k$ 表示取值的概率，按照上面的公式加和，就得到我们的期望 $E(x)$ 了。

然后在神经网络中，我们希望当前一层的神经元输出均值为 0，为什么要均值为 0 呢？有以下几点原因：

• 均值中心化：将激活函数的期望值设置为 0 可以使得网络的输出更容易进行归一化处理。通过均值中心化，可以减少输入数据的偏移和不平衡，有助于提高网络的稳定性和收敛速度。

• 梯度传播：激活函数的期望为 0 可以促使梯度在反向传播过程中更好地传播。当激活函数的期望为非零值时，梯度的平均值可能会发生偏移，导致梯度传播过程中的不稳定性。而期望为 0 的激活函数可以使得梯度在不同层之间的传播更加一致和稳定。

• 防止梯度爆炸和梯度消失：激活函数的期望为 0 有助于缓解梯度爆炸和梯度消失的问题。如果激活函数的期望值较大，网络的参数更新可能会导致梯度变得非常大，造成梯度爆炸。相反，如果激活函数的期望值较小，梯度可能会在反向传播过程中逐渐消失，导致梯度消失问题。通过将激活函数的期望设置为0，可以在一定程度上避免这些问题。

sigmoid 函数期望显然不满足以上原则。

3.梯度消失

sigmoid 函数存在梯度消失的问题。

那怎么又存在梯度消失的问题呢？梯度是啥啊？梯度就是曲线斜率吧，曲线斜率就是切线吧，大家可以回忆一下高中的知识哈，在函数图形上画切线就可以看到 sigmoid 函数两边的斜率已经越来越趋向 0 了，如图：

都趋向 0 了，我们神经网络反向传播参数的时候参数就不更新了呀，不更新就代表网络没有继续学习了，这就是梯度消失。

4.Sigmoid 函数的特点如下

• 输出范围：Sigmoid 函数的输出范围在 0 和 1 之间，可以将输出解释为概率值，表示某个事件发生的概率。

• 平滑性：Sigmoid 函数具有平滑的连续性质，其曲线在整个定义域内都是光滑且单调递增的。方便求导，能求导就可以使用梯度下降的方式来优化。

• 中心对称性：Sigmoid函数关于 $y=0.5$ 对称，即对于任意 $x$，有 $f(-x)=1-f(x)$。

• 饱和性：当输入值非常大或非常小时，Sigmoid 函数的输出接近于 1 或 0，导致梯度接近于 0。这种饱和性可能导致梯度消失的问题，在深度神经网络中容易出现梯度衰减问题。

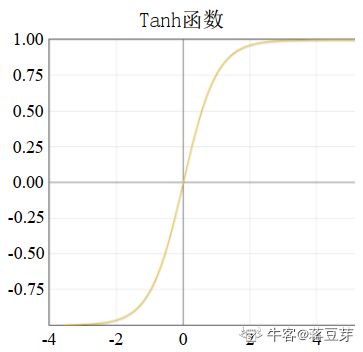
3.2 tanh 函数

tanh 函数。tanh(x) 型函数可以解决 sigmoid 型函数的期望（均值）不为 0 的情况。函数输出范围为 (-1,+1)。但 tanh(x) 型函数依然存在梯度消失的问题。公式如下：

$$\begin{gathered} tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{e^{2x}-1}{e^{2x}+1}=2\cdot sigmoid(2x)-1 \\ \text{\hspace{1em}(.)} \end{gathered}$$

在 LSTM 中使用了 tanh(x) 型函数。

可以看到函数曲线：

输出范围成了 [-1,1]，期望（均值）为 0。梯度消失的问题同sigmoid。

tanh 函数的特点如下：

• 输出范围：tanh函数的输出范围在 -1 和 1 之间，可以将输出解释为样本属于不同类别的置信度或概率。

• 平滑性：tanh函数具有平滑的连续性质，其曲线在整个定义域内都是光滑且单调递增的。

• 中心对称性：tanh 函数关于原点对称，即对于任意 $x$，有 $f(-x)=-f(x)$。输出期望为 0。

• 饱和性：当输入值非常大或非常小时，tanh 函数的输出接近于 1 或 -1，导致梯度接近于 0。这种饱和性可能导致梯度消失的问题，在深度神经网络中容易出现梯度衰减问题。

3.3 ReLU 函数

ReLU 函数。ReLU(x) 型函数可以有效避免梯度消失的问题，公式如下：

$$\begin{gathered} ReLU(x)=\{\begin{array}{l}x,ifx\ge 0\\ 0,ifx<0\end{array} \\ \text{\hspace{1em}(.)} \end{gathered}$$

函数如图：

可以看到，ReLU 在大于 0 时，斜率固定，不存在梯度消失的问题，这有助于网络训练。再看看梯度函数：

ReLU 梯度稳定，值还比 sigmoid 大，所以可以加快网络训练。不过 ReLU 的缺点就是小于 0 的值不再得到响应，这又不利于网络训练。我们在输入图像时就要注意，应该使用 Min-Max 归一化，而不能使用 Z-score 归一化。

ReLU 函数的特点如下：

• 线性性质：在输入为正时，ReLU 函数是线性函数，直接将输入值传递给输出。这使得 ReLU 函数具有较强的表达能力。

• 非线性性质：在输入为负时，ReLU 函数输出为 0，引入了非线性特性，可以帮助神经网络学习更复杂的模式和表示。

• 稀疏激活：ReLU 函数的输出为 0 的特性使得神经网络中的神经元具有稀疏激活性。对于给定的输入样本，只有部分神经元会被激活，从而减少了参数的冗余性，提高了网络的效率。

• 消失梯度问题的缓解：相比于 Sigmoid 函数和 tanh 函数，在反向传播过程中，ReLU 函数的梯度计算更简单且不会出现饱和现象，因此更不容易出现梯度消失的问题。

• 死区现象：ReLU 函数在输入为负时输出为 0，可能导致神经元死亡的问题，即一旦激活为 0，对应的权重将不再更新，该神经元很可能包含重要特征。

• 梯度爆炸：ReLU 不会对数据做幅度压缩，如果数据的幅度不断扩张，模型层数越深，幅度扩张越厉害，出现梯度爆炸，最终会影响模型性能。

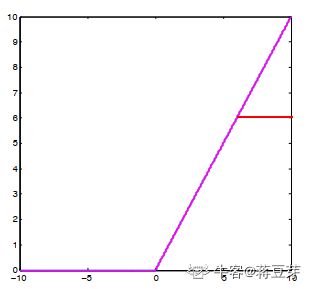
3.4 ReLU6 函数

大家可以注意到 ReLU 的正值输出为 [0,无穷大]，关键是我们计算机内存有限，能存储无穷大的数吗？当然不能，同时为了对 ReLU 的数据做幅度压缩，所以将 ReLU 应用到实际中时需要限定输出的最大值，所以就成了 ReLU6 了，如图：

就是因为最大输出限定在 6，所以称为 ReLU6 了。

3.5 Leaky ReLU 函数

Leaky ReLU 函数。Leaky ReLU(x) 型函数为负值增加了一个斜率，缓解了“死区”现象，公式如下：

$$\begin{gathered} LeakyReLU(x)=\{\begin{array}{l}x,ifx\ge 0\\ \alpha \cdot x,ifx<0\end{array} \\ \text{\hspace{1em}(.)} \end{gathered}$$

$\alpha$ 是一个小的正数，通常取接近于 0 的小值，如 0.01。

Leaky ReLU函数如图：

可以看到，0 的左边存在斜率，那么负值也可以得到响应，有利于网络学习到更多的信息。Leaky ReLU(x) 型函数缺点是，超参数 $\alpha$ 合适的值不好设定。当我们想让神经网络能够学到负值信息，那么使用该激活函数。

Leaky ReLU函数的特点如下：

• 线性性质：在输入为正时，Leaky ReLU 函数与 ReLU 函数一样，直接输出输入值，具有线性性质。

• 非线性性质：在输入为负时，Leaky ReLU 函数乘以斜率 $\alpha$，引入了非线性特性，可以帮助神经网络学习更复杂的模式和表示。

• 缓解神经元死亡问题：通过引入一个小的斜率 $\alpha$，Leaky ReLU 函数使得负值部分不再完全变为 0，从而缓解了神经元死亡问题。即使输入为负，梯度仍然可以传播并更新相关的权重。

• 零中心性：当斜率 $\alpha$ 取较小的正数时，Leaky ReLU 函数在整个定义域上保持零中心性，有助于网络的稳定性和收敛性。

3.6 Mish 函数

Mish 激活函数。Mish 激活函数同样允许负值有一定的梯度流入。公式如下：

$$\begin{gathered} Mish(x)=x\cdot tanh(log(1+e^x)) \\ \text{\hspace{1em}(.)} \end{gathered}$$

应用场景同 Leaky ReLU(x) 型函数。

如图：

可以看出，在负值中，允许有一定的梯度流入。

3.7 PReLU 函数

参数化 ReLU（P-ReLU）。参数化 ReLU 为了解决超参数 $\alpha$ 合适的值不好设定的问题，干脆将这个参数也融入模型的整体训练过程中。也使用误差反向传播和随机梯度下降的方法更新参数。

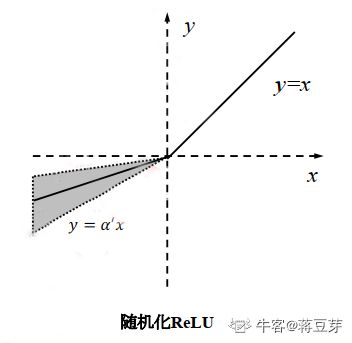
3.8 RReLU 函数

随机化 ReLU（R-ReLU）。顾名思义，就是超参数 $\alpha$ 随机化，让不同的层自己学习不同的超参数，但随机化的超参数的分布符合均值分布或高斯分布，如图：

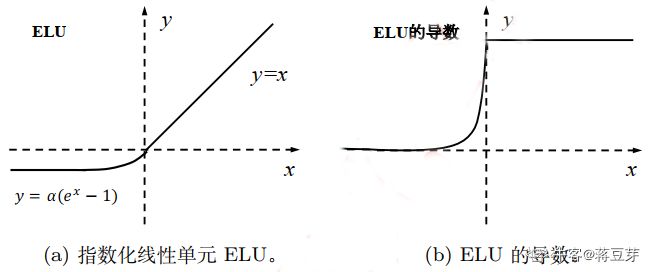
3.9 指数化线性单元（ELU）

指数化线性单元（ELU）。也是为了解决死区问题，公式如下：

$$\begin{gathered} ELU(x)=\{\begin{array}{l}x,ifx\ge 0\\ \lambda \cdot (e^x-1),ifx<0\end{array} \\ \text{\hspace{1em}(.)} \end{gathered}$$

如图：

缺点是指数计算量大。

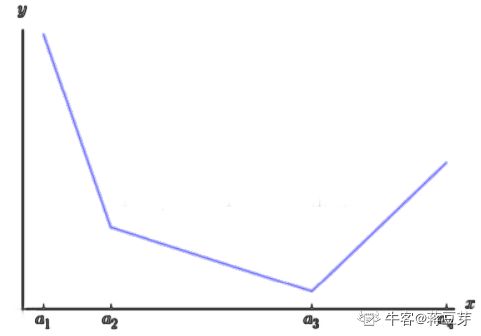
3.10 Maxout

Maxout。与常规的激活函数不同，Maxout 是一个可以学习的分段线性函数。其原理是，任何 ReLU 及其变体等激活函数都可以看成分段的线性函数，而 Maxout 加入的一层神经元正是一个可以学习参数的分段线性函数。Maxout 是深度学习网络中的一层网络，就像池化层、卷积层一样等，我们可以把 Maxout 看成是网络的激活函数层。如图：

从图中可以看出，Maxout 就像一个层一样，k 个节点就对应 k 个参数。这个层最终表现为一个分段函数。

优点是其拟合能力很强，理论上可以拟合任意的凸函数。缺点是参数量激增！在 Network-in-Network 中使用的该激活函数。

3.11 Softmax 函数

Softmax 函数是一种常用的激活函数，常用于多类别分类任务中，Softmax 函数将输入向量转化为一个概率分布，使得各个类别的输出概率之和为 1。这样可以将模型的输出解释为样本属于各个类别的概率。Softmax 不用于神经网络的中间层，而是在最后的输出时使用。

公式如下：

$$s=softmax(z)=\frac{e^{z_i}}{{\sum }_{k=1}^K{e}^{z_k}},i=1,2,...K\text{\hspace{1em}(.)}$$

Softmax 是用于多类分类问题的激活函数，在多类分类问题中，超过两个类标签则需要类成员关系。对于长度为 K 的任意实向量，Softmax 可以将其压缩为长度为 K，值在（0，1）范围内，并且向量中元素的总和为 1 的实向量。

右边的概率加起来为 1

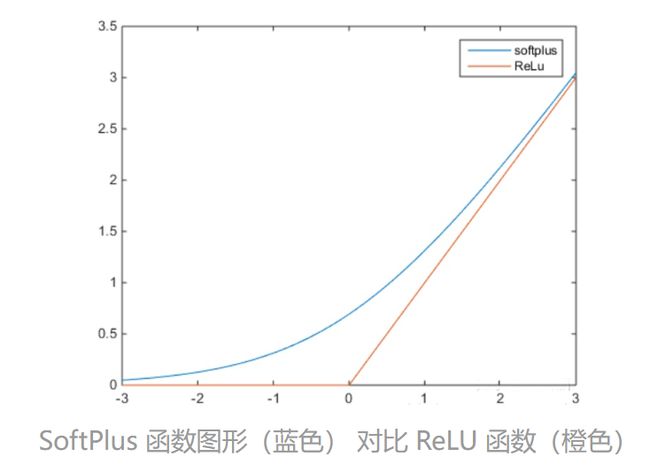
3.12 Softplus 函数

SoftPlus 相当于是对 ReLU 的平滑，解决了 Dead ReLU 问题。

$$\begin{gathered} Softplus(x)=lo{g}_e(1+e^x) \\ \text{\hspace{1em}(.)} \end{gathered}$$

3.13 总结

在隐藏层中使用推荐的顺序：ReLU / Leaky-ReLU > ELU > Tanh > Sigmoid

CNN 中 ReLU 使用较多

RNN 中 Tanh、sigmoid 使用较多

LSTM 中门机制使用 sigmoid，计算 cell 的时候用 tanh

---

面试题

1. 说一下你了解的激活函数？分别应用于什么场景？⭐⭐⭐⭐⭐

参考回答

1.sigmoid。sigmoid(x) 型函数也称 Logistic 函数，公式如下：

$$\begin{gathered} \sigma (x)=\frac{1}{1+exp(-x)} \\ \text{\hspace{1em}(.)} \end{gathered}$$

sigmoid 型函数是第一个被广泛应用于神经网络的激活函数。经过 sigmoid 型函数作用后，输出的值范围在 [0,1] 之间。但是 sigmoid 型函数的输出存在均值不为 0 的情况，并且存在梯度消失的问题，在深层网络中被其他激活函数替代。在逻辑回归中使用的该激活函数用于输出分类。

2.tanh。tanh(x) 型函数可以解决 sigmoid 型函数的期望（均值）不为 0 的情况。函数输出范围为 (-1,+1)。但 tanh(x) 型函数依然存在梯度消失的问题。公式如下：

$$\begin{gathered} tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{e^{2x}-1}{e^{2x}+1}=2\cdot sigmoid(2x)-1 \\ \text{\hspace{1em}(.)} \end{gathered}$$

在 LSTM 中使用了 tanh(x) 型函数。

3.ReLU。ReLU(x) 型函数可以有效避免梯度消失的问题，公式如下：

$$\begin{gathered} ReLU(x)=\{\begin{array}{l}x,ifx\ge 0\\ 0,ifx<0\end{array} \\ \text{\hspace{1em}(.)} \end{gathered}$$

ReLU(x) 型函数的缺点是负值成为“死区”，神经网络无法再对其进行响应。Alex-Net 使用了 ReLU(x) 型函数。当我们训练深层神经网络时，最好使用 ReLU(x) 型函数而不是 sigmoid(x) 型函数。

4.Leaky ReLU。Leaky ReLU(x) 型函数为负值增加了一个斜率，缓解了“死区”现象，公式如下：

$$\begin{gathered} LeakyReLU(x)=\{\begin{array}{l}x,ifx\ge 0\\ \alpha \cdot x,ifx<0\end{array} \\ \text{\hspace{1em}(.)} \end{gathered}$$

Leaky ReLU(x) 型函数缺点是，超参数 $\alpha$ 合适的值不好设定。当我们想让神经网络能够学到负值信息，那么使用该激活函数。

5.Mish 激活函数。Mish 激活函数同样允许负值有一定的梯度流入。公式如下：

$$\begin{gathered} Mish(x)=x\cdot tanh(log(1+e^x)) \\ \text{\hspace{1em}(.)} \end{gathered}$$

应用场景同 Leaky ReLU(x) 型函数。

6.参数化 ReLU（P-ReLU）。参数化 ReLU 为了解决超参数 $\alpha$ 合适的值不好设定的问题，干脆将这个参数也融入模型的整体训练过程中。也使用误差反向传播和随机梯度下降的方法更新参数。

7.随机化 ReLU（R-ReLU）。顾名思义，就是超参数 $\alpha$ 随机化，让不同的层自己学习不同的超参数，但随机化的超参数的分布符合均值分布或高斯分布。

8.指数化线性单元（ELU）。也是为了解决死区问题，公式如下：

$$\begin{gathered} ELU(x)=\{\begin{array}{l}x,ifx\ge 0\\ \lambda \cdot (e^x-1),ifx<0\end{array} \\ \text{\hspace{1em}(.)} \end{gathered}$$

缺点是指数计算量大。

9.Maxout。与常规的激活函数不同，Maxout 是一个可以学习的分段线性函数。其原理是，任何 ReLU 及其变体等激活函数都可以看成分段的线性函数，而 Maxout 加入的一层神经元正是一个可以学习参数的分段线性函数。

优点是其拟合能力很强，理论上可以拟合任意的凸函数。缺点是参数量激增！在 Network-in-Network 中使用的该激活函数。

10.Softmax 函数是一种常用的激活函数，常用于多类别分类任务中，Softmax 函数将输入向量转化为一个概率分布，使得各个类别的输出概率之和为 1。Softmax 不用于神经网络的中间层，而是在最后的输出时使用。

公式如下：

$$s=softmax(z)=\frac{e^{z_i}}{{\sum }_{k=1}^K{e}^{z_k}},i=1,2,...K\text{\hspace{1em}(.)}$$

11.SoftPlus 相当于是对 ReLU 的平滑，解决了 Dead ReLU 问题。

$$\begin{gathered} Softplus(x)=lo{g}_e(1+e^x) \\ \text{\hspace{1em}(.)} \end{gathered}$$

2. 说说你平时都用过什么激活函数，各自什么特点？⭐⭐⭐⭐⭐

参考回答

回答与第一题类似。

3. 写一下 leaky ReLU 的公式，跟 ReLU 比有什么优势？⭐⭐⭐⭐⭐

参考回答

Leaky ReLU。Leaky ReLU(x) 型函数为负值增加了一个斜率，缓解了 ReLU(x) “死区”现象，公式如下：

$$\begin{gathered} LeakyReLU(x)=\{\begin{array}{l}x,ifx\ge 0\\ \alpha \cdot x,ifx<0\end{array} \\ \text{\hspace{1em}(.)} \end{gathered}$$

Leaky ReLU(x) 型函数缺点是，超参数 $\alpha$ 合适的值不好设定。当我们想让神经网络能够学到负值信息，那么使用该激活函数。

4. 了解 ReLU6 吗？⭐⭐⭐⭐⭐

参考回答

ReLU的正值输出为[0,无穷大]，关键是我们计算机内存有限，能存储无穷大的数吗？当然不能，同时为了对 ReLU 的数据做幅度压缩，所以将 ReLU 应用到实际中时需要限定输出的最大值，所以就成了 ReLU6 了，如图：

就是因为最大输出限定在 6，所以称为 ReLU6 了。

5. sigmoid 有什么缺点，有哪些解决办法？⭐⭐⭐⭐⭐

参考回答

sigmoid 型函数是第一个被广泛应用于神经网络的激活函数。经过 sigmoid 型函数作用后，输出的值范围在 [0,1] 之间。但是 sigmoid 型函数的输出存在均值不为 0 的情况，并且存在梯度消失与梯度爆炸的问题。

解决办法

1. 在深层网络中被其他激活函数替代。如 ReLU(x)、Leaky ReLU(x) 等

2. 在分类问题中，sigmoid 做激活函数时，使用交叉熵损失函数替代均方误差损失函数。

3. 采用正确的权重初始化方法：如 He_init 方法

4. 加入 BN 层

5. 分层训练权重

6. ReLU 在零点可导吗，不可导如何进行反向传播？⭐⭐⭐⭐⭐

参考回答

不可导。

人为将梯度规定为 0.

答案解析

caffe源码~/caffe/src/caffe/layers/relu_layer.cpp倒数第十行代码：

bottom_diff[i] = top_diff[i] * ((bottom_data[i] > 0)+ negative_slope * (bottom_data[i] <= 0));

可以清楚看到，默认情况下（negative_slope=0），间断点处（<=0）的导数认为是 0.

7. 推导 sigmoid 求导公式⭐⭐⭐⭐⭐

参考回答

sigmoid公式为：

$$\begin{gathered} \sigma (x)=\frac{1}{1+exp(-z)} \\ \text{\hspace{1em}(.)} \end{gathered}$$

那么求导推导如下：

$$\begin{gathered} {\sigma }^{{}^{\prime }}(x)=(\frac{1}{1+e^{-z}}{)}^{{}^{\prime }} \\ =\frac{1}{(1+e^{-z}{)}^2}\cdot (e^{-z}) \\ =\frac{1}{1+e^{-z}}\cdot \frac{e^{-z}}{1+e^{-z}} \\ =\frac{1}{1+e^{-z}}\cdot (1-\frac{1}{1+e^{-z}}) \\ =\sigma (z)(1-\sigma (z)) \\ \text{\hspace{1em}(.)} \end{gathered}$$

8. Softmax 公式，Softmax 溢出怎么处理⭐⭐⭐⭐⭐

参考回答

Softmax 公式：

$$s=softmax(z)=\frac{e^{z_i}}{{\sum }_{k=1}^K{e}^{z_k}},i=1,2,...K\text{\hspace{1em}(.)}$$

为了处理 Softmax 溢出问题，可以进行以下操作：

• 常数平移：对输入向量中的每个元素减去其最大值。这样做可以确保指数函数的输入不会过大，减少数值溢出的风险。例如，对于输入向量 $x$，进行常数平移操作后得到 $x_{shifted}$：$x_{shifted}=x-max(x)$，操作类似 Min-Max 归一化。

• 数值稳定化：在计算 Softmax 函数时，使用数值稳定化的公式，将指数函数的输入除以其最大值。这可以避免指数函数的输入过大，减少溢出的可能性。例如，对于经过常数平移的输入向量 $x_{shifted}$，计算 Softmax 函数的输出 $y$：
  $y=exp(x_{shifted})/sum(exp(x_{shifted}))$

9. Softmax 公式求导⭐⭐⭐⭐⭐

参考回答

首先 softmax 公式如下：

$$s=softmax(z)=\frac{e^{z_i}}{{\sum }_{k=1}^K{e}^{z_k}},i=1,2,...K\text{\hspace{1em}(.)}$$

求导：

1. 当 $j\ne i$，那么：

$$\begin{gathered} \frac{\partial s_j}{\partial z_i}=\frac{\partial (\frac{e^{z_j}}{{\sum }_{j=1}^K{e}^{z_k}})}{\partial z_i} \\ =-e^{z_j}\cdot \frac{1}{({\sum }_{k=1}^K{e}^{z_k}{)}^2}\cdot e^{z_i} \\ =-\frac{e^{z_j}}{{\sum }_{k=1}^K{e}^{z_k}}\cdot \frac{e^{z_i}}{{\sum }_{k=1}^K{e}^{z_k}} \\ =-s_j{s}_i \\ \text{\hspace{1em}(.)} \end{gathered}$$

2. 当 $j=i$，那么：

$$\begin{gathered} \frac{\partial s_j}{\partial z_i}=\frac{\partial s_i}{\partial z_i}=\frac{\partial (\frac{e^{z_i}}{{\sum }_{k=1}^K{e}^{z_k}})}{\partial z_i} \\ =\frac{e^{z_i}{\sum }_{k=1}^K{e}^{z_k}-(e^{z_i}{)}^2}{({\sum }_{k=1}^K{e}^{z_k}{)}^2} \\ =\frac{e^{z_i}}{{\sum }_{k=1}^K{e}^{z_k}}\cdot \frac{{\sum }_{k=1}^K{e}^{z_k}-e^{z_i}}{{\sum }_{k=1}^K{e}^{z_k}} \\ =\frac{e^{z_i}}{{\sum }_{k=1}^K{e}^{z_k}}\cdot (1-\frac{e^{z_i}}{{\sum }_{k=1}^K{e}^{z_k}}) \\ =s_i(1-s_i) \\ \text{\hspace{1em}(.)} \end{gathered}$$

答案解析

更多内容参考文章：https://blog.csdn.net/qian99/article/details/78046329

10. 激活函数的定义与作用⭐⭐⭐⭐⭐

激活函数是一种用于神经网络和其他机器学习模型中的非线性函数。它被应用于神经网络的每个神经元上，将输入信号进行转换，产生输出信号。激活函数的作用是引入非线性性质，使神经网络能够学习和表示更复杂的函数关系。

11. 神经网络输出均值为 0 的好处，哪些激活函数均值为 0？⭐⭐⭐⭐

在神经网络中，我们希望当前一层的神经元输出均值为 0，为什么要均值为 0 呢？有以下几点原因：

• 均值中心化：将激活函数的期望值设置为0可以使得网络的输出更容易进行归一化处理。通过均值中心化，可以减少输入数据的偏移和不平衡，有助于提高网络的稳定性和收敛速度。

• 梯度传播：激活函数的期望为0可以促使梯度在反向传播过程中更好地传播。当激活函数的期望为非零值时，梯度的平均值可能会发生偏移，导致梯度传播过程中的不稳定性。而期望为0的激活函数可以使得梯度在不同层之间的传播更加一致和稳定。

• 防止梯度爆炸和梯度消失：激活函数的期望为0有助于缓解梯度爆炸和梯度消失的问题。如果激活函数的期望值较大，网络的参数更新可能会导致梯度变得非常大，造成梯度爆炸。相反，如果激活函数的期望值较小，梯度可能会在反向传播过程中逐渐消失，导致梯度消失问题。通过将激活函数的期望设置为0，可以在一定程度上避免这些问题。

tanh 函数均值为 0

11. Sigmoid 函数的特点⭐⭐⭐⭐⭐

• 输出范围：Sigmoid 函数的输出范围在 0 和 1 之间，可以将输出解释为概率值，表示某个事件发生的概率。

• 平滑性：Sigmoid 函数具有平滑的连续性质，其曲线在整个定义域内都是光滑且单调递增的。方便求导，能求导就可以使用梯度下降的方式来优化。

• 中心对称性：Sigmoid函数关于 $y=0.5$ 对称，即对于任意 $x$，有 $f(-x)=1-f(x)$。

• 饱和性：当输入值非常大或非常小时，Sigmoid 函数的输出接近于 1 或 0，导致梯度接近于 0。这种饱和性可能导致梯度消失的问题，在深度神经网络中容易出现梯度衰减问题。

12. ReLU 函数的特点⭐⭐⭐⭐⭐

• 线性性质：在输入为正时，ReLU 函数是线性函数，直接将输入值传递给输出。这使得 ReLU 函数具有较强的表达能力。

• 非线性性质：在输入为负时，ReLU 函数输出为 0，引入了非线性特性，可以帮助神经网络学习更复杂的模式和表示。

• 稀疏激活：ReLU 函数的输出为 0 的特性使得神经网络中的神经元具有稀疏激活性。对于给定的输入样本，只有部分神经元会被激活，从而减少了参数的冗余性，提高了网络的效率。

• 消失梯度问题的缓解：相比于 Sigmoid 函数和 tanh 函数，在反向传播过程中，ReLU 函数的梯度计算更简单且不会出现饱和现象，因此更不容易出现梯度消失的问题。

• 死区现象：ReLU 函数在输入为负时输出为 0，可能导致神经元死亡的问题，即一旦激活为 0，对应的权重将不再更新，该神经元很可能包含重要特征。

• 梯度爆炸：ReLU 不会对数据做幅度压缩，如果数据的幅度不断扩张，模型层数越深，幅度扩张越厉害，出现梯度爆炸，最终会影响模型性能。

12. Softmax 函数的应用场景⭐⭐⭐⭐⭐

Softmax 函数是一种常用的激活函数，常用于多类别分类任务中，Softmax 函数将输入向量转化为一个概率分布，使得各个类别的输出概率之和为 1。这样可以将模型的输出解释为样本属于各个类别的概率。Softmax 不用于神经网络的中间层，而是在最后的输出时使用。

13. 为什么需要使用非线性激活函数而不是线性激活函数？⭐⭐⭐⭐

1. 非线性模拟能力：神经网络的目标是学习非线性关系和复杂的模式。如果使用线性激活函数，多个线性层的组合仍然只会产生一个线性函数，无法表示更复杂的非线性关系。

2. 解决异或问题：异或是一个经典的非线性问题，用线性函数无法准确地拟合异或函数。通过引入非线性激活函数，如 ReLU、Sigmoid 或 Tanh，可以实现神经网络对异或问题的学习。

3. 激活函数的导数：非线性激活函数具有非零的导数，这对于反向传播算法和梯度下降优化非常重要。线性激活函数的导数恒为常数，不具有区分不同输入值的能力，这会导致反向传播中梯度无法传递有效的信息，从而影响网络的学习能力。

4. 增加非线性特性：通过引入非线性激活函数，神经网络可以引入更多的非线性特性。这有助于模型学习更复杂的模式、表达更丰富的特征表示，并提高模型的泛化能力。

14. 在训练神经网络时，选择激活函数有什么考虑因素？⭐⭐⭐⭐

在训练神经网络时选择激活函数时，有几个考虑因素需要注意：

1. 非线性性：激活函数应该是非线性的，以便神经网络可以学习和表示复杂的非线性关系。线性激活函数只能实现线性模型，无法捕捉非线性模式。

2. 梯度消失和爆炸：某些激活函数可能导致梯度消失或梯度爆炸的问题。梯度消失指的是在反向传播中，梯度逐渐变小，导致较远层的权重更新缓慢。梯度爆炸则是梯度变得非常大，导致数值不稳定和训练困难。选择激活函数时，应该考虑其梯度的稳定性，避免梯度消失或爆炸问题，特别是深度很深的神经网络。

3. 可微性：激活函数应该是可微的，以便能够进行反向传播和梯度计算。可微性是训练神经网络的关键要求，因为梯度下降等优化算法依赖于梯度计算来更新权重。

4. 计算效率：某些激活函数可能计算复杂度较高，导致网络训练速度变慢。在实际应用中，需要考虑激活函数的计算效率，特别是在大型神经网络和大规模数据集上进行训练时。

5. 具体任务需求：不同的任务可能对激活函数有不同的要求。例如，对于二分类任务，Sigmoid 函数通常被用作输出层的激活函数，Softmax 函数用于多分类任务的最后一层神经元的激活函数。而在图像分类任务中，ReLU 及其变体常被用作隐藏层的激活函数。

15. 在自然语言处理（NLP）任务中，常用的激活函数有哪些？⭐⭐⭐⭐

• Tanh（双曲正切函数）：Tanh函数将输入值映射到 [-1, 1] 的范围内，对于文本分类和情感分析等任务非常常见。Tanh 函数具有对称性和可导性，能够保留输入的正负性和非线性关系。

• Sigmoid 函数：Sigmoid 函数将输入值映射到 [0, 1] 的范围内，常用于二分类问题和概率估计。在 NLP 任务中，它经常用于情感分析、命名实体识别等任务中作为输出层的激活函数，将输出转化为概率。

• Softmax 函数：Softmax 函数主要用于多类别分类问题，将多个输出值归一化为概率分布。在NLP任务中，例如文本分类和机器翻译中，Softmax 函数常用于输出层的激活函数，将网络的输出转化为各个类别的概率。