二叉搜索树
文章目录
- 二叉搜索树
-
- 二叉搜索树的概念
- 二叉搜索树的操作
-
- 插入操作
-
- 非递归插入
- 递归插入
- 删除操作
-
- 非递归删除
- 递归删除
- 查找操作
-
- 非递归查找
- 递归查找
- 测试用例
- 中序遍历
- 完整代码
- 程序运行结果
- 难点
二叉搜索树
二叉搜索树的概念
二叉搜索树又称二叉排序树,或者是空树或者是具有以下性质的二叉树
1 若左子树非空,则左子树上所有节点关键字值均小于根节点的关键字
2 若右子树非空,则右子树上所有节点关键字值均大于根节点的关键字
3 左右子树本身也分别是一棵二叉排序树
4 二叉排序树没有相同值的节点存在
二叉搜索树的操作
插入操作
在二叉树中进行插入操作时,首先要检测该元素是否在树中,若以存在,则不进行插入,若不存在,才进行插入
插入步骤:
1 如果节点为根节点,则直接插入
2 如果树不为空,则比较关键字的值和左右子树的值,如果小于根节点,则插入左子树,如果大于根节点,则插入右子树
非递归插入
//二叉搜索树的非递归创建
void BST_Create(BiTree &T,int x)
{
if(T == nullptr) //对根节点特殊处理
T = new BitNode(x);
else
{
BiTree cur = T;
BiTree parent = T;
while(cur) //寻找要插入的位置,保存要插入位置的双亲节点
{
parent = cur;
if(cur->val > x)
cur = cur->lchild;
else if(cur->val < x)
cur = cur->rchild;
else
return;
}
BiTree tmp = new BitNode(x);
if(parent->val > x) //判断插入节点是左子树还是右子树
parent->lchild = tmp;
else
parent->rchild = tmp;
}
}递归插入
//二叉搜索树的递归插入
void BST_RE_Create(BiTree &T,int x) //这里传入的是根节点的引用,因为在创建过程中需要修改根节点
{
if(T == nullptr)
T = new BitNode(x);
if(T->val > x)
BST_RE_Create(T->lchild,x);
else if(T->val < x)
BST_RE_Create(T->rchild,x);
else
return;
}删除操作
在二叉树中进行删除时,首先要判断要删除的节点是否在树中,如果不在,则直接返回,若存在,则进行如下操作:
1 如果删除的节点没有左子树,则将该节点的右子树赋值给该节点的双亲节点
2 如果删除的节点没有右子树,则将该节点的左子树赋值给该节点的双亲节点
3 如果删除的节点既有左子树又有右子树,则在该节点的右子树中寻找一个最小值进行替换,进而删除最小值节点(或者可以在该节点的左子树中寻找一个最大的节点,再删除这个最大节点)
非递归删除
//二叉搜索树的非递归删除
void BST_Delete(BiTree &T,int x)
{
if(T == nullptr)
return;
BiTree parent = T;
BiTree cur = T;
while(cur) //寻找要删除的节点
{
if(cur->val == x)
break;
else if(cur->val > x)
{
parent = cur;
cur = cur->lchild;
}
else
{
parent = cur;
cur = cur->rchild;
}
}
if(cur->lchild == nullptr) //该节点没有左孩子,将他的右子树接上去
{
if(parent->lchild == cur)
parent->lchild = cur->rchild;
else
parent->rchild = cur->rchild;
}
else if(cur->rchild == nullptr) //该节点没有右孩子,将他的左子树接上去
{
if(parent->lchild == cur)
parent->lchild = cur->lchild;
else
parent->rchild = cur->lchild;
}
else //该节点既有左孩子又有右孩子,找出他的右孩子的最小节点,进行替换
{
BiTree tmp = cur->rchild;
parent = cur;
while(tmp->lchild) //寻找右孩子的最小节点
{
parent = tmp;
tmp = tmp->lchild;
}
cur->val = tmp->val; //替换
if(parent->lchild == tmp) //接右孩子,需要注意,因为它的左孩子已经走到尽头了
parent->lchild = tmp->rchild;
else
parent->rchild = tmp->rchild;
cur = tmp;
}
delete cur; //别忘记释放内存
}递归删除
//二叉搜索树的递归删除
void BST_RE_Delete(BiTree &T,int x)
{
if(T == nullptr)
return;
if(T->val > x) //递归寻找要删除的节点
BST_RE_Delete(T->lchild,x);
else if(T->val < x)
BST_RE_Delete(T->rchild,x);
else
{
BiTree cur = T; //找到要删除的节点,对节点进行保存,以便删除
if(T->lchild == nullptr) //要删除节点的左子树为空,让该节点等于它的右子树
{
T = T->rchild;
delete cur;
}
else if(T->rchild == nullptr) //要删除节点的右子树为空,让该节点等于它的左子树
{
T = T->lchild;
delete cur;
}
else //要删除的节点既有左子树,又有右子树
{
BiTree tmp = cur->rchild; //保存该节点的右孩子节点
while(tmp->lchild) //在右子树中找寻最小的节点
tmp = tmp->lchild;
cur->val = tmp->val; //将找到的最小节点赋值给要删除的节点
BST_RE_Delete(cur->rchild,tmp->val); //递归删除最小节点
}
}
}查找操作
查找操作比较简单,将关键字与根节点进行比较,如果相同,则返回,如果根节点值小于关键字,则在右子树中查找,反之,则在左子树中查找。
非递归查找
//二叉搜索树的非递归查找
bool BST_Search(BiTree T,int x)
{
if(T)
{
BiTree cur = T;
while(cur)
{
if(cur->val == x)
return true;
else if(cur->val > x)
cur = cur->lchild;
else
cur = cur->rchild;
}
}
return false;
}递归查找
//二叉搜索树的递归查找
bool BST_RE_Search(BiTree T,int x)
{
if(T)
{
if(T->val == x)
return true;
else if(T->val > x)
return BST_RE_Search(T->lchild,x);
else
return BST_RE_Search(T->rchild,x);
}
return false;
}测试用例
//创建随机的测试数据,返回不重复的随机数,num为测试数据个数
vector<int> randVector(int num) {
vector<int> result;
result.clear();
result.reserve(num);
srand((int)time(0));
for (int i = 0; i < num; i++)
{
result.push_back(i);
}
int p1;
int p2;
int temp;
while (--num)
{
p1 = num;
p2 = rand() % num;
temp = result[p1];
result[p1] = result[p2];
result[p2] = temp;
}
return result;
}中序遍历
二叉搜索树的中序遍历结果是呈递增排序的序列
//中序遍历(递归方式)
void InOrder(BiTree T)
{
if(T)
{
InOrder(T->lchild);
cout << T->val << " ";
InOrder(T->rchild);
}
}完整代码
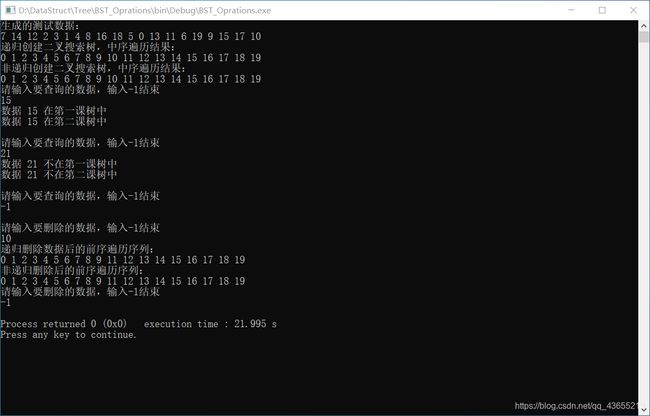
#include 程序运行结果
难点
重要的是理清思路,分析清楚每一种可能的情况,在删除操作时,面对被删除节点同时存在左右子树问题时,将最小或最大子树替换后,对这个最小或最大子树进行删除时,子树的节点有两种情况,这个一定要理清楚。
参考文档主要是:
https://blog.csdn.net/zhao_miao/article/details/82312723
但是这篇文档中有一点错误,是在非递归删除有左右子树的节点时有一点错误。