【高等数学】导数的应用
导数的应用
- 1、洛必达法则
-
- 1.1、引例
- 1.2、内容
- 1.3、证明
- 1.4、洛必达的应用
-
- 总结
- 1.5、注意
- 2、泰勒公式
-
- 2.1、解决的问题
- 2.2、引例
- 2.3、内容
-
- 2.3.1、带Peano余项的泰勒公式
- 2.3.2、带Lagrange余项的泰勒公式
- 2.3.3、麦克劳林公式
- 2.3.4、几个初等函数的麦克劳林公式
- 2.4、证明
- 2.5、泰勒公式的应用
- 2.6、总结
- 3、函数的单调性
-
- 3.1、函数单调性的判别方法
- 3.2、证明
- 3.3、应用
- 4、曲线的凹凸性与拐点
-
- 4.1、定义
- 4.2、证明
- 4.3、拐点
- 5、函数的极值和最值
-
- 5.1、极值
- 5.2、最大值与最小值问题
- 6、曲线的渐近线
- 7.函数图像的描绘
- 8、曲率
-
- 8.1、弧微分
-
- 8.1.1、弧微分推导
- 8.1.2、弧微分的几何意义
- 8.2、曲率及其计算公式
-
- 8.2.1、曲率
- 8.2.2、曲率计算公式
- 8.2.3、曲率圆与曲率半径
![]()
1、洛必达法则
1.1、引例
例如: lim x → 0 x − sin x x 3 \lim_{x \to 0}\frac{x-\sin x}{x^3} limx→0x3x−sinx
【解】
令 f ( x ) = x − sin x , g ( x ) = x 3 f(x)=x-\sin x,g(x)=x^3 f(x)=x−sinx,g(x)=x3
根据柯西中值定理:
lim x → 0 ( x − sin x ) − ( 0 − sin 0 ) x 3 − 0 3 = f ′ ( ξ ) g ′ ( ξ ) = 1 − cos ξ 3 ξ 2 \lim_{x \to 0}\frac{(x-\sin x)-(0-\sin 0)}{x^3-0^3}=\frac{f'(\xi)}{g'(\xi)}=\frac{1-\cos \xi}{3\xi^2} limx→0x3−03(x−sinx)−(0−sin0)=g′(ξ)f′(ξ)=3ξ21−cosξ
∵ 0 < ξ < x ∵0<\xi
∴ lim x → 0 1 − cos x 3 x 2 = 1 − cos ξ 3 ξ 2 ∴\lim_{x \to 0}\frac{1-\cos x}{3x^2}=\frac{1-\cos \xi}{3\xi^2} ∴limx→03x21−cosx=3ξ21−cosξ
lim x → 0 1 − cos x 3 x 2 = 1 2 x 2 3 x 2 = 1 6 \lim_{x \to 0}\frac{1-\cos x}{3x^2}=\frac{\frac{1}{2}x^2}{3x^2}=\frac{1}{6} limx→03x21−cosx=3x221x2=61
观察上述解法,本质上来说其实是对函数的分子分母分别进行求导操作,最终能得到极限,这也就是洛必达法则的思想
1.2、内容
若:
(1)、 lim x → x 0 f ( x ) = lim x → x 0 g ( x ) = 0 / ∞ \lim_{x \to x_0}f(x)=\lim_{x \to x_0}g(x)=0/∞ limx→x0f(x)=limx→x0g(x)=0/∞
(2)、 f ( x ) f(x) f(x)和 g ( x ) g(x) g(x)在 U ˚ ( x 0 , δ ) \mathring U(x_0,\delta) U˚(x0,δ)内可导,且 g ′ ( x ) ≠ 0 g'(x)≠0 g′(x)=0
(3)、 lim x → x 0 f ′ ( x ) g ′ ( x ) \lim_{x \to x_0}\frac{f'(x)}{g'(x)} limx→x0g′(x)f′(x)存在(或 ∞ ∞ ∞)
则:
lim x → x 0 f ( x ) g ( x ) = lim x → x 0 f ′ ( x ) g ′ ( x ) \lim_{x \to x_0}\frac{f(x)}{g(x)}=\lim_{x \to x_0}\frac{f'(x)}{g'(x)} x→x0limg(x)f(x)=x→x0limg′(x)f′(x)
1.3、证明
因为极限讨论的是趋近于某点的值,而与这一点的函数值无关,所以我们可以根据需要设置这一点的函数值
设 f ( x 0 ) = g ( x 0 ) = 0 f(x_0)=g(x_0)=0 f(x0)=g(x0)=0
lim x → x 0 f ( x ) g ( x ) = lim x → x 0 f ( x ) − f ( x 0 ) g ( x ) − g ( x 0 ) = f ′ ( ξ ) g ′ ( ξ ) \lim_{x \to x_0}\frac{f(x)}{g(x)}=\lim_{x \to x_0}\frac{f(x)-f(x_0)}{g(x)-g(x_0)}=\frac{f'(\xi)}{g'(\xi)} limx→x0g(x)f(x)=limx→x0g(x)−g(x0)f(x)−f(x0)=g′(ξ)f′(ξ)
∵ x 0 < ξ < x ∵x_0<\xi
∴ f ′ ( ξ ) g ′ ( ξ ) = lim x → x 0 f ′ ( x ) g ′ ( x ) ∴\frac{f'(\xi)}{g'(\xi)}=\lim_{x \to x_0}\frac{f'(x)}{g'(x)} ∴g′(ξ)f′(ξ)=limx→x0g′(x)f′(x)
证毕
1.4、洛必达的应用
1 、 0 0 1、\frac{0}{0} 1、00型
例1: lim x → 0 tan x − x x − sin x \lim_{x \to 0}\frac{\tan x-x}{x-\sin x} limx→0x−sinxtanx−x
【解】
lim x → 0 tan x − x x − sin x = lim x → 0 sec 2 x − 1 1 − cos x = lim x → 0 tan 2 x 1 − cos x = lim x → 0 x 2 1 2 x 2 = 2 \lim_{x \to 0}\frac{\tan x-x}{x-\sin x}=\lim_{x \to 0}\frac{\sec^2x-1}{1-\cos x}=\lim_{x \to 0}\frac{\tan^2x}{1-\cos x}=\lim_{x \to 0}\frac{x^2}{\frac{1}{2}x^2}=2 limx→0x−sinxtanx−x=limx→01−cosxsec2x−1=limx→01−cosxtan2x=limx→021x2x2=2
例2: lim x → 0 x 2 + 2 cos x − 2 ( e x − 1 ) 2 ln ( 1 + x 2 ) \lim_{x \to 0}\frac{x^2+2\cos x-2}{(e^x-1)^2\ln(1+x^2)} limx→0(ex−1)2ln(1+x2)x2+2cosx−2
【解】
注意:如果式子比较复杂,那么我们可以先化简一下再使用洛必达
化简:
lim x → 0 x 2 + 2 cos x − 2 ( e x − 1 ) 2 ln ( 1 + x 2 ) = lim x → 0 x 2 + 2 cos x − 2 x 4 \lim_{x \to 0}\frac{x^2+2\cos x-2}{(e^x-1)^2\ln(1+x^2)}=\lim_{x \to 0}\frac{x^2+2\cos x-2}{x^4} limx→0(ex−1)2ln(1+x2)x2+2cosx−2=limx→0x4x2+2cosx−2
洛必达:
lim x → 0 x 2 + 2 cos x − 2 x 4 = lim x → 0 2 x − 2 sin x 4 x 3 = 1 2 lim x → 0 1 − cos x 3 x 2 = 1 12 \lim_{x \to 0}\frac{x^2+2\cos x-2}{x^4}=\lim_{x \to 0}\frac{2x-2\sin x}{4x^3}=\frac{1}{2}\lim_{x \to 0}\frac{1-\cos x}{3x^2}=\frac{1}{12} limx→0x4x2+2cosx−2=limx→04x32x−2sinx=21limx→03x21−cosx=121
2、 ∞ ∞ \frac{∞}{∞} ∞∞
例1: lim x → + ∞ log a x x b ( a > 1 , b > 0 ) \lim_{x \to +∞}\frac{\log_a x}{x^b}(a>1,b>0) limx→+∞xblogax(a>1,b>0)
【解】
lim x → + ∞ log a x x b = lim x → + ∞ 1 x ln a b x b − 1 = 1 b ln a lim x → + ∞ 1 x b = 0 \lim_{x \to +∞}\frac{\log_a x}{x^b}=\lim_{x \to +∞}\frac{\frac{1}{x\ln a}}{b x^{b -1}}=\frac{1}{b\ln a}\lim_{x \to +∞}\frac{1}{x^b}=0 limx→+∞xblogax=limx→+∞bxb−1xlna1=blna1limx→+∞xb1=0
例2: lim x → + ∞ x b a x ( a > 1 , b > 0 ) \lim_{x \to +∞}\frac{x^b}{a^x}(a>1,b>0) limx→+∞axxb(a>1,b>0)
【解】
lim x → + ∞ b x b − 1 a x ln a \lim_{x \to +∞}\frac{bx^{b-1}}{a^x\ln a} limx→+∞axlnabxb−1此时若 b − 1 < 0 b-1<0 b−1<0,则极限为0
lim x → + ∞ b ( b − 1 ) x b − 2 a x ln a \lim_{x \to +∞}\frac{b(b-1)x^{b-2}}{a^x\ln a} limx→+∞axlnab(b−1)xb−2此时若 b − 2 < 0 b-2<0 b−2<0,则极限为0
以此类推都是一样的,则极限为0
总结:通过上述两个例子得出结论:
当 x → ∞ , a > 1 , α > 0 x\to∞,a>1,\alpha>0 x→∞,a>1,α>0时: log a x < < x α < < a x \log_ax<
3、 ∞ − ∞ ∞-∞ ∞−∞型
例1: lim x → 0 [ 1 ln ( 1 + x ) − 1 x ] \lim_{x \to 0}[\frac{1}{\ln(1+x)}-\frac{1}{x}] limx→0[ln(1+x)1−x1]
【解】
lim x → 0 [ 1 ln ( 1 + x ) − 1 x ] = lim x → 0 x − ln ( 1 + x ) x ln ( 1 + x ) \lim_{x \to 0}[\frac{1}{\ln(1+x)}-\frac{1}{x}]=\lim_{x \to 0}\frac{x-\ln(1+x)}{x\ln(1+x)} limx→0[ln(1+x)1−x1]=limx→0xln(1+x)x−ln(1+x)(此时就变成 0 0 \frac{0}{0} 00)
lim x → 0 1 − 1 1 + x 2 x = lim x → 0 x 2 x ( 1 + x ) = 1 2 \lim_{x \to 0}\frac{1-\frac{1}{1+x}}{2x}=\lim_{x \to 0}\frac{x}{2x(1+x)}=\frac{1}{2} limx→02x1−1+x1=limx→02x(1+x)x=21
4、 0 0 0^0 00型
例1: lim x → 0 + ( x ) sin x \lim_{x \to 0^+}(x)^{\sin x} limx→0+(x)sinx
【解】
( x ) sin x = e sin x ln x = e x ln x = e ln x 1 x (x)^{\sin x}=e^{\sin x\ln x}=e^{x\ln x}=e^{\frac{\ln x}{\frac{1}{x}}} (x)sinx=esinxlnx=exlnx=ex1lnx,此时指数部分就转化为了 ∞ ∞ \frac{∞}{∞} ∞∞,单独讨论指数部分最后再带入即可
lim x → 0 + ln x 1 x = lim x → 0 + 1 x − 1 x 2 = 0 \lim_{x \to 0^+}\frac{\ln x}{\frac{1}{x}}=\lim_{x \to 0^+}\frac{\frac{1}{x}}{-\frac{1}{x^2}}=0 limx→0+x1lnx=limx→0+−x21x1=0
则原式: lim x → 0 + e 0 = 1 \lim_{x \to 0^+}e^0=1 limx→0+e0=1
5、 1 ∞ 1^{∞} 1∞型
例1: lim x → + ∞ ( 2 π arctan x ) x \lim_{x \to +∞}(\frac{2}{\pi}\arctan x)^x limx→+∞(π2arctanx)x
【解】
( 2 π arctan x ) x = e x ln ( 2 π arctan x ) = e ln ( 2 π arctan x ) 1 x (\frac{2}{\pi}\arctan x)^x=e^{x\ln(\frac{2}{\pi}\arctan x)}=e^{\frac{\ln(\frac{2}{\pi}\arctan x)}{\frac{1}{x}}} (π2arctanx)x=exln(π2arctanx)=ex1ln(π2arctanx)此时指数部分就转化为了 0 0 \frac{0}{0} 00型,我们单独讨论指数部分最后代入原式即可
lim x → + ∞ ln ( 2 π arctan x ) − 1 x 2 = lim x → + ∞ 1 2 π arctan x × 2 π 1 1 + x 2 − 1 x 2 = lim x → + ∞ − 2 π 1 1 + x 2 x 2 = − 2 π \lim_{x \to +∞}\frac{\ln(\frac{2}{\pi}\arctan x)}{-\frac{1}{x^2}}=\lim_{x \to +∞}\frac{\frac{1}{\frac{2}{\pi}\arctan x}\times\frac{2}{\pi}\frac{1}{1+x^2}}{-\frac{1}{x^2}}=\lim_{x \to +∞}-\frac{2}{\pi}\frac{1}{1+x^2}x^2=-\frac{2}{\pi} limx→+∞−x21ln(π2arctanx)=limx→+∞−x21π2arctanx1×π21+x21=limx→+∞−π21+x21x2=−π2
则原式 = e − 2 π =e^{-\frac{2}{\pi}} =e−π2
总结
1.5、注意
条件: lim x → x 0 f ′ ( x ) g ′ ( x ) \lim_{x \to x_0}\frac{f'(x)}{g'(x)} limx→x0g′(x)f′(x)存在(或 ∞ ∞ ∞) ⇛ \Rrightarrow ⇛ lim x → x 0 f ( x ) g ( x ) = lim x → x 0 f ′ ( x ) g ′ ( x ) \lim_{x \to x_0}\frac{f(x)}{g(x)}=\lim_{x \to x_0}\frac{f'(x)}{g'(x)} limx→x0g(x)f(x)=limx→x0g′(x)f′(x)
上述式子就是说,如果 lim x → x 0 f ′ ( x ) g ′ ( x ) \lim_{x \to x_0}\frac{f'(x)}{g'(x)} limx→x0g′(x)f′(x)不存在,那么后面的式子就无法划等号
例: lim x → + ∞ x − sin x x + sin x \lim_{x \to +∞}\frac{x-\sin x}{x+\sin x} limx→+∞x+sinxx−sinx
洛完后: lim x → + ∞ 1 − cos x 1 + cos x ( 不存在 ) \lim_{x \to +∞}\frac{1-\cos x}{1+\cos x}(不存在) limx→+∞1+cosx1−cosx(不存在)
但洛完后不存在不代表原式不存在,因为洛完后不存在则两边不能划等号,此时就要求我们换一种方法
lim x → + ∞ x − sin x x + sin x = lim x → + ∞ 1 − sin x x 1 + sin x x = 1 \lim_{x \to +∞}\frac{x-\sin x}{x+\sin x}=\lim_{x \to +∞}\frac{1-\frac{\sin x}{x}}{1+\frac{\sin x}{x}}=1 limx→+∞x+sinxx−sinx=limx→+∞1+xsinx1−xsinx=1
2、泰勒公式
2.1、解决的问题
在微分中我们学过,如果我们需要近似的表示函数从 x 0 → Δ x + x 0 x_0 \to \Delta x+x_0 x0→Δx+x0时函数的改变量时,我们可以使用 x 0 x_0 x0这一点处的切线来近似说明
如图: y = x 2 y=x^2 y=x2与其在 x 0 = 1 2 x_0=\frac{1}{2} x0=21时的切线方程
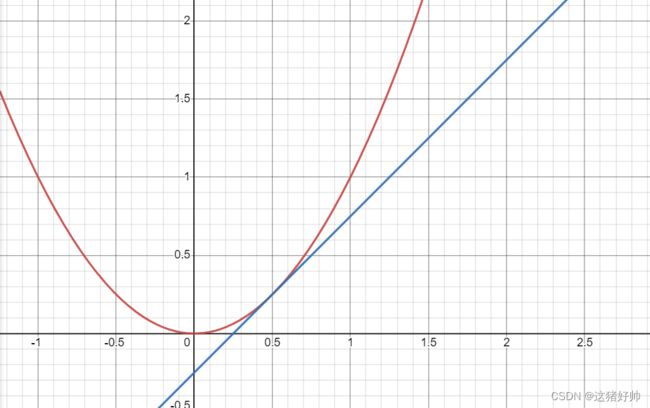
可以看到,在 x = x 0 x=x_0 x=x0的一个小领域内,它确实是非常近似的,但如果离得稍微远一点就没办法做到近似了
那么有没有什么办法能提高这个精确程度呢?
有的,我们可以通过曲线来近似说明 f ( x ) f(x) f(x)这个曲线,这也就是泰勒公式的作用
在微分中我们把函数值和一阶导数值之间建立了联系
但是如果我们需要建立函数值和高阶导致之间的联系又应该怎么办呢?这也是泰勒公式要解决的问题
2.2、引例
若 f ( x ) f(x) f(x)在 x 0 x_0 x0处可微,则
Δ y ≈ d y \Delta y\approx dy Δy≈dy
⇛ f ( x ) − f ( x 0 ) ≈ f ′ ( x 0 ) ( x − x 0 ) \Rrightarrow f(x)-f(x_0)\approx f'(x_0)(x-x_0) ⇛f(x)−f(x0)≈f′(x0)(x−x0)
⇛ f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) \Rrightarrow f(x)\approx f(x_0)+f'(x_0)(x-x_0) ⇛f(x)≈f(x0)+f′(x0)(x−x0)
结论:
f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) = P 1 ( x ) f(x)\approx f(x_0)+f'(x_0)(x-x_0)=P_1(x) f(x)≈f(x0)+f′(x0)(x−x0)=P1(x)
由可微即可导得:
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + o ( x − x 0 ) f(x)=f(x_0)+f'(x_0)(x-x_0)+o(x-x_0) f(x)=f(x0)+f′(x0)(x−x0)+o(x−x0)
这个结论的意义在于:左边是一个函数,而右边是一个一次多项式,此时在计算上多项式会较简单
但如果仅仅是一次多项式,显然当 Δ x \Delta x Δx较大时误差就会比较大,那么我们是否能用曲线(高次多项式)来表示呢?
问题:若 f ( x ) f(x) f(x)在 x 0 x_0 x0处 n n n阶可导,是否存在 n n n次多项式
P n ( x ) = a 0 + a 1 ( x − x 0 ) + a 2 ( x − x 0 ) 2 + . . . + a n ( x − x 0 ) n P_n(x)=a_0+a_1(x-x_0)+a_2(x-x_0)^2+...+a_n(x-x_0)^n Pn(x)=a0+a1(x−x0)+a2(x−x0)2+...+an(x−x0)n
使 f ( x ) = P n ( x ) + o ( ( x − x 0 ) n ) f(x)=P_n(x)+o((x-x_0)^n) f(x)=Pn(x)+o((x−x0)n)
也就是 a k ( k = 1 , 2 , 3 , . . . , n ) a_k(k={1,2,3,...,n}) ak(k=1,2,3,...,n)的值是 什么?
在我们求一次多项式 P 1 x P_1x P1x的时候,我们找的一次多项式 P 1 x P_1x P1x其实是与原函数 f ( x ) f(x) f(x)在 x 0 x_0 x0处一阶导数值相等且函数值相等的多项式
那如果我们要找一个n阶多项式 P n ( x ) P_n(x) Pn(x),那么同样的思想我们找一个n阶可导,且 P n ( k ) ( x 0 ) = f ( k ) ( x 0 ) P_n^{(k)}(x_0)=f^{(k)}(x_0) Pn(k)(x0)=f(k)(x0)的即可 ( k = 0 , 1 , 2 , 3... , n ) (k = 0,1,2,3...,n) (k=0,1,2,3...,n)
k = 0 k=0 k=0时 x = x 0 x=x_0 x=x0则 P n ( x 0 ) = a 0 P_n(x_0)=a_0 Pn(x0)=a0
k = 1 k=1 k=1时 x = x 0 x=x_0 x=x0则 P n ′ ( x 0 ) = a 1 P_n'(x_0)=a_1 Pn′(x0)=a1
k = 2 k=2 k=2时 x = x 0 x=x_0 x=x0则 P n ′ ′ ( x 0 ) = 2 ! a 2 P_n''(x_0)=2!a_2 Pn′′(x0)=2!a2则 P n ′ ′ ( x 0 ) 2 ! = f ′ ′ ( x 0 ) 2 ! = a 2 \frac{P_n''(x_0)}{2!}=\frac{f''(x_0)}{2!}=a_2 2!Pn′′(x0)=2!f′′(x0)=a2
更一般的: a k = f ( k ) ( x 0 ) k ! ( k = 0 , 1 , 2 , 3 , . . . , n ) a_k=\frac{f^{(k)}(x_0)}{k!}(k=0, 1,2,3,...,n) ak=k!f(k)(x0)(k=0,1,2,3,...,n)
2.3、内容
2.3.1、带Peano余项的泰勒公式
泰勒(Taylor)定理:设 f ( x ) f(x) f(x)在 x 0 x_0 x0处 n n n阶可微,则 f ( x ) = ∑ k = 0 n f ( k ) ( x 0 ) k ! ( x − x 0 ) k + o ( ( x − x 0 ) n ) f(x)=\sum_{k=0}^n\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k+o((x-x_0)^n) f(x)=k=0∑nk!f(k)(x0)(x−x0)k+o((x−x0)n)上式称为带Peano余项的Taylor公式,记为: P n ( x ) = ∑ k = 0 n f ( x ) ( x 0 ) k ! ( x − x 0 ) k P_n(x)=\sum_{k=0}^n\frac{f^{(x)}(x_0)}{k!}(x-x_0)k Pn(x)=k=0∑nk!f(x)(x0)(x−x0)k
f ( x ) f(x) f(x)在 x 0 x_0 x0处的 n n n次Taylor多项式 R n ( x ) = o ( ( x − x 0 ) n ) , f ( x ) 的 P e a n o 余项 R_n(x)=o((x-x_0)^n),f(x)的Peano余项 Rn(x)=o((x−x0)n),f(x)的Peano余项
带Peano余项的Taylor公式的缺点:
1、只给出余项的定性描述,不能进行定量分析
解释:在这种泰勒公式中,我们能得到的是当 x x x靠近 x 0 x_0 x0的时候,此时的误差是比 x − x 0 x-x_0 x−x0高阶的无穷小,但是有一个问题,要多靠近才算靠近呢?此时就没有一个衡量的标准
2、适用范围小
解释:在这种泰勒公式中,当 x → x 0 x \to x_0 x→x0时,只能得到 x 0 x_0 x0这个点的邻近的误差比较小,但当 x x x离 x 0 x_0 x0稍微远一点时,就无法进行估计了
于是针对上述两个缺点,人们又找到了另一种的泰勒公式,即:带Lagrange余项的泰勒公式
2.3.2、带Lagrange余项的泰勒公式
设 f ( x ) f(x) f(x)在区间 I I I中 n + 1 n+1 n+1阶可导, x 0 ∈ I x_0\in I x0∈I,则 ∀ x ∈ I , ∃ ξ ∈ I , ( ξ 在 x 0 与 x 之间 ) , \forall x \in I,\exist\xi\in I,(\xi在x_0与x之间), ∀x∈I,∃ξ∈I,(ξ在x0与x之间),使 f ( x ) = ∑ k = 0 n f ( k ) ( x 0 ) k ! ( x − x 0 ) k + f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − x 0 ) ( n + 1 ) f(x)=\sum_{k=0}^{n}\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k+\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{(n+1)} f(x)=k=0∑nk!f(k)(x0)(x−x0)k+(n+1)!f(n+1)(ξ)(x−x0)(n+1)上式称为带Lagrange余项的Taylor公式; R n ( x ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − x 0 ) n + 1 , R n ( x ) 称为 f ( x ) 的 L a g r a n g e 余项 R_n(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1} ,R_n(x)称为f(x)的Lagrange余项 Rn(x)=(n+1)!f(n+1)(ξ)(x−x0)n+1,Rn(x)称为f(x)的Lagrange余项 R n ( x ) R_n(x) Rn(x)根据有限增量公式也可以写成下面的式子: R n ( x ) = f ( n + 1 ) [ x 0 + θ ( x − x 0 ) ] ( n + 1 ) ! ( x − x 0 ) n + 1 , θ ∈ ( 0 , 1 ) R_n(x)=\frac{f^{(n+1)}[x_0+θ(x-x_0)]}{(n+1)!}(x-x_0)^{n+1},θ\in(0,1) Rn(x)=(n+1)!f(n+1)[x0+θ(x−x0)](x−x0)n+1,θ∈(0,1)
此时若 ∣ f ( n + 1 ) ( x ) ∣ ≤ M , |f^{(n+1)}(x)|\leq M, ∣f(n+1)(x)∣≤M,则 ∣ R n ( x ) ∣ = ∣ f ( n + 1 ) ( ξ ) ∣ ( n + 1 ) ! ∣ x − x 0 ∣ n + 1 ≤ M ( n + 1 ) ! ∣ x − x 0 ∣ n + 1 |R_n(x)|=\frac{|f^{(n+1)}(\xi)|}{(n+1)!}|x-x_0|^{n+1}\leq\frac{M}{(n+1)!}|x-x_0|^{n+1} ∣Rn(x)∣=(n+1)!∣f(n+1)(ξ)∣∣x−x0∣n+1≤(n+1)!M∣x−x0∣n+1
由 M M M为常数,讨论 ∣ x − x 0 ∣ n + 1 ( n + 1 ) ! , 由 lim n → ∞ a n n ! = 0 ⇛ lim n → ∞ ∣ x − x 0 ∣ n + 1 ( n + 1 ) ! = 0 \frac{|x-x_0|^{n+1}}{(n+1)!},由\lim_{n \to ∞}\frac{a^n}{n!}=0\Rrightarrow\lim_{n \to ∞}\frac{|x-x_0|^{n+1}}{(n+1)!}=0 (n+1)!∣x−x0∣n+1,由limn→∞n!an=0⇛limn→∞(n+1)!∣x−x0∣n+1=0
也就是说,此时在导函数有界的区间内,这个结果都能成立,也就都能用这个多项式代替原函数,此时产生的误差为0,适用范围就扩大了,并且由于给出了具体表达式,就可以对式子进行定量分析。
2.3.3、麦克劳林公式
若 x 0 = 0 , x_0 = 0, x0=0,则 f ( x ) = f ( 0 ) + f ′ ( 0 ) x + f ′ ′ ( 0 ) 2 ! x 2 + . . . + f ( n ) ( 0 ) n ! x n + f ( n + 1 ) ( θ x ) ( n + 1 ) ! x ( n + 1 ) f(x)=f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+...+\frac{f^{(n)}(0)}{n!}x^n+\frac{f^{(n+1)}(θx)}{(n+1)!}x^{(n+1)} f(x)=f(0)+f′(0)x+2!f′′(0)x2+...+n!f(n)(0)xn+(n+1)!f(n+1)(θx)x(n+1)
上式称为 f ( x ) f(x) f(x)的Maclaurin公式,即零点的泰勒公式
2.3.4、几个初等函数的麦克劳林公式
e x = 1 + x + x 2 2 ! + . . . + x n n ! + x ( n + 1 ) ( n + 1 ) ! e θ x e^x =1+x+\frac{x^2}{2!}+...+\frac{x^n}{n!}+\frac{x^{(n+1)}}{(n+1)!}e^{θx} ex=1+x+2!x2+...+n!xn+(n+1)!x(n+1)eθx
sin x = x − x 3 3 ! + . . . + ( − 1 ) ( m − 1 ) x 2 m − 1 ( 2 m − 1 ) ! + ( − 1 ) m cos θ x ( 2 m + 1 ) ! x 2 m + 1 \sin x = x - \frac{x^3}{3!}+...+(-1)^{(m-1)}\frac{x^{2m-1}}{(2m-1)!}+(-1)^m\frac{\cosθx}{(2m+1)!}x^{2m+1} sinx=x−3!x3+...+(−1)(m−1)(2m−1)!x2m−1+(−1)m(2m+1)!cosθxx2m+1
cos x = 1 − x 2 2 ! + . . . + ( − 1 ) m x 2 m ( 2 m ) ! + ( − 1 ) m + 1 cos θ x ( 2 m + 2 ) ! x 2 m + 2 \cos x=1-\frac{x^2}{2!}+...+(-1)^m\frac{x^{2m}}{(2m)!}+(-1)^{m+1}\frac{\cosθx}{(2m+2)!}x^{2m+2} cosx=1−2!x2+...+(−1)m(2m)!x2m+(−1)m+1(2m+2)!cosθxx2m+2
ln ( 1 + x ) = x − x 2 x + . . . + ( − 1 ) n − 1 x n n + ( − 1 ) n x n + 1 n + 1 ( 1 + θ x ) − n − 1 \ln(1+x)=x-\frac{x^2}{x}+...+(-1)^{n-1}\frac{x^n}{n}+(-1)^n\frac{x^{n+1}}{n+1}(1+θx)^{-n-1} ln(1+x)=x−xx2+...+(−1)n−1nxn+(−1)nn+1xn+1(1+θx)−n−1
( 1 + x ) α = 1 + α x + . . . + α ( α − 1 ) . . . ( α − n + 1 ) n ! x n + α ( α − 1 ) . . . ( α − n ) ( 1 + θ x ) α − n − 1 ( n + 1 ) ! x n + 1 , x ∈ ( − 1 , + ∞ ) (1+x)^\alpha=1+\alpha x+...+\frac{α(α-1)...(α-n+1)}{n!}x^n+\frac{α(α-1)...(α-n)(1+θx)^{α-n-1}}{(n+1)!}x^{n+1},x\in(-1,+∞) (1+x)α=1+αx+...+n!α(α−1)...(α−n+1)xn+(n+1)!α(α−1)...(α−n)(1+θx)α−n−1xn+1,x∈(−1,+∞)
2.4、证明
证明: f ( x ) = P n ( x ) + o ( ( x − x 0 ) n ) f(x)=P_n(x)+o((x-x_0)^n) f(x)=Pn(x)+o((x−x0)n)
即证: lim x → x 0 f ( x ) − P n ( x ) ( x − x 0 ) n = 0 \lim_{x \to x_0}\frac{f(x)-P_n(x)}{(x-x_0)^n}=0 limx→x0(x−x0)nf(x)−Pn(x)=0
lim x → x 0 f ( x ) − P n ( x ) ( x − x 0 ) n = lim x → x 0 f ′ ( x ) − P n ′ ( x ) n ( x − x 0 ) n − 1 = . . . = lim x → x 0 f ( n − 1 ) ( x ) − P n ( n − 1 ) ( x ) n ! ( x − x 0 ) \lim_{x \to x_0}\frac{f(x)-P_n(x)}{(x-x_0)^n}=\lim_{x \to x_0}\frac{f'(x)-P_n'(x)}{n(x-x_0)^{n-1}}=...=\lim_{x \to x_0}\frac{f^{(n-1)}(x)-P^{(n-1)}_n(x)}{n!(x-x_0)} limx→x0(x−x0)nf(x)−Pn(x)=limx→x0n(x−x0)n−1f′(x)−Pn′(x)=...=limx→x0n!(x−x0)f(n−1)(x)−Pn(n−1)(x)
= 1 n ! [ lim x → x 0 f ( n − 1 ) ( x ) − f ( n − 1 ) ( x 0 ) x − x 0 − lim x → x 0 P n ( n − 1 ) ( x ) − P n ( n − 1 ) ( x 0 ) x − x 0 ] =\frac{1}{n!}[\lim_{x \to x_0}\frac{f^{(n-1)}(x)-f^{(n-1)}(x_0)}{x-x_0}-\lim_{x \to x_0}\frac{P_n^{(n-1)}(x)-P_n^{(n-1)}(x_0)}{x-x_0}] =n!1[limx→x0x−x0f(n−1)(x)−f(n−1)(x0)−limx→x0x−x0Pn(n−1)(x)−Pn(n−1)(x0)]
= 1 n ! ( f ( n ) ( x 0 ) − P n ( n ) ( x 0 ) ) = 0 =\frac{1}{n!}(f^{(n)}(x_0)-P_n^{(n)}(x_0))=0 =n!1(f(n)(x0)−Pn(n)(x0))=0
证毕
2.5、泰勒公式的应用
例1:求极限 lim x → 0 cos x − e − x 2 2 x 4 \lim_{x \to 0}\frac{\cos x-e^{-\frac{x^2}{2}}}{x^4} limx→0x4cosx−e−2x2
【解】
由于 x 4 x^4 x4,所以我们只写到四次项即可
cos x = 1 − x 2 2 ! + x 4 4 ! + o ( x 4 ) \cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}+o(x^4) cosx=1−2!x2+4!x4+o(x4)
e − x 2 2 = 1 − x 2 2 + 1 2 ! ( − x 2 2 ) + o ( x 4 ) e^{-\frac{x^2}{2}}=1-\frac{x^2}{2}+\frac{1}{2!}(-\frac{x^2}{2})+o(x^4) e−2x2=1−2x2+2!1(−2x2)+o(x4)
原式= lim x → 0 − 1 12 x 4 x 4 = − 1 12 \lim_{x \to 0}\frac{-\frac{1}{12}x^4}{x^4}=-\frac{1}{12} limx→0x4−121x4=−121
例2:设 f ′ ′ ( x ) > 0 f''(x)>0 f′′(x)>0,当 x → 0 x \to 0 x→0时, f ( x ) f(x) f(x)与 x x x是等价无穷小,证明:当 x ≠ 0 x ≠ 0 x=0时, f ( x ) > x f(x)>x f(x)>x
【解】
∵ lim x → 0 f ( x ) x = 1 ⇛ f ( 0 ) = 0 , f ′ ( 0 ) = 1 ∵\lim_{x \to 0}\frac{f(x)}{x}=1\Rrightarrow f(0)=0,f'(0)=1 ∵limx→0xf(x)=1⇛f(0)=0,f′(0)=1
∴ f ( x ) = f ( 0 ) + f ′ ( 0 ) x + f ′ ′ ( ξ ) 2 ! x 2 = x + f ′ ′ ( ξ ) 2 ! x 2 > x ∴f(x)=f(0)+f'(0)x+\frac{f''(\xi)}{2!}x^2=x+\frac{f''(\xi)}{2!}x^2>x ∴f(x)=f(0)+f′(0)x+2!f′′(ξ)x2=x+2!f′′(ξ)x2>x
∴ f ( x ) > x ∴f(x)>x ∴f(x)>x
2.6、总结
泰勒公式的本质是:
1、用多项式来逼近 f ( x ) f(x) f(x)
2、用已知点的信息表示未知点
两种泰勒公式分别什么时候用呢?
1、由于Peano余项泰勒公式表示的是一个点及其邻域内的形态
故当求极限/极值时可以使用Peano余项的泰勒公式
2、Largrange余项泰勒公式表示的是一个整体的思想,故当求最值/证明不等式时可以用Largrange余项泰勒公式
3、函数的单调性
3.1、函数单调性的判别方法
定理:设函数 f ( x ) f(x) f(x)在区间 [ a , b ] [a,b] [a,b]上连续,在 ( a , b ) (a,b) (a,b)内可导,则
1、如果在 ( a , b ) (a,b) (a,b)内 f ′ ( x ) ≥ 0 f'(x)\geq0 f′(x)≥0,且等号只在有限个点上成立,则 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]上单调增加;
2、如果在 ( a , b ) (a,b) (a,b)内 f ′ ( x ) ≤ 0 f'(x)\leq0 f′(x)≤0,且等号只在有限个点上成立,则 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]上单调减少;
3.2、证明
证: f ′ ( x ) > 0 , x 2 > x 1 时 f ( x 2 ) > f ( x 1 ) f'(x) > 0,x_2>x_1时f(x_2)>f(x_1) f′(x)>0,x2>x1时f(x2)>f(x1)
即证: f ( x 2 ) − f ( x 1 ) > 0 f(x_2)-f(x_1)>0 f(x2)−f(x1)>0
f ( x 2 ) − f ( x 1 ) = f ′ ( ξ ) ( x 2 − x 1 ) > 0 f(x_2)-f(x_1)=f'(\xi)(x_2-x_1)>0 f(x2)−f(x1)=f′(ξ)(x2−x1)>0
若 f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0
则把区间 ( a , b ) (a,b) (a,b)分为 [ a , x 0 ] [a,x_0] [a,x0]与 [ x 0 , b ] [x_0,b] [x0,b]
此时两个区间同单调
其余有限个 f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0也同理
证毕
3.3、应用
例:确定 f ( x ) = e x − x − 1 f(x)=e^x-x-1 f(x)=ex−x−1的增减区间
【解】
f ′ ( x ) = e x − 1 f'(x)=e^x-1 f′(x)=ex−1
令 e x − 1 = 0 , x = 0 e^x-1=0,x=0 ex−1=0,x=0
x ∈ ( − ∞ , 0 ) 时 f ′ ( x ) < 0 ⇛ f ( x ) x\in(-∞,0)时f'(x)<0\Rrightarrow f(x) x∈(−∞,0)时f′(x)<0⇛f(x)单减
x ∈ ( 0 , + ∞ ) 时 f ′ ( x ) > 0 ⇛ f ( x ) x \in(0,+∞)时f'(x)>0\Rrightarrow f(x) x∈(0,+∞)时f′(x)>0⇛f(x)单增
例:证 x > 0 x>0 x>0时 , x − x 3 6 < sin x < x ,x-\frac{x^3}{6}<\sin x
【解】
①证: x > 0 , x > sin x x>0,x>\sin x x>0,x>sinx
即证: f ( x ) = x − sin x > 0 f(x)=x-\sin x >0 f(x)=x−sinx>0
f ′ ( x ) = 1 − cos x ≥ 0 f'(x)=1-\cos x\geq0 f′(x)=1−cosx≥0
∴ x > sin x ∴x>\sin x ∴x>sinx
②证: x > 0 , sin x > x − x 3 6 x>0,\sin x>x-\frac{x^3}{6} x>0,sinx>x−6x3
即证: g ( x ) = sin x − x + x 3 6 > 0 g(x)=\sin x-x+\frac{x^3}{6}>0 g(x)=sinx−x+6x3>0
g ′ ( x ) = cos x − 1 + 1 2 x 2 g'(x)=\cos x-1+\frac{1}{2}x^2 g′(x)=cosx−1+21x2
g ′ ′ ( x ) = x − sin x g''(x)=x-\sin x g′′(x)=x−sinx
由①得: x − sin x > 0 x-\sin x>0 x−sinx>0
∴ g ′ ( x ) ∴g'(x) ∴g′(x)单增
∵ g ( 0 ) = 0 ∵g(0)=0 ∵g(0)=0
∴ x > 0 , g ( x ) > 0 ∴x>0,g(x)>0 ∴x>0,g(x)>0
由①②证毕
4、曲线的凹凸性与拐点
4.1、定义
定义:设函数 f ( x ) f(x) f(x)在区间 I I I上连续,如果对 I I I上任意两点 x 1 , x 2 x_1,x_2 x1,x2恒有 f ( x 1 + x 2 2 ) < f ( x 1 ) + f ( x 2 ) 2 f(\frac{x_1+x_2}{2})<\frac{f(x_1)+f(x_2)}{2} f(2x1+x2)<2f(x1)+f(x2)
则称 f ( x ) f(x) f(x)在 I I I上的图形是凹的,如果恒有 f ( x 1 + x 2 2 ) > f ( x 1 ) + f ( x 2 ) 2 f(\frac{x_1+x_2}{2})>\frac{f(x_1)+f(x_2)}{2} f(2x1+x2)>2f(x1)+f(x2)则称 f ( x ) f(x) f(x)在 I I I上的图形是凸的
如图:凹函数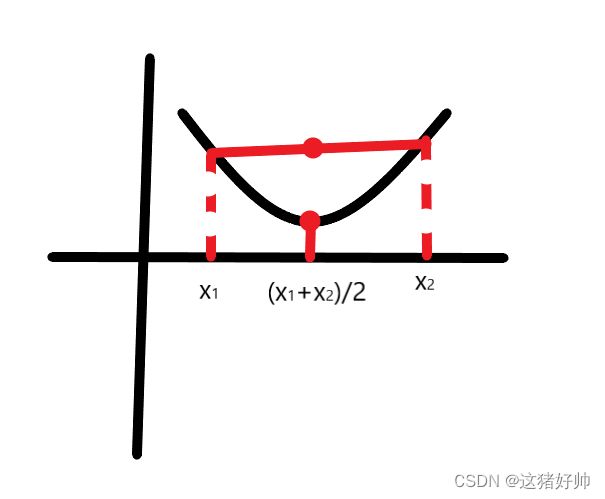
上图中,每一点 ( x 0 , f ( x 0 ) ) (x_0,f(x_0)) (x0,f(x0))都能作出切线,并且它的切线是逆时针方向旋转的,即斜率是递增的,那么 f ′ ( x ) f'(x) f′(x)单增, f ′ ′ ( x ) > 0 f''(x)>0 f′′(x)>0
如图凸函数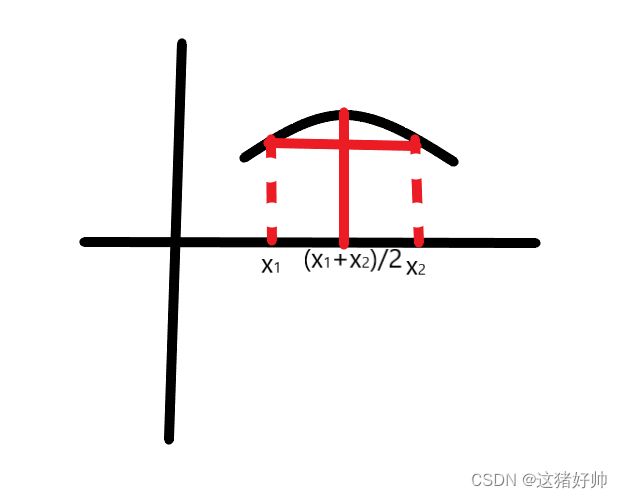
上图中,每一点 ( x 0 , f ( x 0 ) ) (x_0,f(x_0)) (x0,f(x0))都能作出切线,并且它的切线是顺时针方向旋转的,即斜率是递减的,那么 f ′ ( x ) f'(x) f′(x)单减, f ′ ′ ( x ) < 0 f''(x)<0 f′′(x)<0
就可以得到以下结论
定理:设函数 f ( x ) f(x) f(x)在区间 [ a , b ] [a,b] [a,b]上连续,在 ( a , b ) (a,b) (a,b)内二阶可导,
1、若在 ( a , b ) (a,b) (a,b)内 f ′ ′ ( x ) > 0 , f''(x)>0, f′′(x)>0,则 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]上的图形是凹的
2、若在 ( a , b ) (a,b) (a,b)内 f ′ ′ ( x ) < 0 , f''(x)<0, f′′(x)<0,则 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]上的图形是凸的
4.2、证明
若 f ′ ′ ( x ) > 0 , f''(x)>0, f′′(x)>0,则 f ( x ) f(x) f(x)是凹的
【证】
假设 x 1 < x 2 x_1
根据定义: f ( x 1 + x 2 2 ) < f ( x 1 ) + f ( x 2 ) 2 f(\frac{x_1+x_2}{2})<\frac{f(x_1)+f(x_2)}{2} f(2x1+x2)<2f(x1)+f(x2)
令 x 1 + x 2 2 = x 0 \frac{x_1+x_2}{2}=x_0 2x1+x2=x0
即证明 f ( x 1 ) + f ( x 2 ) − 2 f ( x 0 ) > 0 f(x_1)+f(x_2)-2f(x_0)>0 f(x1)+f(x2)−2f(x0)>0
[ f ( x 2 ) − f ( x 0 ) ] − [ f ( x 0 ) − f ( x 1 ) ] [f(x_2)-f(x_0)]-[f(x_0)-f(x_1)] [f(x2)−f(x0)]−[f(x0)−f(x1)]
= f ′ ( ξ 1 ) ( x 2 − x 0 ) − f ′ ( ξ 2 ) ( x 0 − x 1 ) =f'(\xi_1)(x_2-x_0)-f'(\xi_2)(x_0-x_1) =f′(ξ1)(x2−x0)−f′(ξ2)(x0−x1)
= x 2 − x 1 2 [ f ′ ( ξ 1 ) − f ′ ( ξ 2 ) ] =\frac{x_2-x_1}{2}[f'(\xi_1)-f'(\xi_2)] =2x2−x1[f′(ξ1)−f′(ξ2)]
由 x 1 < x 2 , f ′ ′ ( x ) > 0 x_1
即 x 2 − x 1 2 [ f ′ ( ξ 1 ) − f ′ ( ξ 2 ) ] > 0 \frac{x_2-x_1}{2}[f'(\xi_1)-f'(\xi_2)]>0 2x2−x1[f′(ξ1)−f′(ξ2)]>0
证毕
4.3、拐点
拐点即函数凹凸性变化的点,即二阶导数异号的点
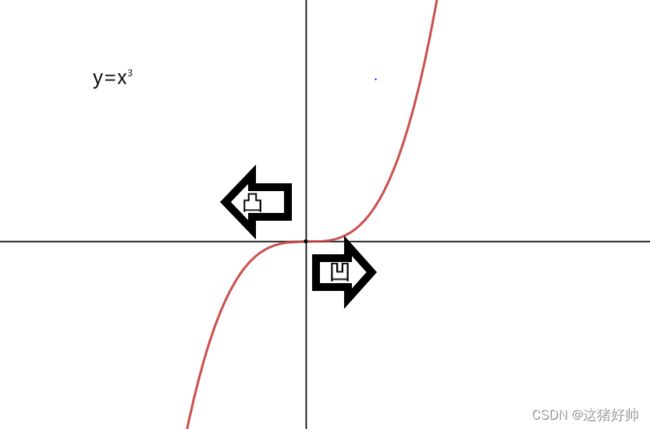
如图,(0,0)点即为 y = x 3 y=x^3 y=x3的拐点
拐点的二阶导数如果存在,则二阶导数一定为0
但二阶导数为0的点不一定是拐点,例如 f ( x ) = x 4 f(x)=x^4 f(x)=x4
二阶导数不存在的点也有可能是拐点。例如: f ( x ) = x 1 3 f(x)=x^{\frac{1}{3}} f(x)=x31
5、函数的极值和最值
5.1、极值
极值定义:若 ∃ δ > 0 , \exist\delta >0, ∃δ>0,使得
∀ x ∈ U ( x 0 , δ ) \forall x\in U(x_0,\delta) ∀x∈U(x0,δ)恒有 f ( x ) ≥ f ( x 0 ) , f(x)\geq f(x_0), f(x)≥f(x0),则称 f ( x ) f(x) f(x)在 x 0 x_0 x0取极小值
∀ x ∈ U ( x 0 , δ ) \forall x\in U(x_0,\delta) ∀x∈U(x0,δ)恒有 f ( x ) ≤ f ( x 0 ) , f(x)\leq f(x_0), f(x)≤f(x0),则称 f ( x ) f(x) f(x)在 x 0 x_0 x0取极大值
极值的必要条件:若 f ( x ) f(x) f(x)在 x 0 x_0 x0处可导,且在 x 0 x_0 x0取得极值,则 f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0
数学中,我们把导数为0的点称为驻点
注意:
1、驻点不一定是极值点,例如: f ( x ) = x 3 f(x)=x^3 f(x)=x3
2、极值点不一定是驻点,例如: f ( x ) = ∣ x ∣ f(x)=|x| f(x)=∣x∣
3、若 f ( x ) f(x) f(x)可导,则它的极值点一定是驻点
可能取得极值点:
1、 f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0
2、 f ′ ( x 0 ) f'(x_0) f′(x0)不存在
极值的第一充分条件:
设 f ( x ) f(x) f(x)在 U ˚ ( x 0 , δ ) \mathring U(x_0,\delta) U˚(x0,δ)内可导,且 f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0(若 f ′ ( x ) 不存在则 f ( x ) f'(x)不存在则f(x) f′(x)不存在则f(x)在 x 0 x_0 x0处连续即可)
1、若 x < x 0 x < x_0 x<x0时, f ′ ( x ) ≥ 0 ; x > x 0 f'(x)\geq 0;x>x_0 f′(x)≥0;x>x0时, f ′ ( x ) ≤ 0 , f'(x)\leq0, f′(x)≤0,则 f f f在 x 0 x_0 x0处取得极大值
2、若 x < x 0 x < x_0 x<x0时, f ′ ( x ) ≤ 0 ; x > x 0 f'(x)\leq 0;x>x_0 f′(x)≤0;x>x0时, f ′ ( x ) ≥ 0 , f'(x)\geq0, f′(x)≥0,则 f f f在 x 0 x_0 x0处取得极小值
3、若 f ′ ( x ) f'(x) f′(x)在 x 0 x_0 x0的两侧不变号,则 f f f在 x 0 x_0 x0无极值
极值的第二充分条件:
设 f ′ ( x 0 ) = 0 , f ′ ′ ( x 0 ) ≠ 0 f'(x_0)=0,f''(x_0)≠0 f′(x0)=0,f′′(x0)=0
1、当 f ′ ′ ( x 0 ) < 0 , f ( x ) f''(x_0)<0,f(x) f′′(x0)<0,f(x)在 x 0 x_0 x0处取极大值
2、当 f ′ ( x 0 ) > 0 , f ( x ) f'(x_0)>0,f(x) f′(x0)>0,f(x)在 x 0 x_0 x0处取极小值
5.2、最大值与最小值问题
1、求连续函数 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]上的最值
第一步:求出 f ( x ) f(x) f(x)在 ( a , b ) (a,b) (a,b)内的驻点和不可导点
第二步:把第一步求出的所有点以及端点代入函数值
第三步:比较以上各点函数值
6、曲线的渐近线
1、若 lim x → − ∞ f ( x ) = A 或 lim x → + ∞ f ( x ) = A \lim_{x \to -∞}f(x)=A或\lim_{x \to +∞}f(x)=A limx→−∞f(x)=A或limx→+∞f(x)=A那么 y = A y=A y=A是曲线 y = f ( x ) y=f(x) y=f(x)的水平渐近线
qu
2、若 lim x → x 0 f ( x ) = ∞ , \lim_{x \to x_0}f(x)=∞, limx→x0f(x)=∞,那么 x = x 0 x = x_0 x=x0是 y = f ( x ) y=f(x) y=f(x)的垂直渐近线
3、若 lim x → ∞ f ( x ) x = a , b = lim x → ∞ ( f ( x ) − a x ) , \lim_{x\to∞}\frac{f(x)}{x}=a,b=\lim_{x\to ∞}(f(x)-ax), limx→∞xf(x)=a,b=limx→∞(f(x)−ax),那么 y = a x + b y=ax+b y=ax+b是 y = f ( x ) y=f(x) y=f(x)的斜渐近线
7.函数图像的描绘
步骤:
1、确定函数 y = f ( x ) y=f(x) y=f(x)的定义域,并考察其奇偶性及周期性
2、求 f ′ ( x ) , f ′ ′ ( x ) , f'(x),f''(x), f′(x),f′′(x),并求出 f ′ ( x ) f'(x) f′(x)及 f ′ ′ ( x ) f''(x) f′′(x)为0或不存在的点
3、判别增减及凹凸区间,求出极值和拐点
4、求渐近线
5、确定某些特殊点,描绘函数图形
8、曲率
8.1、弧微分
8.1.1、弧微分推导
设 y = f ( x ) y=f(x) y=f(x)在 ( a , b ) (a,b) (a,b)内有连续导数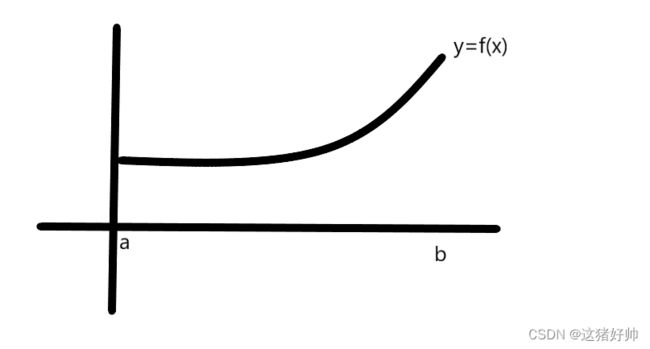
在 f ( x ) f(x) f(x)图像上任意取一个起点 M 0 ( x 0 , f ( x 0 ) ) M_0(x_0,f(x_0)) M0(x0,f(x0))

此时任给 x x x,对应曲线上的点为 M ( x , f ( x ) ) M(x,f(x)) M(x,f(x))
若 x > x 0 x>x_0 x>x0,则从 M 0 M_0 M0到 M M M的弧长为正
若 x < x 0 x
此时我们取 x > x 0 x > x_0 x>x0

弧长函数: S = S ( x ) = ∣ M 0 M ⌢ ∣ , ( x > x 0 ) S=S(x)=|\mathop{M_0M}\limits^{\frown}|,(x>x_0) S=S(x)=∣M0M⌢∣,(x>x0)
那么很明显弧长函数递增的, S > 0 , S ′ ( x ) > 0 S>0,S'(x)>0 S>0,S′(x)>0
而弧微分就是弧长函数的微分
那么我们首先研究它的导数
取一点 M ′ ( x + Δ x , f ( x + Δ x ) ) M'(x+\Delta x,f(x+\Delta x)) M′(x+Δx,f(x+Δx))
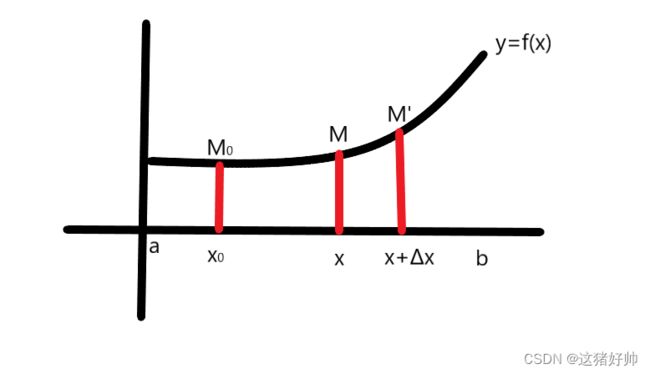
此时对 x x x的导数即为: lim Δ x → 0 Δ s Δ x \lim_{\Delta x \to 0}\frac{\Delta s}{\Delta x} limΔx→0ΔxΔs
( Δ s Δ x ) 2 = ( ∣ M M ′ ⌢ ∣ Δ x ) 2 (\frac{\Delta s}{\Delta x})^2=(\frac{|\mathop{MM'}\limits^{\frown}|}{\Delta x})^2 (ΔxΔs)2=(Δx∣MM′⌢∣)2
此时我们连接 M M ′ , MM', MM′,取得一条弦 ∣ M M ′ ∣ ‾ \overline{|MM'|} ∣MM′∣,如图
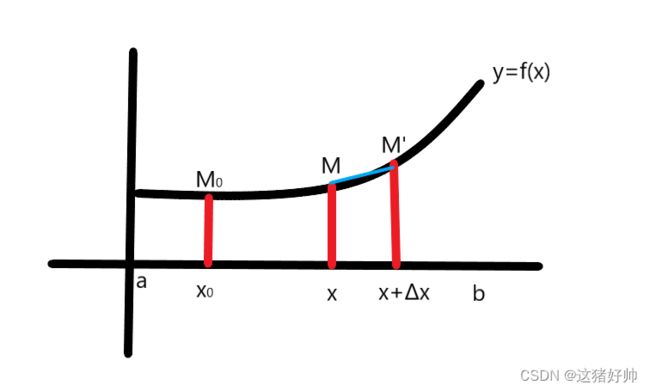
∴ d s d x = ( ∣ M M ′ ⌢ ∣ Δ x ) 2 = ( ∣ M M ′ ⌢ ∣ ∣ M M ′ ∣ ‾ ) 2 ( ∣ M M ′ ∣ ‾ Δ x ) 2 ∴\frac{ds}{dx}=(\frac{|\mathop{MM'}\limits^{\frown}|}{\Delta x})^2=(\frac{|\mathop{MM'}\limits^{\frown}|}{\overline{|MM'|}})^2(\frac{\overline{|MM'|}}{\Delta x})^2 ∴dxds=(Δx∣MM′⌢∣)2=(∣MM′∣∣MM′⌢∣)2(Δx∣MM′∣)2
∣ M M ′ ∣ ‾ = ( Δ x ) 2 + ( Δ y ) 2 \overline{|MM'|}=(\Delta x)^2+(\Delta y)^2 ∣MM′∣=(Δx)2+(Δy)2
∴ ( ∣ M M ′ ⌢ ∣ ∣ M M ′ ∣ ‾ ) 2 ( ∣ M M ′ ∣ ‾ Δ x ) 2 = ( ∣ M M ′ ⌢ ∣ ∣ M M ′ ∣ ‾ ) 2 [ 1 + ( Δ y Δ x ) 2 ] ∴(\frac{|\mathop{MM'}\limits^{\frown}|}{\overline{|MM'|}})^2(\frac{\overline{|MM'|}}{\Delta x})^2=(\frac{|\mathop{MM'}\limits^{\frown}|}{\overline{|MM'|}})^2[1+(\frac{\Delta y}{\Delta x})^2] ∴(∣MM′∣∣MM′⌢∣)2(Δx∣MM′∣)2=(∣MM′∣∣MM′⌢∣)2[1+(ΔxΔy)2]
而当 Δ x → 0 \Delta x\to 0 Δx→0时, M ′ → M M'\to M M′→M, ∣ M M ′ ⌢ ∣ ∣ M M ′ ∣ ‾ = 1 , \frac{|\mathop{MM'}\limits^{\frown}|}{\overline{|MM'|}}=1, ∣MM′∣∣MM′⌢∣=1,所以上式还能写成:
lim Δ x → 0 ( ∣ M M ′ ⌢ ∣ Δ x ) 2 = 1 + ( y ′ ) 2 \lim_{\Delta x \to 0}(\frac{|\mathop{MM'}\limits^{\frown}|}{\Delta x})^2=1+(y')^2 limΔx→0(Δx∣MM′⌢∣)2=1+(y′)2
lim Δ x → 0 ∣ M M ′ ⌢ ∣ Δ x = 1 + ( y ′ ) 2 \lim_{\Delta x \to 0}\frac{|\mathop{MM'}\limits^{\frown}|}{\Delta x}=\sqrt{1+(y')^2} limΔx→0Δx∣MM′⌢∣=1+(y′)2
d s = 1 + ( y ′ ) 2 d x = ( d x ) 2 + ( d y ) 2 , ds=\sqrt{1+(y')^2}dx=\sqrt{(dx)^2+(dy)^2}, ds=1+(y′)2dx=(dx)2+(dy)2,这也就是弧微分公式
而 s ′ ( x ) = 1 + ( y ′ ) 2 s'(x)=\sqrt{1+(y')^2} s′(x)=1+(y′)2