一元线性回归（Simple Linear Regression）

简单线性回归（Simple Linear Regression）简介

简单线性回归 Simple Linear Regression（一元线性回归）：

• 又称为一元线性回归，是一种统计分析方法，用于研究一个因变量和一个自变量之间的线性关系。

• 一元线性回归模型通常表示为 y = a*x + b，其中a是斜率，b是截距。其表示的含义是，自变量x每增加一个单位，因变量y平均增加a个单位。

• 一元线性回归是一种强大的统计分析工具，可以用来探索和理解两个变量之间的线性关系。然而，对于非线性关系或其他更复杂的关系时就不适用了，需要其他更复杂的模型，如多元线性回归，逻辑回归，等等。

理解数据

这里我们使用了加拿大政府公开数据中的油耗数据集，其中包含特定型号的油耗评级和在加拿大零售的新轻型车辆的估计二氧化碳排放量

• MODELYEAR 2014
• MAKE Acura
• MODEL ILX
• VEHICLE CLASS SUV
• ENGINE SIZE 引擎尺寸
• CYLINDERS 气缸
• TRANSMISSION 传动
• FUEL CONSUMPTION in CITY(L/100 km) 油耗城市
• FUEL CONSUMPTION in HWY (L/100 km) 油耗高速公路
• FUEL CONSUMPTION COMB (L/100 km) 综合油耗
• CO2 EMISSIONS (g/km) 二氧化碳排放量

数据处理

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
%matplotlib inline

读取数据

# 使用pandas直接读取文件，会得到一个dataframe格式的数据表
df = pd.read_csv("FuelConsumptionCo2.csv")

数据预览

这里使用到head()函数，默认值为显示前5行数据，可以在括号中输入不同的数值来输出显示需要的数据行数。

# 预览数据
df.head()

数据探索

数据统计信息

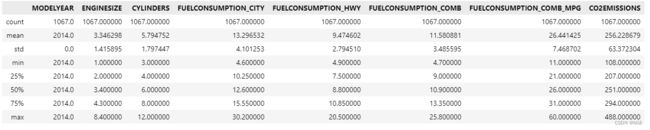
使用describe()函数，可以直接看每一列数据的一些统计数据，如count（计数），mean（均值），std（方差），min（最小值），max（最大值），还有四分位数等。

# 可以先观察整体的数据情况。
df.describe()

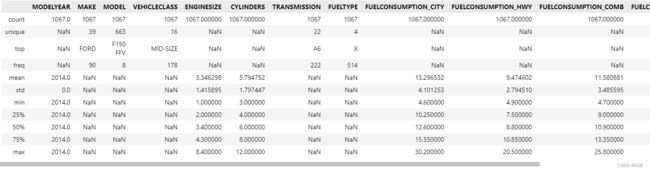
调用describe()函数时，在括号内添加 include='all'，还会显示更多的数据统计信息。

df.describe(include='all')

数据类型

使用df.info()函数，可以查看全部数据的数据类型和缺失值信息，方便我们后续分析数据时，能够挑选合适的数据类型。

df.info()

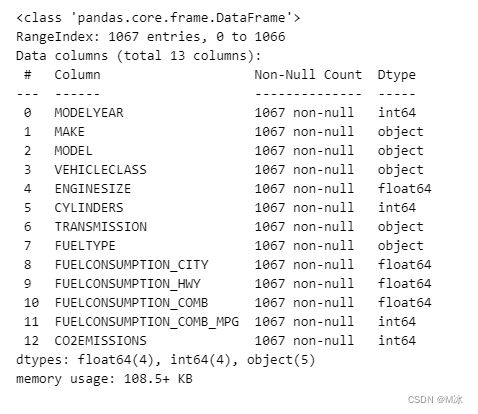
通过上面结果，可以看到此数据集共1067行数据，并且每一列数据都没有空值的情况。
并且 MODELYEAR, ENGINESIZE, CYLINDERS, FUELCONSUMPTION_CITY, FUELCONSUMPTION_HWY, FUELCONSUMPTION_COMB, FUELCONSUMPTION_COMB_MPG, CO2EMISSIONS 这7个变量为数值型变量

MAKE, MODEL, VEHICLECLASS, TRANSMISSION, FUELTYPE, 这5个变量为非数值型变量。

由于我们这次是介绍简单线性回归，所以用不到非数值型变量，下面我们对数据中的变量进行选择。

这里我们挑选了 ENGINESIZE，FUELCONSUMPTION_COMB，两个变量和结果数据CO2EMISSIONS。

df = df[['CO2EMISSIONS','ENGINESIZE','FUELCONSUMPTION_COMB']]

查看数据的直方图

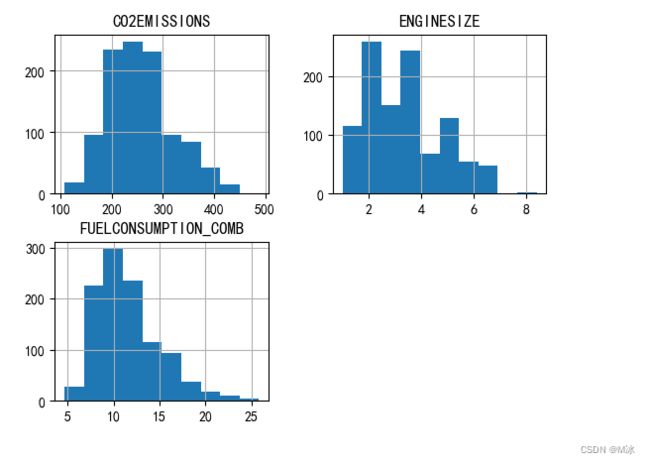
通过直方图来观察不同数据的分布情况。
这里我们直接用hist()函数来生成数据的直方图

df.hist()
plt.show()

通过散点图查看数据的相关关系

通过绘制 ENGINESIZE, 于 CO2EMISSIONS，的散点图来观察他们之间有没有相关关系

sns.scatterplot(data=df[['CO2EMISSIONS','FUELCONSUMPTION_COMB']],x='CO2EMISSIONS',y='FUELCONSUMPTION_COMB')
plt.show()

可以看出这他们之间有明显的正相关关系。

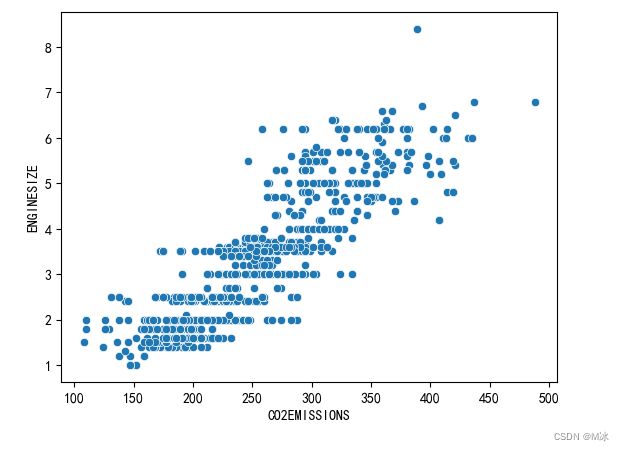
FUELCONSUMPTION_COMB于 CO2EMISSIONS,的散点图来观察他们之间有没有相关关系

sns.scatterplot(data=df[['CO2EMISSIONS','ENGINESIZE']],x='CO2EMISSIONS',y='ENGINESIZE')
plt.show()

• 这幅图同样也能看出这他们之间有明显的正相关关系。

相关系数

前面通过观察图形，可以了解两个数据之间有没有相关关系，是正相关还是负相关等。
那么如果我们要想知道他们之间的相关性到底有多强，具体的数值是多少，这就需要通过计算相关系数来得到了。

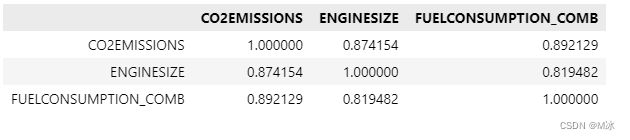
通过函数corr()来计算数据之间的相关系数。

df.corr()

• 从相关系数值可以看到，FUELCONSUMPTION_COMB于CO2EMISSIONS的相关性为0.892129 比 ENGINESIZE于CO2EMISSIONS的相关性要高一些。
• 那么我们可以认为FUELCONSUMPTION_COMB 的大小对二氧化碳排放的影响要大于 ENGINESIZE 对二氧化碳排放量的影响

建立模型

通过前面的分析，我们选择相关性更高的 FUELCONSUMPTION_COMB 来建立于CO2EMISSIONS 的线性回归模型。

创建训练数据和测试数据

把数据处理完后，我们将数据集拆分为训练集和测试集。一般来说用 80% 的数据用来训练，20% 的数据用来测试。这样能够保证有足够的数据来训练模型，并且也有一定的数据用来检测模型的拟合效果。

这里我们用到sklearn中的数据分割函数train_test_split来实现训练数据与测试数据的分割。

# 导入数据分割函数
from sklearn.model_selection import train_test_split

先拆分自变量 X，与因变量 y，由于是建立简单线性回归，只需要一个自变量，所以自变量只需要选择一列数据。

# 拆分自变量X与因变量y
y = df[['CO2EMISSIONS']]
X = df[['ENGINESIZE']]

自变量 X 和因变量 y 设置好后，就可以进行训练数据和测试数据的分割了。

# 拆分训练数据与测试数据
X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.2, random_state=4)
print ('Train set:', X_train.shape,  y_train.shape)
print ('Test set:', X_test.shape,  y_test.shape)

建立简单线性回归模型

from sklearn import linear_model

regr = linear_model.LinearRegression()
regr.fit(X_train, y_train)

查看回归方程阐述

当模型训练完成之后，可以通过coef_，intercept_这两个函数来获取回归方程中的截距和回归系数

print ('Coefficients 系数: ', regr.coef_)
print ('Intercept 截距: ',regr.intercept_)

绘制拟合图

得到截距和回归系数之后，我们可以根据得到的数值来绘制拟合图。

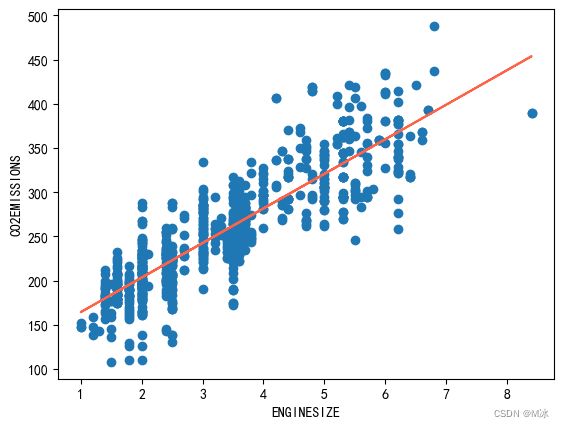
plt.scatter(X_train, y_train)
plt.plot(X_train, regr.coef_*X_train + regr.intercept_, 'tomato')
plt.xlabel("ENGINESIZE")
plt.ylabel("CO2EMISSIONS")
plt.show()

• 根据拟合图可以看出，拟合效果还是可以的。

• 至于模型的效果到底是好还是坏，还需要对模型进行评估。

模型评估

我们通过比较实际值和预测值来计算回归模型的准确性。评估指标在模型开发中起着关键作用，因为他提供了可供参考的具体数值，能够很明确的知道模型的差距。

评估指标：

• MAE是平均绝对误差（Mean Absolute Error）：它是一种用于评估预测模型性能的指标，主要衡量预测值与真实值之间的绝对差异。通常，MAE越小，预测模型的性能越好。与MSE相比，MAE不考虑误差的方向，只考虑了误差的大小。因此，在某些情况下，MAE可能会比MSE更好地描述模型的性能。

• MSE是均方误差（Mean Squared Error）：它是一种用于评估预测模型性能的指标，主要衡量预测值与真实值之间的差异。通常，MSE越小，预测模型的性能越好。

• RMSE均方根误差（Root Mean Squared Error)：MSE的平方根称为均方根误差（RMSE），它与MSE的意义相似，但是更容易解释。RMSE表示预测值与真实值之间的平均误差，也是评估预测模型性能的重要指标之一。

• R-squared （$R^2$）：R 平方不是误差，而是衡量回归模型性能的常用指标。它表示数据点与拟合回归线的接近程度。R 平方值越高，模型对数据的拟合越好。（取值范围在0~1之间）

这里我们选用 MAE，RMSE，$R^2$ 三个评估指标来对模型进行评估。

from sklearn.metrics import r2_score

y_test_ = regr.predict(X_test)

MAE = np.mean(np.absolute(y_test_ - y_test))
RMSE = np.sqrt(np.mean((y_test_ - y_test) ** 2))
R2 = r2_score(y_test , y_test_) 

print("MAE  : %.3f" % MAE)
print("RMSE : %.3f" % RMSE)
print("R2   : %.3f" % R2)

因为MAE，和 RMSE 都是误差值，虽然是越小越好，但是到底应该多小才算好并没有具体的概念，这里我们可以通过计算 MAE 和 RMSE 在真实
值中的比重，就能够有一个具体的概念，并且在得到预测结果也能够有一个误差的比重范围。

MAE_rate = round(MAE/y_test.mean()*100,2)
RMSE_rate = round(RMSE/y_test.mean()*100,2)

print("MAE  : {}%".format(MAE_rate[0]) )
print("RMSE : {}%".format(RMSE_rate[0]))

根据模型的评分可得出：

• $R^2$的得分为0.8149，表示模型的拟合效果已经很高了，再实际工作中，能够达到0.8就已经可以投入生产环境使用了。
• MAE和RMSE的数值都比较低，基本在10%的范围，也就是说，用模型预测出来的值与真实值之间的误差在-10% ~ +10% 的范围内。

使用模型进行预测

当完成了模型的训练，就可以用训练好的模型进行数据的预测了。

预测时直接调用训练好的模型，并使用predict()函数就能够得到一个或者一组预测的结果

预测一组数据的时候，建立一个数组，传入需要进行预测的数值，如下，我们预测引擎尺寸ENGINESIZE为 4，5，6 时，二氧化碳排放量为多少。

predict = pd.DataFrame({
    'ENGINESIZE':[4,5,6]
})

regr.predict(predict)

输出的结果是一个与输入参数对应的数组：
当ENGINESIZE = 4 时，二氧化碳排放量为281.61452375，
当ENGINESIZE = 5时，二氧化碳排放量为320.73146074，
当ENGINESIZE = 6时，二氧化碳排放量为359.84839774.

数据集下载：

• 使用的数据为 加拿大政府公开数据 可以根据需要进行下载