数据结构与算法XS班-左程云第八节课笔记(归并排序和快速排序)
第8节 归并排序和快速排序
##这是数据结构与算法新手班-左程云第八节课的笔记##
归并排序
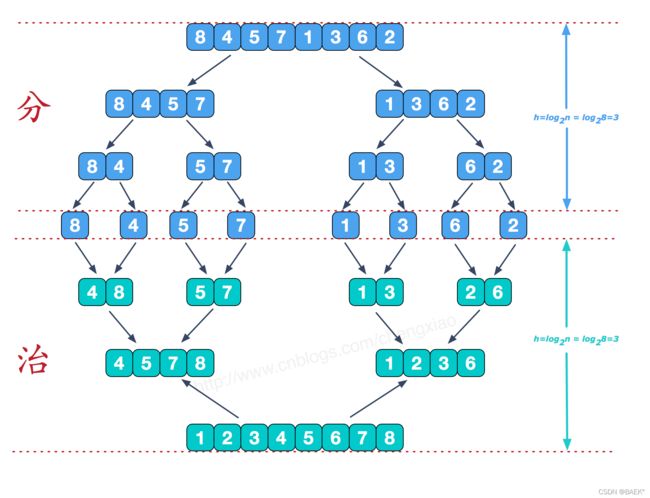
归并排序实际上是一个很经典的排序方法,时间复杂度o(N*logN)。
- 递归版本(图解排序算法(四)之归并排序 - dreamcatcher-cx - 博客园 (cnblogs.com))
package class08;
public class Code02_MergeSort {
// 递归方法实现
public static void mergeSort1(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
process(arr, 0, arr.length - 1);
}
// arr[L...R]范围上,请让这个范围上的数,有序!
public static void process(int[] arr, int L, int R) {
// 只有一个数字不需要排序,base case
if (L == R) {
return;
}
// int mid = (L + R) / 2
int mid = L + ((R - L) >> 1);
// 左有序
process(arr, L, mid);
// 右有序
process(arr, mid + 1, R);
// 一起有序
merge(arr, L, mid, R);
}
public static void merge(int[] arr, int L, int M, int R) {
int[] help = new int[R - L + 1];
int i = 0;
int p1 = L;
int p2 = M + 1;
while (p1 <= M && p2 <= R) {
help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
}
// 要么p1越界,要么p2越界
// 不可能出现:共同越界
while (p1 <= M) {
help[i++] = arr[p1++];
}
while (p2 <= R) {
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[L + i] = help[i];
}
}
- 非递归版本
package class08;
public class Code02_MergeSort {
public static void merge(int[] arr, int L, int M, int R) {
int[] help = new int[R - L + 1];
int i = 0;
int p1 = L;
int p2 = M + 1;
while (p1 <= M && p2 <= R) {
help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
}
// 要么p1越界,要么p2越界
// 不可能出现:共同越界
while (p1 <= M) {
help[i++] = arr[p1++];
}
while (p2 <= R) {
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[L + i] = help[i];
}
}
public static void mergeSort2(int[] arr) {
// 这里就不用排序
if (arr == null || arr.length < 2) {
return;
}
int step = 1;
int N = arr.length;
// 等于N的话不需要,你想想,你和一个空的数组去比,有意思吗?
while (step < N) {
// L是第一个左组的下标
int L = 0;
while (L < N) {
int M = 0;
// 这样M就不会越界,怎么会有越界的情况呢?比如元素个数有2^31-1个,现在step=2^30了,那么接下来如果直接 L + step - 1 可能就会越界。
if (N - L >= step) {
M = L + step - 1;
} else {
M = N - 1;
}
// 说明没有右组
if (M == N - 1) {
break;
}
// 右组第一个数
int R = 0;
if (N - 1 - M >= step) {
R = M + step;
} else {
R = N - 1;
}
merge(arr, L, M, R);
if (R == N - 1) {
break;
} else {
L = R + 1;
}
}
// 这里主要是怕溢出,如果数组长度N为15,步长1,2,4.....16,16超过了!看不懂的话就去看视频,具体定位到视频是00:35:50
if (step > N / 2) {
break;
}
step *= 2;
}
}
// for test
public static int[] generateRandomArray(int maxSize, int maxValue) {
int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
}
return arr;
}
// for test
public static int[] copyArray(int[] arr) {
if (arr == null) {
return null;
}
int[] res = new int[arr.length];
for (int i = 0; i < arr.length; i++) {
res[i] = arr[i];
}
return res;
}
// for test
public static boolean isEqual(int[] arr1, int[] arr2) {
if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
return false;
}
if (arr1 == null && arr2 == null) {
return true;
}
if (arr1.length != arr2.length) {
return false;
}
for (int i = 0; i < arr1.length; i++) {
if (arr1[i] != arr2[i]) {
return false;
}
}
return true;
}
// for test
public static void printArray(int[] arr) {
if (arr == null) {
return;
}
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
// for test
public static void main(String[] args) {
int testTime = 500000;
int maxSize = 100;
int maxValue = 100;
System.out.println("测试开始");
for (int i = 0; i < testTime; i++) {
int[] arr1 = generateRandomArray(maxSize, maxValue);
int[] arr2 = copyArray(arr1);
mergeSort1(arr1);
mergeSort2(arr2);
if (!isEqual(arr1, arr2)) {
System.out.println("出错了!");
printArray(arr1);
printArray(arr2);
break;
}
}
System.out.println("测试结束");
}
}
快速排序
递归方法
package class08;
import java.util.Stack;
public class Code03_PartitionAndQuickSort {
// 以数字x为参考值,小于等于x的放在左边,大于x的放在右边。
public static void splitNum1(int[] arr) {
int lessEqualR = -1;
int index = 0;
int N = arr.length;
// 遍历所有的数字
while (index < N) {
// 如果小于等于最后一个数,将这个值与小于等于最后一个数的区的下一个值互换。
if (arr[index] <= arr[N - 1]) {
swap(arr, ++lessEqualR, index++);
} else {
// 如果大于最后一个数,跳过当前值,直接下一个值
index++;
}
}
}
// 小于x的放在左边,大于x的放在右边,等于x的放在中间
public static void splitNum2(int[] arr) {
int N = arr.length;
int lessR = -1;
int moreL = N - 1;
int index = 0;
while (index < moreL) {
if (arr[index] < arr[N - 1]) {
// 如果当前数值小于最后一个值,那么将这个数值与小于最后一个值的区间的下一个元素进行交换,然后小于区间向后扩大一位元素
swap(arr, ++lessR, index++);
} else if (arr[index] > arr[N - 1]) {
// 如果当前数值大于最后一个值,那么将这个数值与大于最后一个值的区间的前一个元素进行交换,然后大于区间向前扩大一位元素
// WARNNING:index不变,因为这个数字还没有看呢!
swap(arr, --moreL, index);
} else {
// 如果相同,index不变
index++;
}
}
// 最后一个数字归位
swap(arr, moreL, N - 1);
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
// arr[L...R]范围上,拿arr[R]做划分值,
// L....R < = >
public static int[] partition(int[] arr, int L, int R) {
int lessR = L - 1;
int moreL = R;
int index = L;
while (index < moreL) {
if (arr[index] < arr[R]) {
swap(arr, ++lessR, index++);
} else if (arr[index] > arr[R]) {
swap(arr, --moreL, index);
} else {
index++;
}
}
// 最后一个数字归位
swap(arr, moreL, R);
return new int[] { lessR + 1, moreL };
}
public static void quickSort1(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
process(arr, 0, arr.length - 1);
}
public static void process(int[] arr, int L, int R) {
// 越界或者只有一个数字
if (L >= R) {
return;
}
int[] equalE = partition(arr, L, R);
process(arr, L, equalE[0] - 1);
process(arr, equalE[1] + 1, R);
}
}
非递归方法
package class08;
import java.util.Stack;
public class Code03_PartitionAndQuickSort {
// 非递归方法
public static class Job {
public int L;
public int R;
public Job(int left, int right) {
L = left;
R = right;
}
}
public static void quickSort2(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
Stack<Job> stack = new Stack<>();
stack.push(new Job(0, arr.length - 1));
while (!stack.isEmpty()) {
Job cur = stack.pop();
int[] equals = partition(arr, cur.L, cur.R);
// 但是你想一想,有没有这种可能,就是根本没有x的区域。
// 例如: 2 2 3 5 6 1,可以看到,没有小于1的区域,也就没有子任务
if (equals[0] > cur.L) { // 有 < 区域
stack.push(new Job(cur.L, equals[0] - 1));
}
if (equals[1] < cur.R) { // 有 > 区域
stack.push(new Job(equals[1] + 1, cur.R));
}
}
}
}