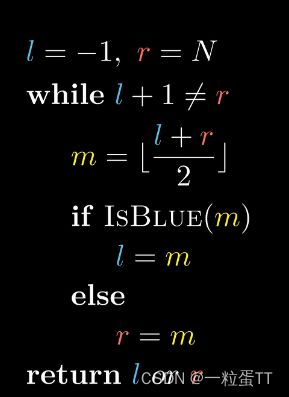【LeetCode704.二分查找】——二分查找方法汇总
索引:
-
- 例题:704.二分查找:
-
- 初步思考:
- 进一步思考:
- 总结:
- 拓展延伸:
-
- First Occurance:
- Last Occurance:
- Closest:
- 更优化算法:
- 补充:
例题:704.二分查找:
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
链接:https://leetcode.cn/problems/binary-search/
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
- 你可以假设 nums 中的所有元素是不重复的。
- n 将在 [1, 10000]之间。
- nums 的每个元素都将在 [-9999, 9999]之间。
初步思考:
关键词:有序、不重复。进而选择使用二分查找的方法,对数组进行遍历。
- 过程:
设定左右指针
找出中间位置,并判断该位置值是否等于 target
nums[mid] == target 则返回该位置下标
nums[mid] > target 则右侧指针移到中间
nums[mid] < target 则左侧指针移到中间
时间复杂度:O(logN)
第一种方法,也就是定义 target 是在一个在左闭右闭的区间里[left, right] (这个很重要非常重要)。
区间的定义这就决定了二分法的代码应该如何写,因为定义target在[left, right]区间,所以有如下两点:
- while (left <= right) 要使用 <= ,因为left == right是有意义的,所以使用 <=
- if (nums[middle] > target) right 要赋值为 middle - 1,因为当前这个nums[middle]一定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1
代码如下:
#include进一步思考:
如果说定义 target 是在一个在左闭右开的区间里,也就是**[left, right)** ,那么二分法的边界处理方式则截然不同。
有如下两点:
- while (left < right),这里使用 < ,因为left == right在区间[left, right)是没有意义的
- if (nums[middle] > target) right 更新为 middle,因为当前nums[middle]不等于target,去左区间继续寻找,而寻找区间是左闭右开区间,所以right更新为middle,即:下一个查询区间不会去比较nums[middle]
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size(); // 定义target在左闭右开的区间里,即:[left, right)
while (left < right) { // 因为left == right的时候,在[left, right)是无效的空间,所以使用 <
int middle = left + ((right - left) >> 1);
if (nums[middle] > target) {
right = middle; // target 在左区间,在[left, middle)中
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间,在[middle + 1, right)中
} else { // nums[middle] == target
return middle; // 数组中找到目标值,直接返回下标
}
}
// 未找到目标值
return -1;
}
};
总结:
二分法对于开闭区间的理解十分重要,对于区间的边界处理不当会导致结果的错误。
参考:手把手带你撕出正确的二分法 | 二分查找法 | 二分搜索法_哔哩哔哩_bilibili
拓展延伸:
Binary Search两大基本原则:
- 每次都要缩减搜索区域。
- 每次缩减不能排除潜在答案。
(这部分代码仍存在死循环的bug)
First Occurance:
寻找元素第一次出现时的位置:
循环条件:l 寻找元素最后一次出现时的位置: 循环条件:l 寻找与元素大小最接近的数的位置: 循环条件:l 参考链接:https://www.bilibili.com/video/BV1Ng4y1q7E3?spm_id_from=333.999.0.0 在b站中看到一个视频,对二分查找再一次进行了较为详细的讲解,其思路与以上的又大为不同,可以说是这类题目的一个通法,看完后,给我了大大的启发,有了融会贯通的感觉。该视频给出了关于二分查找这类问题的一个通用模板。 视频链接:二分查找为什么总是写错?_哔哩哔哩_bilibili 这里将l的值设置为-1,r的值设置为N,这与之前的方法都是大为不同的。这种类型其实就是左开右开的类型,可以让中间值m一直处于[0,N]以内。同时,在更新指针时,避免了多次讨论l=m+1,r=m-1等情况,统一为l=m,r=m,可以作为一种通用的方法。这样我们的问题就转换为了以下步骤: 视频中还给出了四个具体的例子: 本文参考了网上多位大佬的视频教程以及文字教程,属于是对这类二分查找问题的一次较为深入的学习,在学习过程中记录下来了以上笔记,总结了各种不同的算法思路以及方法。 数组在作为参数传入函数时,数组的大小并不会传入,数组是由指针的形式传入函数的。所以在函数中需要访问原数组大小时候,需要将原数组的长度一并传入。 (6条消息) C语言的那些坑(数组做参数计算大小问题)_零一匠的博客-CSDN博客 //寻找某数第一次出现
int FirstOccurance(int nums[], int target, int length)
{
int l = 0, r = length - 1;
while (l < r)
{
int mid = l + (r - l) / 2;
if (nums[mid] < target)
{
l = mid+1;
}
else {
r = mid;
}
}
return l;
}
Last Occurance:
//寻找某数最后一次出现
int LastOccurance(int nums[], int target, int length)
{
int l = 0, r = length - 1;
while (l < r)
{
int mid = l + (r - l+1) / 2;//向上取整防止死循环
if (nums[mid] > target)
{
r = mid - 1;
}
else {
l = mid;
}
}
return l;
}
Closest:
//寻找最接近的值
int Closest(int nums[], int target, int length)
{
int l = 0, r = length - 1;
while (l < r-1)
{
int mid = l + (r - l) / 2;
if (nums[mid] < target)
{
l = mid;
}
else {
r = mid;
}
}
if (nums[r] < target)
{
return r;
}
else if(nums[r]>target)
{
return 1;
}
else
{
return target - nums[l] < nums[r] - target ? l : r;
}
}
更优化算法:

这边自己尝试将以上的伪代码进行了实现://找到第一个>=target的元素
int target1(int nums[], int target,int length)
{
int l = -1;
int r = length;
while ((l + 1) != r)
{
int m = (l + r) / 2;
//cout << "m=" << m<//找到最后一个//找到第一个>target的元素
int target3(int nums[], int target, int length)
{
int l = -1;
int r = length;
while ((l + 1) != r)
{
int m = (l + r) / 2;
//cout << "m=" << m<//找到最后一个<=target的元素
int target4(int nums[], int target, int length)
{
int l = -1;
int r = length;
while ((l + 1) != r)
{
int m = (l + r) / 2;
//cout << "m=" << m<补充: