深度学习之PyTorch实战计算机视觉--深度神经网络基础

3.1监督学习和无监督学习

3.1.1 监督学习

监督学习定义：提供一组输入数据和其对应的标签数据，然后搭建个模型，让模型在通过训练后准确地找到输入数据和标签数据之间的最优映射关系，在输入新的数据后，模型能够通过之前学到的最优映射关系快速地预测出这组新数据的标签，这就是个监督学习的过程。其中回归问题和分类问题使用监督学习的频次较高。
1.回归问题:使用监督学习方法，让我们搭建的模型通过训练后建立起一个连续的线性映射关系，即通过提供数据训练模型，让模型得到映射关系并能对新的输入数据进行预测，其中映射模型就是线性连续的对应关系。
2.分类问题：分类问题是搭建的模型再通过监督学习后建立起一个离散的映射关系。

3.1.2 无监督学习

1.无监督学习定义：提供一组没有任何标签的输入数据，将其在搭建好的模型中训练，对整个训练过程不做任何干涉，最后得到一个能够发现数据之间隐藏的映射模型，使用这个模型能够实现随新数据的分类，这就是一个无监督学习的过程。
2.聚类：无监督学习实现的分类只是将相似关系的数据聚集到一起，所以无监督学习现实的分类算法又叫做聚类
3.两种对比

	优点	缺点
监督学习	最后得到的模型更符合设计舍得需求和初衷	训练模型需要投入大量的时间和精力
无监督学习	更具有创造性，可以挖掘到数据之间意想不到的映射关系	结果可能也会向不好的方向发展

半监督学习和弱监督学习融合了监督学习和无监督学习各自有点，是一种更先进方法。

3.2欠拟合和过拟合

3.2.1欠拟合

欠拟合对己有数据的匹配性很差，不过对数据中的噪声不敏感
解决欠拟合问题方法：
（1）增加特征项：当没有准确把握数据特征时，会出现欠拟合。可以通过在模型中加入更多的和原有数据有重要相关的特性来训练搭建模型，以此获得更好的泛化能力。
（2）构造复杂的多项式：通过增加函数中的次项来增强模型的变化能力，从而提升其泛化能力。
（3）减少正则化参数：正则化参数实际上是为了防止过拟合，但是当模型出现欠拟合，就可以通过减少正则化参数来消除欠拟合。

3.2.2过拟合

过拟合特性的模型对数据的匹配性太好，所以对数据中的噪声非常敏感。
解决过拟合问题方法：
（1）增大训练的数据量：大多数过拟合是因为模型训练的数据量太小，导致搭建的模型过度捕捉了数据的有限特征，增加训练数据量后，模型自然就能不或数据的更多特性。
（2）采用正则化方法：正则一般指在目标函数之后加上范数，用来防止过拟合，实践中常用L0，L1，L2正则。
（3）Dropout方法：Dropout 方法在 网络模型中使用的频率较高 ，简单来说就是在神经网络模型进行前向传播的过程中，随机选取和丢弃指定层次之间的部分神经连接，因为整个过程是随机的，所以能有效防止过拟合发生。

3.3后向传播

深度学习中的后向传播主要用于对我们搭建的模型中的参数进行微调，在通过多次后向传播后，就可以得到模型的最优参数组合。
计算实例：

假设x0=1，x1=1,b=-1,w0=0.5,w1=0.5,
如图激活函数为

计算方法：

3.4损失和优化

3.4.1损失函数

1.均方误差函数（Mean Square Error ，简称 MSE）:是计算预测值与真实值之差的平方的期望值，可用于评价数据的变化程度，其得到的值越小，则说明模型预测值具有越好的精确度，均方误差函数的计算如下：

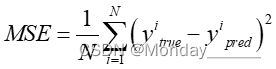
2.均值根误差函数（Root Mean Square Error ，简称 RMSE）：在均方误差函数 的基础上进行了 改良 ，计 方误差 算术平方根值，其得到的值越 小，则说明 模型的预测值具有越 好的精确度 均方根误差函数的计 如下：

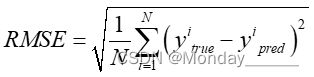
3.平均绝对误差函数（Mean Absolute Error, MAE ） 算的是绝对误差的平均值，绝对误差即模型预值和真实值之间的绝对值，能更好地反映预测值误差际情况，其得到的值越小，则说明模型的预测值具有越好的精确度。平均绝对误差函数如下：

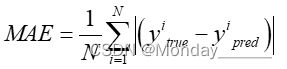
3.4.2优化函数

1.梯度下降 （Gradient Descent 简称 GD ） 是参数优化的方法
梯度：梯度其实是将多元函数的各个参数球的的偏导数以向量的形式展现出来，也叫做多元函数的梯度。二元函数 f(x,y)分别对元函数中的x,y求偏导数，然后把参数x,y求得的偏导数写成向量的形式， 即(∂f/∂x,∂f/∂y)，这就是二元函数 f(x,y )的梯度。
全局梯度下降公式：

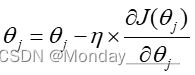
其中 ，训练样本总数为 n, j=0….n 可以将这里的等号看作编程中的赋值运算，θ是我们优化的参数对象， η是学习速率， J(θ)是损失函数， ∂J(θθ_j )/(∂θ_j )是根据损失函数来 θ的梯度。
学习速率：用于控制梯度更新的快慢，如果学习速率过快，参数的更新跨步就会变大，极易出现局部最优和抖动；如果学习速率过慢，梯度更新的迭代次数就会增加，参数更新，优化的时间也会变长，所以选择一个合理的学习速率是非常关键的。
2.批量梯度下降（（ Batch Gradient Descent ，简称 BGD）
原理概述：批量梯度下降就是将整个参与训练的数据集划分为若干个大小差不多的训练数据集 ，我们将其中一个训练数据集
个批量，每次用一个批量数据来对模型进行训练 ，井以这个批量计算得到的损失值为基准来对模型中的全部参数进行梯度更新，默认这个批 只使用一次，然后使用下一个批量数据来完成相同工作，直到所有批量的数据全部使用完毕。
实现方式：划分的批量个数为m，其中每一个批量包含batch个数据，那么一个批量的梯度下降的参数更新公式如下：

如果我们将批量划分得足够好 ，则计算损失函数的时间成本和模型训练的复杂度将会大大降低 ，不过仍然存在一些小问 题，就是选择批量梯度下降很容易导致优化函数的最终结果是局部最优解。
3.随机梯度下降（Stochastic Gradient Descent）简称 SGD
原理概述：随机梯度下降是通过随机的方式从整个参与练的数据集中选取部分来参与模型的训练，所以只要我们随机选取的据集大小合适就不用担心计算损失函数的时间成本和模型训练的复杂度 ，而且与整个参与训练的数据集大小没有关系。
实现方式：选取含 stochastic 个数据样本，那么随机梯度下降的参数更新公式如下：

4.Adam–自适应时刻估计方法（ Adaptive Moment Estim ation ，简称 Adam ）
Adam 在模型训练优化的过程中通过让每个参数获得自适应的学习率，来达到优化质量和速度的双重提升。

3.5激活函数

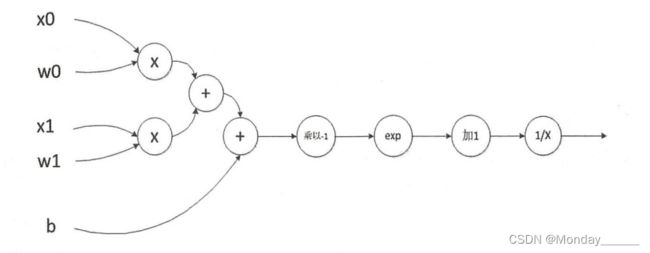
偏置：在神经网络中增加偏置的(bias)，可以让搭建的神经网络模型远离原点，没有偏置的函数必定会经过原点。
模型偏离原点的好处是能够使模型具有更强的变换能力，在面对不用的数据时拥有更好的泛化能力。

3.6GPU和CPU

在深度学习模型中生成的参数结构都是张量(tensor)形式的，之前我们已经了解了矩阵和张量是如何进行算术运算的，其中实矩阵和张量是一种并行运算，所以张量的算术运算在GPU的加持下会获得比CPU更快速，高校的计算能力，因此在对学习深度学习参数的训练和优化过程中，GPU能够为我们提供更多的帮助。