树之二叉排序树（二叉搜索树）

什么是排序树

说一下普通二叉树可不是左小右大的 

插入的新节点是以叶子形式进行插入的

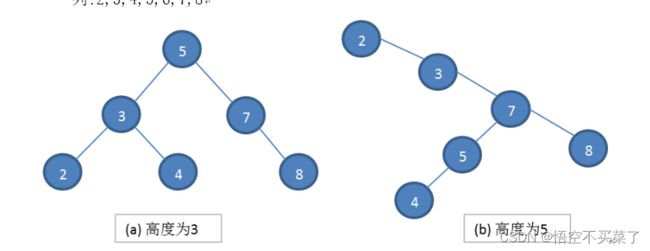
二叉排序树的中序遍历结果是一个升序的序列

下面是两个典型的二叉排序树 

 

 

 二叉排序树的操作

 构造树的过程即是对无序序列进行排序的过程。

 存储结构

 通常采用二叉链表作为存储结构 不能

 插入算法

 

 下面插入一个图解

上面的×就表示会在当前位置给delete掉一个结点 

 查找算法

 

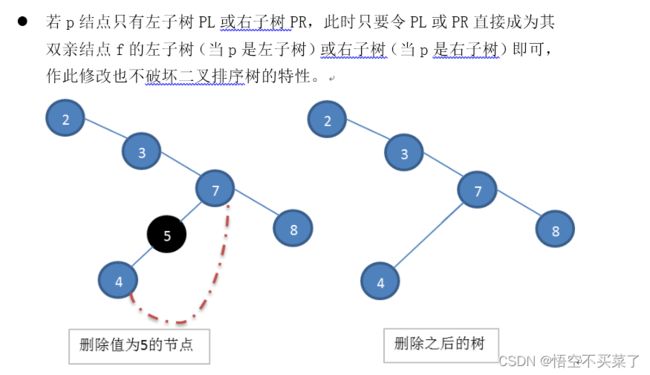
 删除算法

  

 

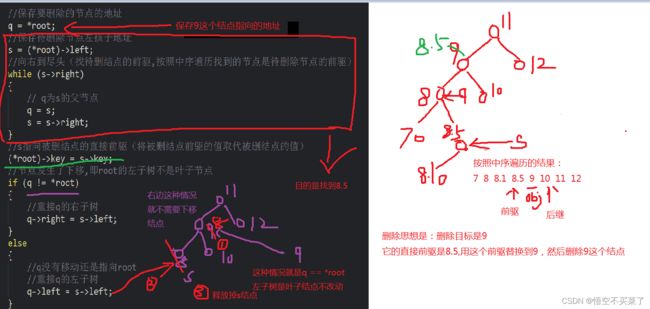
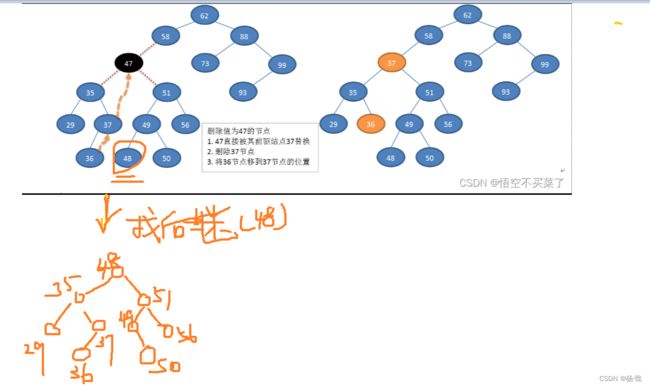
第三种情况：你删除的结点下面就是说还有左右子树，那么这个时候，我们就要去找到这棵树中序遍历结果之后的直接前驱或者直接后继，然后把这个前驱或者后继给按到删除结点这个位置上，将它下面的树移到被替换结点的位置

删除操作的具体讲解

重点讲解一下删除节点的核心分析

这里在补一张中序遍历的递归调用图

 

  直接上代码

在上代码之前，先来说一下，二叉搜索树很多方法都利用了递归的思想，许多说明我都放到代码注释里面了，可以结合下面的这张图进行思维分析

 

先来看c语言代码（algorithm/bst/bst1.c）

#include 
#include 

typedef int key_type;
typedef struct _node
{
    key_type key;
    struct _node *left;
    struct _node *right;
}node, *pnode;

void insert_bst(pnode *root, key_type key)
{
    //初始化插入结点
    pnode p = (pnode)malloc(sizeof(node));
    if (p != NULL)
    {
        p->key = key;//把值给放进去
        p->left = p->right = NULL;
    }

    //空树的时候，直接作为根结点
    if (*root == NULL)
    {
        *root = p;
        return;
    }
    //插入到当前结点的左孩子
    if ((*root)->left == NULL && (*root)->key > key)
    {
        (*root)->left = p;//直接在堆上面指就可以了
        return;
    }

    //插入到当前结点的右孩子
    if ((*root)->right == NULL && (*root)->key < key)
    {
        (*root)->right = p;
        return;
    }

    //上面都没有进入，说明结点就要往下继续存放
    //需要先把我们分配的结点内存给释放掉
    free(p);
    //左子树递归
    if ((*root)->key > key) 
    {
        insert_bst(&(*root)->left, key);
    }
    //右子树递归
    else if((*root)->key < key) 
    {
        insert_bst(&(*root)->right, key);
    }
}

//根据关键字删除某个结点，成功返回1,失败返回0
int delete_bst(pnode *root, key_type key)
{
    if (*root == NULL)
    {
        return 0;//这是一棵空树
    }
    if ((*root)->key == key)
    {
        pnode pbak1, pmove;
        //判断右子树是否为空，为空，只需要重接左子树
        if ((*root)->right == NULL)
        {
            //把当前结点的左子树接上去就可以了
            pbak1 = *root;//当前结点备份等会释放
            //改变在栈上面一级指针的指向
            *root = (*root)->left;
            //删除
            free(pbak1); 
        }
        //左子树为空的情况下，只需要重接右子树就行了
        else if ((*root)->left == NULL)
        {
            //删除结点的空间备份
            pbak1 = *root;
            *root = (*root)->right;//改变栈上结点的指向
            free(pbak1);
        }
        //左右子树都不为空
        else
        {
            //我们要找到直接前驱或者一个直接后继
            //前驱就是当前结点下一个结点左边结点的右边(尽头)，所以先把root指向了左结点
            pbak1 = *root;//删除结点的一个备份
            pmove = (*root)->left;//左边等会要接接上
            //再来循环右边
            //注意的问题是我们需要指向一个直接前驱的父结点
            //以便于用来更改当前的子树结点，也就是被删除结点的下一个结点要连接上去
            while (pmove->right)
            {
                pbak1 = pmove;//前驱结点的父节点
                pmove = pmove->right;//这个是指向了我们需要的前驱结点
            }

            //s指向了前驱结点，将s放到root结点上面
            (*root)->key = pmove->key;//改变了值，不是地址,等会吧pmove给释放掉

            //重接一下下面结点的子树
            //如果pbak1没有移动过，那么pbak1->left = pmove ->left;
            if (pbak1 == *root)
            {
                pbak1->left = pmove->left;
            }
            else 
            {
                //如果移动过，那么pbak1->right就要改变
                pbak1->right = pmove->left;
            }
            //释放掉pmove这个结点
            free(pmove);
        }
        return 1;
    }
    //没有找到的情况下，我们需要遍历树
    else if (key < (*root)->key) 
    {
        //直接走左子树
        //这里必须return ,不然找到了也会false
        return delete_bst(&(*root)->left, key);
    }
    else if (key > (*root)->key)
    {
        //大于当前结点就直接走右子树
        return delete_bst(&(*root)->right, key);
    }
    return 0;
}

//查找元素，找到返回结点指针，没找到返回NULL
//找结点，传入一个一级指针就好了
pnode search_bst(pnode root, key_type key)
{
    if (root == NULL)
    {
        return NULL;
    }
    //查找右子树
    if (key > root->key)
    {
        return search_bst(root->right, key);
    }
    //查找左子树
    else if (key < root->key)
    {
        return search_bst(root->left, key);
    }
    else 
    {
        return root;
    }
}

//查找最小的关键字，空树时返回NULL
pnode search_min_bst(pnode root)
{
    if (root == NULL)
    {
        return NULL;
    }
    //最小的话应该就是最左边孩子
    if (root->left == NULL)
    {
        return root;//叶子结点下面都是NULL
    }
    else 
    {
        return search_min_bst(root->left);
    }
}

//查找最大关键字，空树时返回NULL
pnode search_max_bst(pnode root)
{
    if (root == NULL)
    {
        return NULL;
    }
    //找到最后的孩子
    if (root->right == NULL)
    {
        return root;
    }
    else
    {
        //一直往右边找，直到没有有孩子结点
        return search_max_bst(root->right);
    }
}

//中序遍历二叉树
void inorder_traverse_bst(pnode root)
{
    if (root != NULL)
    {
        //遍历左子树
        //先走到最左边，依次调用结束，返回打印
        inorder_traverse_bst(root->left);
        //走到最后一个结束，打印，中间根结点也会打印
        printf("%d ", root->key);
        //然后走右边开始打印
        inorder_traverse_bst(root->right);
    }
}



int main()
{
    //创建一棵二叉树
    pnode root = NULL;
    insert_bst(&root, 3);
    insert_bst(&root, 8);
    insert_bst(&root, 2);
    insert_bst(&root, 5);
    insert_bst(&root, 4);
    insert_bst(&root, 9);
    insert_bst(&root, 11);

    //中序遍历二叉树
    inorder_traverse_bst(root);

    delete_bst(&root, 2);
    printf("\n---------------------\n");

    inorder_traverse_bst(root);

    return 0;
}

再来看java的运行代码（algorithm/bst1）

package com.pxx.tree.bst1;
class Node {
    int key;
    Node left, right;

    //这里就是在new的时候可以出初始化一个头结点
    public Node(int key) {
        this.key = key;
        this.left = this.right = null;
    }
}

class BstTree {
    //插入结点
    public Node insertBst(Node root, int key) {
        if (root == null) {
            //直接返回这个新结点
            //指到最后可添加位置，也是直接指向这个新节点
            return new Node(key);
        }
        if (key < root.key) {
            //往左边走
            root.left = insertBst(root.left, key);
        } else if(key > root.key) {
            //往右边走
            root.right = insertBst(root.right, key);
        }
        return root;//这里返回root的意思也就是中间的结点必须连上
    }

    //删除结点
    public Node deleteBST(Node root, int key) {
        if (root == null) {
            return root;
        }

        if (key < root.key) {
            root.left = deleteBST(root.left, key);
        } else if (key > root.key) {
            root.right = deleteBST(root.right, key);
        } else {
            //找到了这个结点
            if (root.left == null) {
                //直接返回这个结点的右结点给上一个节点
                return root.right;
            } else if (root.right == null) {
                return root.left;
            }

            //上面都没有进入，说明有左右子树，需要结点上一移动
            //先改变查找到结点的值，我们需要用它的直接后继来替换
            //也就是找到它右边的结点，然后不停的左边，一直到尽头
            root.key = minValue(root.right);
            //改变结点之间的连接
            root.right = deleteBST(root.right, root.key);
        }
        return root;
    }

    // 寻找最小值
    //从某个结点一直找到最左边就是最小值
    public int minValue(Node root) {
        while (root != null && root.left != null) {
            root = root.left;
        }
        return root.key;
    }

    //中序遍历这个结点
    public void inorderTraverseBst(Node root) {
        if (root != null) {
            //先打印左边
            inorderTraverseBst(root.left);
            System.out.print(root.key + " ");
            inorderTraverseBst(root.right);
        }
    }

    //查找某一个元素
    public Node searchBST(Node root, int key) {
        if (root == null || root.key == key) {
            return root;
        }

        if (key < root.key) {
            return searchBST(root.left, key);
        }

        return searchBST(root.right, key);
    }



}

public class Solution {
    public static void main(String[] args) {
        BstTree bstTree = new BstTree();
        Node root = null;
        //root在堆上就已经建立空间
        root = bstTree.insertBst(root, 3);
        bstTree.insertBst(root, 8);
        bstTree.insertBst(root,2);
        bstTree.insertBst(root,5);
        bstTree.insertBst(root,4);
        bstTree.insertBst(root,9);
        bstTree.insertBst(root,1);

        //中序遍历这片空间
        bstTree.inorderTraverseBst(root);

        System.out.println("-----------------");
       bstTree.deleteBST(root,2);
       bstTree.deleteBST(root,8);

        bstTree.inorderTraverseBst(root);
    }

}

好了，说到这。