二叉排序树/二叉查找树及其基本操作
一、二叉排序树
二叉排序树,又称二叉查找树(BST(Binary Sort/Search Tree) )或者是一棵空树,或者是具有下列特性的二叉树:
(1)若左子树非空,则左子树上所有结点的值均小于根结点的值。
(2)若右子树非空,则右子树删所有结点的值均大于根结点的值。
(3)左右子树分别为一棵二叉排序树。
根据二叉排序树的定义,左子树结点值<根结点值<右子树结点值,则对二叉排序树进行中序遍历,可以得到一个递增的有序序列。如果有相同的值,可以将该节点放在左子节点或右子节点。
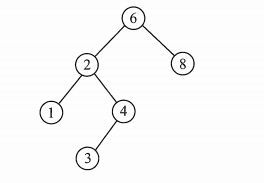
E.g:下图所示的二叉排序树的中序遍历序列为1 2 3 4 5 6 8。
二、二叉排序树的基本操作
1、添加子结点
1.1、实现思路
(1)若添加结点为空,则无法添加;
(2)若添加结点的值小于当前结点的值,根据二叉排序树的定义,我们需要向当前结点的左子树添加结点。若当前结点的左子树为空,则直接添加成为当前结点的左子树;若当前结点的左子树不为空,则递归向当前结点的左子树遍历。
(3)若添加结点的值大于等于当前结点的值,根据二叉排序树的定义,我们需要向当前结点的右子树添加结点。若当前结点的右子树为空,则直接添加成为当前结点的右子树;若当前结点的右子树不为空,则递归向当前结点的右子树遍历。
1.2、实现代码
public void add(Node node) {
if(node==null) {//添加结点为空
return;
}
if(node.value<this.value) {//添加结点值小于当前结点值,根据二叉排序树定义应向左边寻找
if(this.left==null) {//当前结点没有左孩子直接放在当前结点左边
this.left=node;
}else {
this.left.add(node);//否则递归向当前结点的左子树遍历
}
}else {//添加结点值大于等于当前结点值,根据二叉排序树定义应向右边寻找
if(this.right==null) {//当前结点没有右孩子直接放在当前结点右边
this.right=node;
}else {
this.right.add(node);//否则递归向当前结点的右子树遍历
}
}
}
2、查找子结点
2.1 实现思路
(1)若查找值等于当前结点值则直接返回;
(2)若查找值小于当前结点的值,根据二叉排序树的定义,我们需要向当前结点的左子树查找。若当前结点的左子树为空,则无法找到返回为空;若当前结点的左子树不为空,则递归向当前结点的左子树查找。
(3)若查找值大于等于当前结点的值,根据二叉排序树的定义,我们需要向当前结点的右子树查找。若当前结点的右子树为空,则无法找到返回为空;若当前结点的右子树不为空,则递归向当前结点的右子树查找。
2.2 实现代码
public Node search(int value) {
if(value==this.value) {//查找值等于当前结点值直接返回
return this;
}else if(value<this.value) {//查找值小于当前结点值,根据二叉排序树定义则向左子树查找
if(this.left==null) {//当前结点的左子树为空则找不到
return null;
}
return this.left.search(value);
}else {//查找值大于等于当前结点值,根据二叉排序树定义则向右子树查找
if(this.right==null) {//当前结点的右子树为空则找不到
return null;
}
return this.right.search(value);
}
}
3、删除子结点
3.1 实现思路
3.1.1 删除叶子结点
(1)是否为叶子结点的判断条件为:targetNode.left == null && targetNode.right==null,即左右结点均为空;
(2)若targetNode为左子结点则将parent的左子结点置空即删除,即parent.left=null;若targetNode为右子结点则将parent的右子结点置空即删除,即parent.right=null。
3.1.2 删除只有一棵子树的结点
(1)是否为只有一棵子树的结点:targetNode.left ==null || targetNode.right ==null,即targetNode.left 和 targetNode.right 中有且仅有一个为 null;
(2)若删除的结点有左子结点时,当targetNode是 parent 的左子结点,使parent.left=targetNode.left;当targetNode是 parent 的右子结点,使parent.right=targetNode.left;最后使root=targetNode.left。
(3)若删除的结点有右子结点时,当targetNode是 parent 的左子结点,使parent.left=targetNode.right;当targetNode是 parent的右子结点,使parent.right=targetNode.right;最后使root=targetNode.right。
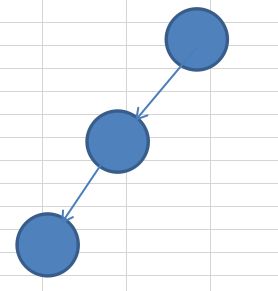
若删除的结点有左子结点时,两种示意图:
(1)当targetNode是 parent 的左子结点
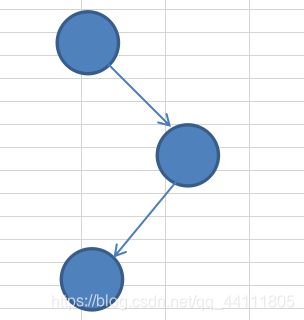
(2)当targetNode是 parent的右子结点
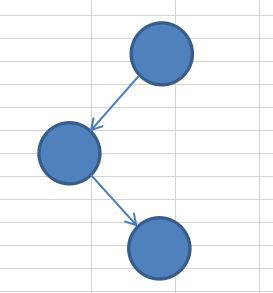
若删除的结点有右子结点时,两种示意图:
(1)当targetNode是 parent 的左子结点
(2)当targetNode是 parent的右子结点
3.1.3 删除有两棵子树的结点
(1)先找到删除结点 targetNode,再找到其父结点parent;
(2)利用递归在 targetNode的左子树中寻找值最小的结点,用临时变量temp保存;
(3)删除该最小结点:delete(temp.value),再将 targetNode.value 设置为 temp即可。
3.2 实现代码
//结点类Node
//查找删除结点的父结点
public Node searchParent(int value) {
if((this.left!=null&&this.left.value==value)||(this.right!=null&&this.right.value==value)) {
return this;//若当前结点即为需要删除结点的父结点直接返回
}else {
if(value<this.value&&this.left!=null) {//删除结点值小于当前结点值且当前结点的左子树不为空,则向左子树递归查找删除
return this.left.searchParent(value);
}else if(value>=this.value&&this.right!=null) {//删除结点值大于等于当前结点值且当前结点的右子树不为空,则向右子树递归查找删除
return this.right.searchParent(value);
}else {//左右子树均未找到即返回空
return null;
}
}
}
//二叉排序树定义类SortTree
//删除子结点
public void delete(int value) {
if(root==null) {//根结点为空无法操作直接返回
return;
}else {
Node targetNode=search(value);//找到要删除的结点targetNode
if(targetNode==null) {//若没有找到要删除的结点直接返回
return;
}
if(root.left==null&&root.right==null) {//若二叉排序树只有一个结点即根结点,将根结点置空即删除
root=null;
return;
}
Node parent=searchParent(value);//寻找targetNode的父结点
if(targetNode.left==null&&targetNode.right==null) {//删除结点为叶子结点
//判断targetNode是父结点的左子结点还是右子结点
if(parent.left!=null&&parent.left.value==value) {//targetNode为左子结点则将parent的左子结点置空即删除
parent.left=null;
}else if(parent.right!=null&&parent.right.value==value) {//targetNode为右子结点则将parent的右子结点置空即删除
parent.right=null;
}
}else if(targetNode.left!=null&&targetNode.right!=null){//删除有两颗子树的节点
int min=delRightMinTree(targetNode.right);
targetNode.value=min;
}else {//删除只有一颗子树的结点
if(targetNode.left!=null) {//若删除的结点有左子结点
if(parent!=null) {
if(parent.left.value==value) {//若targetNode是 parent 的左子结点
parent.left=targetNode.left;
}else { //若targetNode是 parent 的右子结点
parent.right=targetNode.left;
}
}else {
root=targetNode.left;
}
}else {//若删除的结点有右子结点
if(parent!=null) {
if(parent.left.value==value) {//若targetNode是 parent 的左子结点
parent.left=targetNode.right;
}else {//若targetNode是 parent的右子结点
parent.right=targetNode.right;
}
}else {
root=targetNode.right;
}
}
}
}
}
/**
* @param node 二叉排序树的根结点
* @return 返回的 以node为根结点的二叉排序树的最小结点的值
*/
public int delRightMinTree(Node node) {
Node temp=node;
while(temp.left!=null) {//循环的查找左子节点,会找到最小值(因为左子树结点值<根结点值<右子树结点值)
temp=temp.left;
}
delete(temp.value);//退出循环时temp指向最小结点,则删除最小值结点,此时该结点必为左叶子结点
return temp.value;
}
三、完整实现代码
package Tree;
public class BinarySortTree {
public static void main(String[] args) {
int[] arr= { 7, 3, 10, 12, 5, 1, 9};
SortTree binarysorttree = new SortTree();
for(int i=0;i<arr.length;i++) {
binarysorttree.add(new Node(arr[i]));
}
System.out.println("初始二叉排序树的中序遍历");
binarysorttree.inOrder();// 1,3, 5, 7, 9, 10, 12
//测试删除叶子结点
binarysorttree.delete(1);
System.out.println("删除叶子结点后二叉排序树的中序遍历");
binarysorttree.inOrder();//3, 5, 7, 9, 10, 12
//测试删除只有一颗子树的结点
binarysorttree.delete(3);
System.out.println("删除只有一颗子树的结点后二叉排序树的中序遍历");
binarysorttree.inOrder();//5, 7, 9, 10, 12
//测试删除有两颗子树的节点
binarysorttree.delete(10);
System.out.println("删除有两颗子树的节点后二叉排序树的中序遍历");
binarysorttree.inOrder();//5, 7, 9, 12
}
}
class SortTree{
private Node root;//二叉排序树根结点
public Node getRoot() {//获取二次排序树根结点
return root;
}
public void add(Node node) {//添加子结点
if(root==null) {//若根结点为空直接让添加结点成为子结点
root=node;
}else {
root.add(node);
}
}
public void inOrder() {//中序遍历
if(root!=null) {//若根结点不为空则调用结点的inOrder
root.inOrder();
}else {
System.out.println("二叉排序树为空,无法遍历!");
}
}
public Node search(int value) {//查找子结点
if(root==null) {
return null;
}else{
return root.search(value);
}
}
public Node searchParent(int value) {//查找父结点
if(root==null) {//根结点为空无法操作返回为空
return null;
}else {
return root.searchParent(value);
}
}
//删除子结点
public void delete(int value) {
if(root==null) {//根结点为空无法操作直接返回
return;
}else {
Node targetNode=search(value);//找到要删除的结点targetNode
if(targetNode==null) {//若没有找到要删除的结点直接返回
return;
}
if(root.left==null&&root.right==null) {//若二叉排序树只有一个结点即根结点,将根结点置空即删除
root=null;
return;
}
Node parent=searchParent(value);//寻找targetNode的父结点
if(targetNode.left==null&&targetNode.right==null) {//删除结点为叶子结点
//判断targetNode是父结点的左子结点还是右子结点
if(parent.left!=null&&parent.left.value==value) {//targetNode为左子结点则将parent的左子结点置空即删除
parent.left=null;
}else if(parent.right!=null&&parent.right.value==value) {//targetNode为右子结点则将parent的右子结点置空即删除
parent.right=null;
}
}else if(targetNode.left!=null&&targetNode.right!=null){//删除有两颗子树的节点
int min=delRightMinTree(targetNode.right);
targetNode.value=min;
}else {//删除只有一颗子树的结点
if(targetNode.left!=null) {//若删除的结点有左子结点
if(parent!=null) {
if(parent.left.value==value) {//若targetNode是 parent 的左子结点
parent.left=targetNode.left;
}else { //若targetNode是 parent 的右子结点
parent.right=targetNode.left;
}
}else {
root=targetNode.left;
}
}else {//若删除的结点有右子结点
if(parent!=null) {
if(parent.left.value==value) {//若targetNode是 parent 的左子结点
parent.left=targetNode.right;
}else {//若targetNode是 parent的右子结点
parent.right=targetNode.right;
}
}else {
root=targetNode.right;
}
}
}
}
}
/**
* @param node 二叉排序树的根结点
* @return 返回的 以node为根结点的二叉排序树的最小结点的值
*/
public int delRightMinTree(Node node) {
Node temp=node;
while(temp.left!=null) {//循环的查找左子节点,会找到最小值(因为左子树结点值<根结点值<右子树结点值)
temp=temp.left;
}
delete(temp.value);//退出循环时temp指向最小结点,则删除最小值结点,此时该结点必为左叶子结点
return temp.value;
}
}
class Node{
int value;
Node left;
Node right;
public Node(int value) {//Node的构造函数(无返回值)
this.value=value;
}
@Override
public String toString() {//重写toString方法
return "Node [value=" + value + "]";
}
public void inOrder() {//中序遍历二叉排序树得到有序序列
if(this.left!=null) {
this.left.inOrder();
}
System.out.println(this);
if(this.right!=null) {
this.right.inOrder();
}
}
//添加子结点
public void add(Node node) {
if(node==null) {//添加结点为空
return;
}
if(node.value<this.value) {//添加结点值小于当前结点值,根据二叉排序树定义应向左边寻找
if(this.left==null) {//当前结点没有左孩子直接放在当前结点左边
this.left=node;
}else {
this.left.add(node);//否则递归向当前结点的左子树遍历
}
}else {//添加结点值大于等于当前结点值,根据二叉排序树定义应向右边寻找
if(this.right==null) {//当前结点没有右孩子直接放在当前结点右边
this.right=node;
}else {
this.right.add(node);//否则递归向当前结点的右子树遍历
}
}
}
//查找子结点
public Node search(int value) {
if(value==this.value) {//查找值等于当前结点值直接返回
return this;
}else if(value<this.value) {//查找值小于当前结点值,根据二叉排序树定义则向左子树查找
if(this.left==null) {//当前结点的左子树为空则找不到
return null;
}
return this.left.search(value);
}else {//查找值大于等于当前结点值,根据二叉排序树定义则向右子树查找
if(this.right==null) {//当前结点的右子树为空则找不到
return null;
}
return this.right.search(value);
}
}
//查找删除结点的父结点
public Node searchParent(int value) {
if((this.left!=null&&this.left.value==value)||(this.right!=null&&this.right.value==value)) {
return this;//若当前结点即为需要删除结点的父结点直接返回
}else {
if(value<this.value&&this.left!=null) {//删除结点值小于当前结点值且当前结点的左子树不为空,则向左子树递归查找删除
return this.left.searchParent(value);
}else if(value>=this.value&&this.right!=null) {//删除结点值大于等于当前结点值且当前结点的右子树不为空,则向右子树递归查找删除
return this.right.searchParent(value);
}else {//左右子树均未找到即返回空
return null;
}
}
}
}
运行结果:
初始二叉排序树的中序遍历
Node [value=1]
Node [value=3]
Node [value=5]
Node [value=7]
Node [value=9]
Node [value=10]
Node [value=12]
删除叶子结点后二叉排序树的中序遍历
Node [value=3]
Node [value=5]
Node [value=7]
Node [value=9]
Node [value=10]
Node [value=12]
删除只有一颗子树的结点后二叉排序树的中序遍历
Node [value=5]
Node [value=7]
Node [value=9]
Node [value=10]
Node [value=12]
删除有两颗子树的节点后二叉排序树的中序遍历
Node [value=5]
Node [value=7]
Node [value=9]
Node [value=12]
