关于ndarray对象知识总结

目录

0.引入

ndarray的轴

ndarray的属性

一、创建

（一）直接使用 np.array 创建

（二）使用NumPy中函数

二、索引

（一）一维数组

（二）多维数组

（三）布尔索引

        1.一维：

        2.二维：

（四）数组索引

        1.一维

        2.二维 

三、基本操作

（一）运算

广播原则

（二）方法

1.拆分与合并：

2.其他方法

①等差

②等比

③改数据类型

④统计量计算

⑤条件计算

⑥排序

⑦去重

（三）拷贝

        1.浅拷贝

        2.深拷贝

---

0.引入

        Ndarray 是 n 维数组对象，其维度可以是 n 维的，元素之间由空格分割，数组里的所有元素必须是相同的类型，若元素数据类型不同，则全部元素统一为存储空间最大的数据类型。

        对数组我们可以通过内置方法计算其各种统计量，如平均数、中位数等等

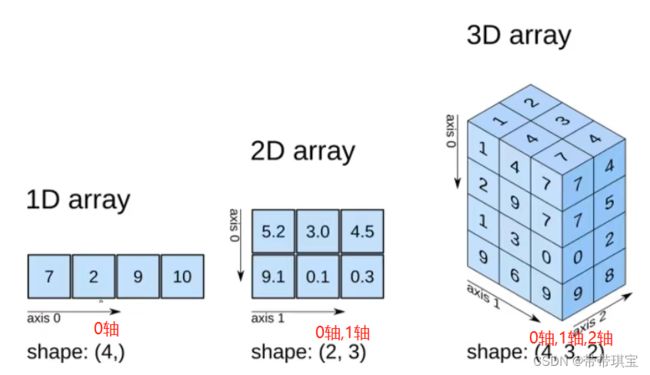
ndarray的轴

        数组有几个轴由维度决定：一维数组有一个轴，二维数组有两个轴，三维有三个（三维就是块、行、列）。

        对于轴号像我这样的小白可理解为轴的下标，如下对应关系

ndarray的属性

        查看方法：print(数组.属性)

# 区分
print(ndarry.dtype)    # 查看数组中的数据类型
print(type(ndarray))    # 查看数据类型是否是数组

• shape：数组的维度，如（4，1）是二维的，而（4，）是一维的，分别表示行数和列数
• dtype：数据类型，Ndarray支持的数据类型比Python本身更丰富，可自行指定，数组里的所有元素必须是相同的类型，若元素含有字符，则全部元素都是字符类型。
• ndim：数组的维度。
• size：数组中总元素数量，即 shape 中的行列乘积、itemsize：每个数组元素数量
• flat：将数组展开成一维，并返回迭代器，可用于遍历

a=np.array([[1,0,0],[0,1,0],[0,0,1]])

print(a)
print(type(a))
[[1 0 0]
 [0 1 0]
 [0 0 1]]


print(a.shape)
(3, 3)

print(a.ndim)
2

print(a.dtype)
int32

print(a.flat[0:])    # 这里是查看返回的一维数组
[1 0 0 0 1 0 0 0 1]

一、创建

（一）直接使用 np.array 创建

        numpy.array(object, dtype=None, copy=True, order=None, subok=False, ndmin=0)

        参数：

• object：必须，可以从常规的 python 列表、元组、数组或其他可迭代对象中创建数组，相当于把 object 复制过来成为数组（object 若是自己创建的序列要用 [ ] 框起来，否则会被当成另一个参数）
• dtype：可选，元素的类型由原序列中的元素类型确定，也可以自己通过dtype参数指定
• copy：可选，Python 中变量存储的是所指向的内存地址

        默认 True：复制数组时会重新开辟内存创建副本，在修改 a 数组的值时 b 数组不会变化，相当于：

a=np.array([1,2,3,4])
b=np.array(a)

        为 False：复制数组两数组会指向同一内存地址，两数组的值永远相同，相当于

a=np.array([1,2,3,4])
b=a

         更常用创建副本的方法：

a=np.array([1,2,3,4])
b=a.copy

• order：可选，涉及内存布局关系不大不作详解
• ndim：可选，指定数组维度
• subok：可选，默认 False：使用数组类型；为True：使用 object 内部原本的数据类型（列表会自动转换为数组）

l=[(1,2),(3,4),(5,6)]
a=np.array(range(1,10,2))
b=np.array(l)
print(a)
print(b)
print(b.ndim)


[1 3 5 7 9]

[[1 2]
 [3 4]
 [5 6]]

2

（二）使用NumPy中函数

        array.func< >，如：

函数	说明
arange(a,b,c)	b为必选，相当于range的数组版，返回ndarray类型，元素从a到b-1每隔c个数创建数组
ones(shape)	根据shape生成一个全1数组
zeros(shape)	根据shape生成全0数组
full(shape,value)	根据shape生成一个数组，每元素值全为value
eye(n)	一个正方形的n*n单位矩阵，对角线为1，其余为0
ones_like(a)	根据数组a的形状生成一个全1数组
zeros_like(a)	根据数组a的形状生成一个全0数组
full_like(a,value)	根据数组a的形状生成一个数组，每元素值全为value
linspace()	根据起止数据等间距地填充数据，形成数组
concatenate()	根据两个或多个数组合并成一个新数组

表格源自：https://www.cnblogs.com/guobin-/p/11211653.html 

        多维数组：如下是两块三行三列的数组

a=np.ones((2,3,3))
print(a)

[[[1. 1. 1.]
  [1. 1. 1.]
  [1. 1. 1.]]

 [[1. 1. 1.]
  [1. 1. 1.]
  [1. 1. 1.]]]

二、索引

        Ndarray采用索引机制，将每个元素映射到内存快上，按一定布局排列，可以通过索引访问、查找筛选、切片、修改元素等，暂时只研究一维二维的，每个例子都很重要呀

（一）一维数组

        形式类似列表与元组，值得注意的是，在进行切片之后对其操作实际还是操作的原数组，相当于原数组这一块的视图（不想更改使用 .copy() 进行复制），而列表切片之后是新的列表，开了新的内存地址

b=np.array([1,0,0,0,1,0,0,0,1])
print(b)
print(b[0:5:2][1])    # 不含stop
b[0:5:2][1]=1
print(b)


[1 0 0 0 1 0 0 0 1]
0
[1 0 1 0 1 0 0 0 1]

（二）多维数组

        多维数组每个 axis 都会有一个索引，行和列均从 0 开始，通过逗号分割进行查找，这是比较规范的用法，多尝试体验与 list 索引的差别

a=np.eye(5)
print(a)

# ①不含右端点，若为4会找不到[0,0,0,0,1]
print(a[0:5:2])

# ②逗号相当于分割取行和列，这个是规范用法，只有a[1]时取的是行
print(a[0:5:2,0:2])

# ③与list不同，链式表达是前面一步的结果传递到后面一步
   只有单个数值的时候与上面方法相同      
print(a[0:5:2][0:2])   

# 将axis理解为存放下标的框框，如果参数有axis等于n，就相当于对应的n-1个框中的下标进行变化，其它框中下标不变进行操作


[[1 0 0 0 0]
 [0 1 0 0 0]
 [0 0 1 0 0]
 [0 0 0 1 0]
 [0 0 0 0 1]]

[[1. 0. 0. 0. 0.]
 [0. 0. 1. 0. 0.]
 [0. 0. 0. 0. 1.]]

[[1. 0.]
 [0. 0.]
 [0. 0.]]

[[1. 0. 0. 0. 0.]
 [0. 0. 1. 0. 0.]]

（三）布尔索引

        使用布尔索引可以取到满足条件的数，如下代码通俗易懂解释何为布尔索引及使用方法：

        1.一维：

a=np.arange(1,10)
print(a)
print(a>5)
print(a[a>5])

[1 2 3 4 5 6 7 8 9]
[False False False False False  True  True  True  True]
[6 7 8 9]

         使用关系运算符：

a=np.arange(1,10)
print(a)
b=(a>7)|(a<4)
print(b)
print(a[b])


[1 2 3 4 5 6 7 8 9]
[ True  True  True False False False False  True  True]
[1 2 3 8 9]

        2.二维：

                (1)直接筛选返回一维数组

                        例1：

a=np.arange(1,21).reshape(5,4)
print(a)
print(a[a>5])

[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]
 [13 14 15 16]
 [17 18 19 20]]
------------------------------
[ 6  7  8  9 10 11 12 13 14 15 16 17 18 19 20]

                        例2： 

a=np.arange(1,21).reshape(5,4)
print(a)
b=a<5
print(b)
print(a[b])


[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]
 [13 14 15 16]
 [17 18 19 20]]
------------------------------
[[ True  True  True  True]
 [False False False False]
 [False False False False]
 [False False False False]
 [False False False False]]
------------------------------
[1 2 3 4]

        (2)修改行或列

a=np.arange(1,21).reshape(5,4)
print(a)
a[:,2]=666 # 将所有行第三列改为666
print(a)

[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]
 [13 14 15 16]
 [17 18 19 20]]
------------------------------
[[  1   2 666   4]
 [  5   6 666   8]
 [  9  10 666  12]
 [ 13  14 666  16]
 [ 17  18 666  20]]

        对比，下面对某列满足条件的进行修改，采用链式法则的方式

a=np.arange(1,21).reshape(5,4)
print(a)
b=a[:,2]>5    # 判断3列中大于5的数
print(b)
a[:,2][b]=666    # 将3列先筛选出来，再筛选，修改
print(a)    

[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]
 [13 14 15 16]
 [17 18 19 20]]
------------------------------
[False  True  True  True  True]
------------------------------
[[  1   2   3   4]
 [  5   6 666   8]
 [  9  10 666  12]
 [ 13  14 666  16]
 [ 17  18 666  20]]

（四）数组索引

        还可以使用整数数组进行索引，如

        1.一维

a=np.arange(1,21,2)
print(a)
print(a[[2,3,5]])

[ 1  3  5  7  9 11 13 15 17 19]
[ 5  7 11]

        2.二维 

        一个数组返回的是行

a=np.arange(1,37).reshape(4,9)
print(a)
print('-'*30)
print(a[[1,3]]) # 返回的是行

[[ 1  2  3  4  5  6  7  8  9]
 [10 11 12 13 14 15 16 17 18]
 [19 20 21 22 23 24 25 26 27]
 [28 29 30 31 32 33 34 35 36]]
------------------------------
[[10 11 12 13 14 15 16 17 18]
 [28 29 30 31 32 33 34 35 36]]

         多个数组用逗号隔开，左行右列，返回返回的是一维对应元素

a=np.arange(1,17).reshape(4,4)
print(a)
print('-'*30)
print(a[[0,2],[1,3]])

[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]
 [13 14 15 16]]
------------------------------
[ 2 12]

        使用冒号的效果： 切片返回部分的二维数组

a=np.arange(1,17).reshape(4,4)
print(a)
print(a[0:3,[1,3]])    # 0列至2行的第1行与第3行
print(a[[0,3],1:3])    # 第0行与第3行的1列至3列


[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]
 [13 14 15 16]]
------------------------------
[[ 2  4]
 [ 6  8]
 [10 12]]
------------------------------
[[ 2  3]
 [14 15]]

三、基本操作

（一）运算

        数组与标量运算与矩阵相同，为每个元素与其进行计算，数组之间的运算先不做专门的探讨，此外，也可以使用相关函数进行计算

广播原则

        这里需要记录广播原则，进行数组计算时：

        当 a.shape=b.shape形状相同，a*b结果为对应位相乘

a=np.arange(1,10).reshape(3,3)
b=np.array(a)
print(a)
print(b)
print(a*b)

[[1 2 3]
 [4 5 6]
 [7 8 9]]
------------------------------
[[1 2 3]
 [4 5 6]
 [7 8 9]]
------------------------------
[[ 1  4  9]
 [16 25 36]
 [49 64 81]]

        在两形状不同时，以下两种情况可以进行数组计算：

        ①两数组形状不相等，但后缘维度（将维度进行右对齐，看末尾）轴长相同，如：

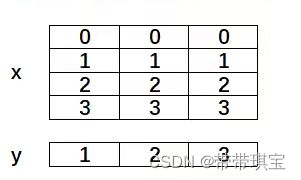
        x.shape 为 (4,3)，y.shape 为 (3,)，两者后缘维度都为3，所以可以进行计算，广播机制使数组向形状最长的看齐，即上面例子将这样进行计算：

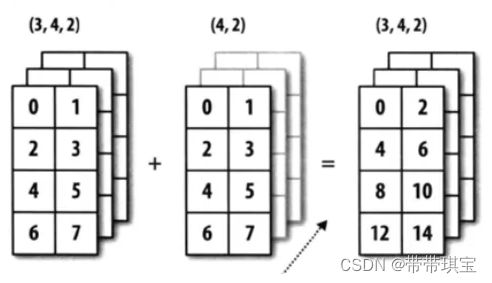
         三维数组也是同理，以下例子进行计算时将左边每一块都与右边进行相加，此外 (3,4,2) 与 (4,) 不可以进行计算，与 (4,1) 可以进行计算

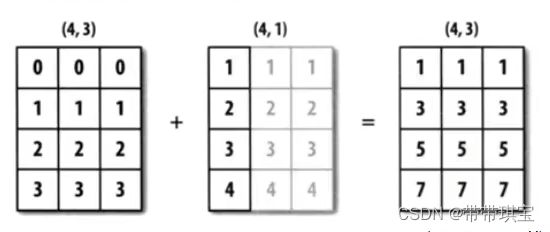
        ②其中一方后缘维度大小为1

        以下两个二维数组的形状：(4,3)与(4,1)

        尝试了一下三维的 (4,3,2) 与 (2,1) 、(3,) 不能进行计算，会报错，只能与 (3,1)、(3,2) 、(2,) 计算

        个人总结的可能不太准确，大概就是：将两个数组 shape 右对齐，对应位置的数组相等（最后一位可为1）即可进行计算。不同维度看后缘（是否相等或等于1），同维度必同长度，除非长为1 

（二）方法

        array.reshape(shape[,order])):返回重命名数组大小后的数组，不改变元素个数，也不改变原数组，相当于视图，shape为新数组的形状（a,b）a行b列；

        np.resize(a,new_shape):按照指定的结构（形状）改变数组，新数组若大于原数组，重新填充 a

a=np.array([(0,1),(2,3)])
b=np.resize(a,(3,3))
print(a)
print('-'*10)
print(b)

[[0 1]
 [2 3]]
----------
[[0 1 2]
 [3 0 1]
 [2 3 0]]
----------

        若是 array.resize(new_shape)，这种方法无返回值（因此不能赋值），用 0 填充； 

a=np.array([(0,1),(2,3)])
print(a)
print('-'*10)
a.resize((3,3),refcheck=False)
print(a)

[[0 1]
 [2 3]]
----------
[[0 1 2]
 [3 0 0]
 [0 0 0]]

        array.ravel(a[,order='C'/'F']):将任意形状的数组扁平化，返回 1 维数组的视图，当 order=‘F’ 时，可以按列依次读取排序。

1.拆分与合并：

        合并：append(arr，values，axis)：将值附加到数组的末尾，并返回 1 维数组。

                   stack(arrays, axis=0/1)（此外还有vstack、hstack、dstack）

a=np.arange(9).reshape(3,3)
b=np.arange(9).reshape(3,3)
print(a)
c=np.stack((a,b), axis=0)
d=np.stack((a,b), axis=1)
e=np.stack((a,b), axis=2)
print(c)
print(d)
print(e)

[[0 1 2]
 [3 4 5]
 [6 7 8]]
--------
[[[0 1 2]
  [3 4 5]
  [6 7 8]]

 [[0 1 2]
  [3 4 5]
  [6 7 8]]]
--------
[[[0 1 2]
  [0 1 2]]

 [[3 4 5]
  [3 4 5]]

 [[6 7 8]
  [6 7 8]]]
--------
[[[0 0]
  [1 1]
  [2 2]]

 [[3 3]
  [4 4]
  [5 5]]

 [[6 6]
  [7 7]
  [8 8]]]

        拆分：常使用split，或直接切片

2.其他方法

①等差

        linspace(start,stop,num,endpoint,restep,dtype)，得到等步长的数列

• start/stop/num：数列的首项、末项及个数
• endpoint：默认 True，包含末项
• restep：True 时显示间距，得到元组

a=np.linspace(1,5,5)
print(a)

[1. 2. 3. 4. 5.]

②等比

        logspace(start,stop,num,endpoint,base,dtype)，得到等步长的数列

• start/stop/num：数列的首项、末项及个数
• endpoint：默认 True，包含末项
• base：设置的底数，默认为10

a=np.logspace(1,5,5,base=2)
print(a)

[ 2.  4.  8. 16. 32.]

③改数据类型

        array.astype()

        原本数据类型不会改变

④统计量计算

        np.mean、np.min、np.std...等一系列统计指标计算

⑤条件计算

        np.where(条件，为真的值，非真的值)

        array.any()

        array.all()

⑥排序

        array.sort(axis,kind,order)：排序会修改原数组，多维数组默认按最后的轴排序

        np.argsort(array,axis,kind,order)：与sort类似，但返回的是升序排序后的索引，降序使用-array即可

⑦去重

        np.unique(array)：对array去重

        np.in1d(array1,array2)：检查1的元素是否在2中存在，返回与1相同的布尔数组

（三）拷贝

        1.浅拷贝

        a=b，a 与 b 共同指向同一内存地址，值相同会相互影响

        a=b[:]也是

        2.深拷贝

        a=b.copy()：互不影响，开辟了新的内存空间给 a