【数据结构】二叉树的前、中、后序、深度、广度遍历(图、文、代码)
文章目录
- 前言
- 一、二叉树
- 二、二叉树结构定义
- 三、二叉树遍历
-
- 前序遍历(先序遍历)
-
- 代码递归实现
- 代码非递归实现
- 中序遍历
-
- 代码递归实现
- 代码非递归实现
- 后序遍历(难点)
-
- 递归代码实现
- 非递归代码实现
- 广度优先遍历(BFS)(层次遍历)
-
- 代码实现
- 深度优先遍历(DFS)
前言
重新复习了一遍数据结构的二叉树,发现了还有很多不理解的地方,重新梳理一番。有不理解的欢迎评论区讨论。
一、二叉树
二叉树(Binary tree)是一种树形结构,其特点是每个结点至多只有两棵子树(即二叉树中不存在度大于2的结点),并且二叉树的子树有左右之分,其次序不能颠倒。
二、二叉树结构定义
不过多讲解了,主要为了方便读者进行自行实现
static class TreeNode {
Integer val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(Integer val) { this.val = val; }
TreeNode(Integer val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
三、二叉树遍历
前序遍历(先序遍历)
前序遍历的思想很简单,利用递归的思想,二叉树非空的情况下,操作过程如下:
(1)访问根节点
(2)先序遍历左子树【递归】
(3)先序遍历右子树【递归】
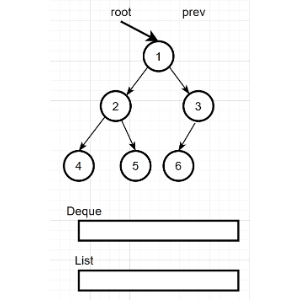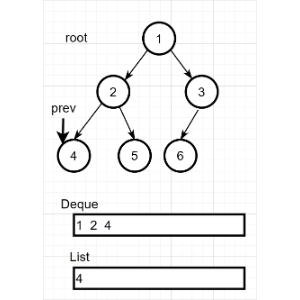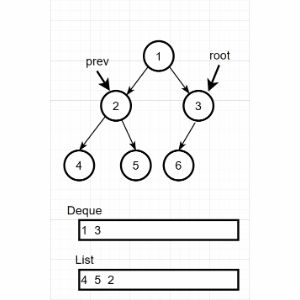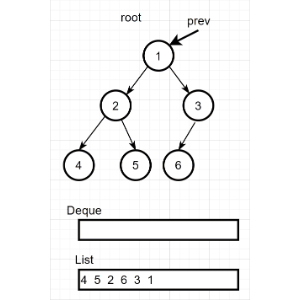
下面结合图片来讲解,以下是配合说明的二叉树示例:
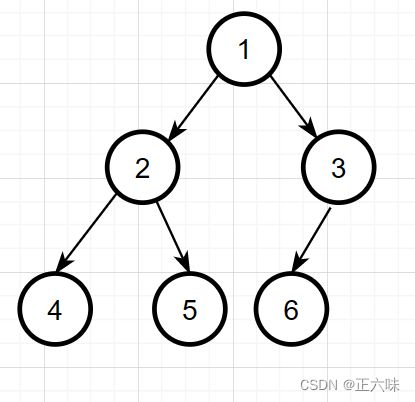
前序遍历的具体过程:
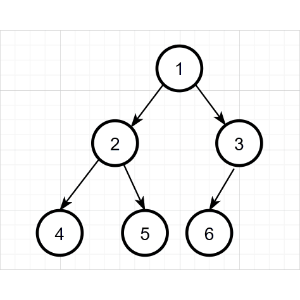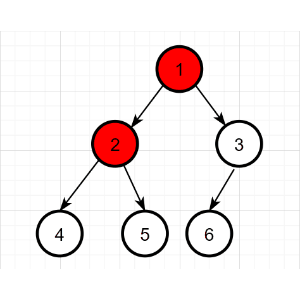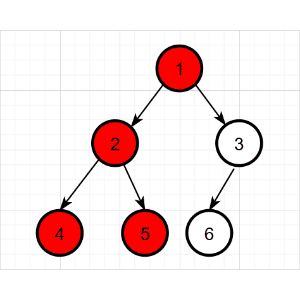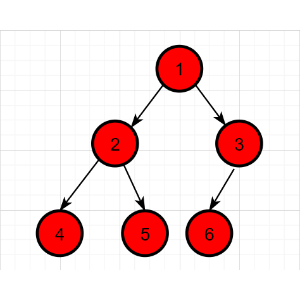
先序遍历结果为:1 2 4 5 3 6
代码递归实现
/**
* 前序遍历递归遍历二叉树
* @param listTree
* @param node
*/
public static void pre(List listTree,TreeNode node){
//设置递归结束条件
//判断结点是否为空
if (node == null) return; //若为空则结束本次递归
listTree.add(node.val); //输出根节点
pre(listTree,node.left); //遍历左子树
pre(listTree,node.right); //遍历右子树
}
代码非递归实现
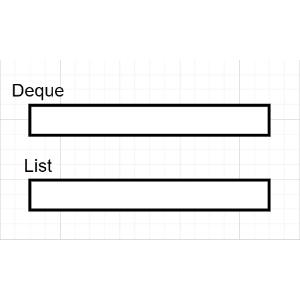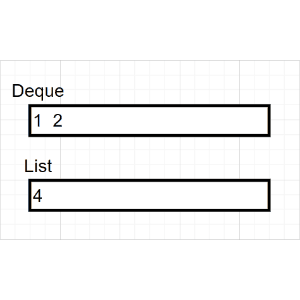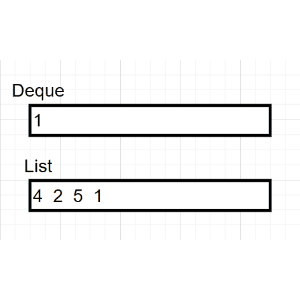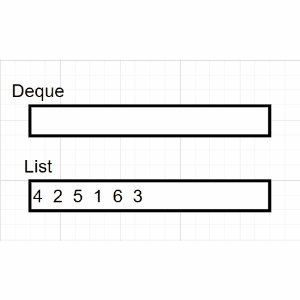
非递归代码的实现需要借助栈的先进后出(FILO)的思想,具体过程描述如下:
(1)判断当前结点是否为空
(2)如果当前结点非空,保存节点(输出),并入栈
(2)在(1)的基础上,沿着根的左孩子继续回到(1)判断
(3)如果当前结点为空,弹出栈顶元素,沿着栈顶元素的右孩子继续回到(1)判断
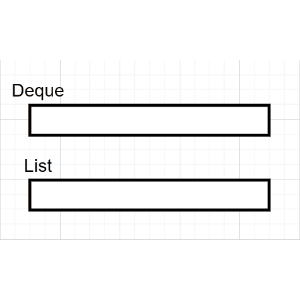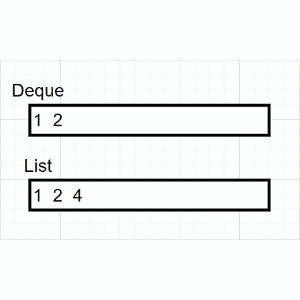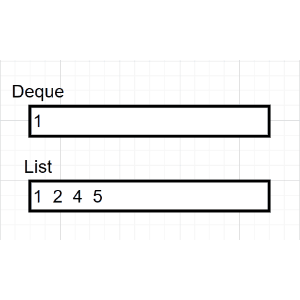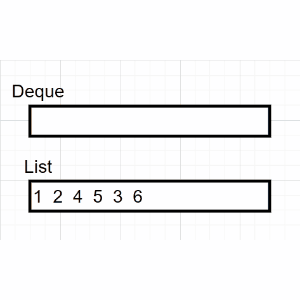
/**
* 前序遍历
* @param root
* @return
*/
public static List<Integer> pre_order(TreeNode root){
List<Integer> listTree = new ArrayList<>();
//创建队列作为树节点的临时存储
Deque<TreeNode> deque = new LinkedList<>();
//模拟递归过程
while(root != null || !deque.isEmpty()){
//如果根节点为空
if (root != null){
listTree.add(root.val); //保存根节点
deque.push(root); //根节点存入栈中
root = root.left; //往左子树走
}else {
//根节点为空
//弹出栈顶元素
root = deque.pop().right; //往右子树走
}
}
return listTree;
}
中序遍历
中序遍历与前序遍历类似,利用递归的思想,二叉树非空的情况下,操作过程如下:
(1)先序遍历左子树【递归】
(2)访问根节点
(3)先序遍历右子树【递归】
采用说明的二叉树示例同上,具体过程如下:
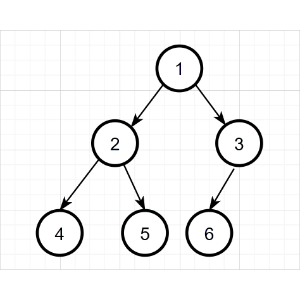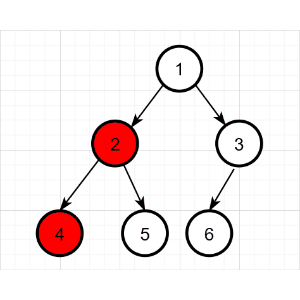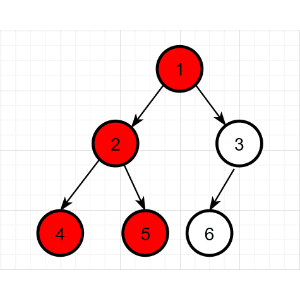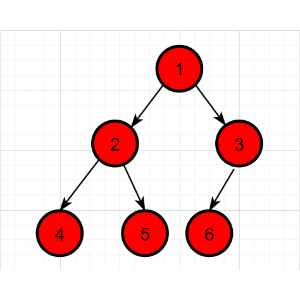
中序遍历结果为:4 2 5 1 6 3
代码递归实现
/**
* 中序遍历递归遍历二叉树
* @param listTree
* @param node
*/
public static void mid(List listTree,TreeNode node){
//设置递归结束条件
//判断结点是否为空
//若为空则结束本次递归
if (node == null) return;
mid(listTree,node.left); //遍历左子树
listTree.add(node.val); //输出根节点
mid(listTree,node.right); //遍历右子树
}
代码非递归实现
实现步骤跟前序遍历基本一致,具体过程描述如下:
(1)判断当前结点是否为空
(2)如果当前结点非空,当前结点入栈
(3)在(1)的基础上,沿着根的左孩子继续回到(1)判断
(4)如果当前结点为空,弹出栈顶元素,保存该节点
(5)沿着栈顶元素的右孩子继续回到(1)判断
/**
* 中序遍历二叉树
* @param root 二叉树根节点
* @return
*/
public static List<Integer> middle_order(TreeNode root){
List<Integer> listTree = new ArrayList<>();
//创建队列作为树节点的临时存储
Deque<TreeNode> deque = new LinkedList<>();
//迭代结束条件 树队列非空
while (root != null || !deque.isEmpty()){
//中序遍历
//模拟递归的过程
//如果根节点非空 则进行递归
if (root != null){
deque.push(root); //根节点存入栈中
root = root.left; //往左子树走
}else{
//结点为空 表示左子树走到头了
root = deque.pop(); //弹出结点
listTree.add(root.val); //保存结点
root = root.right; //走右子树
}
}
return listTree;
}
后序遍历(难点)
后序遍历在理解上不难,但在非递归的实现上与前序遍历和中序遍历有些差别。
利用递归的思想,二叉树非空的情况下,操作过程如下:
(1)先序遍历左子树【递归】
(2)先序遍历右子树【递归】
(3)访问根节点
采用说明的二叉树示例同上,具体过程如下:
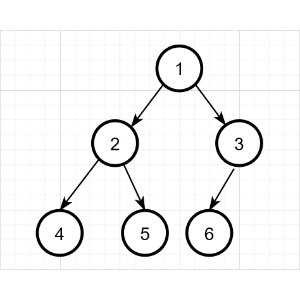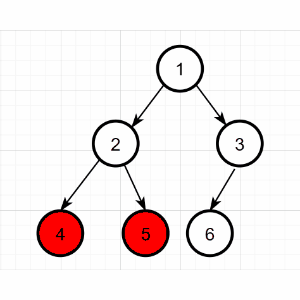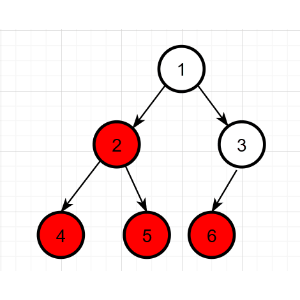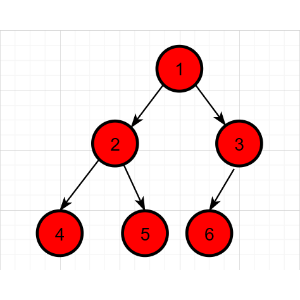
后序遍历序列:4 5 2 6 3 1
递归代码实现
/**
* 后序遍历递归遍历二叉树
* @param listTree
* @param node
*/
public static void post(List listTree,TreeNode node){
//设置递归结束条件
//判断结点是否为空
//若为空则结束本次递归
if (node == null) return;
post(listTree,node.left); //遍历左子树
post(listTree,node.right); //遍历右子树
listTree.add(node.val); //输出根节点
}
非递归代码实现
后序遍历的非递归代码实现是最难的。因为后序遍历中,要保证左右孩子都已被访问,并且左孩子在右孩子前访问才能访问根节点。所以必须设定一个辅助指针,指向最近访问过的结点(也可以在结点中添加标志域,记录是否被访问过)
具体实现步骤:
(1)判断当前结点是否为空
(2)如果当前结点非空,当前结点入栈
(3)在(1)的基础上,沿着根的左孩子继续回到(1)判断
(4)如果当前结点为空,获得栈顶元素(不出栈)
(5)判断栈顶元素的右孩子是否为空或者右孩子是否被访问过
(6)如果(5)判断为真,弹出栈顶元素,保存该节点;同时记录该节点,记录为最近访问过的结点,并将根节点指针置空,继续循环判断
(7)如果(5)判断为假,沿着根的右孩子继续回到(1)判断
/**
* 后序遍历
* @param root
* @return
*/
public static List<Integer> post_order(TreeNode root){
List<Integer> listTree = new ArrayList<>();
//创建队列作为树节点的临时存储
Deque<TreeNode> deque = new LinkedList<>();
TreeNode prev = null; //暂存前一个结点
while (root != null || !deque.isEmpty()){
//模拟递归过程
//判断当前结点是否为空
if (root != null){
deque.push(root); //根节点存入栈中
root = root.left; //往左子树走
}else {
root = deque.getFirst(); //获取最后一个结点 但不出栈
if (root.right == null || root.right == prev){ //如果右子树为空或被访问过
deque.pop(); //弹出栈顶结点
listTree.add(root.val); //保存结点
prev = root; //记录当前结点
root = null; //重置结点 相当于遍历完已该节点为根的子树,将根节点置空
}else {
root = root.right;
}
}
}
return listTree;
}
广度优先遍历(BFS)(层次遍历)
二叉树的层次遍历,即按着箭头所指方向,按照1,2,3的层次顺序,对二叉树的各个节点进行访问。
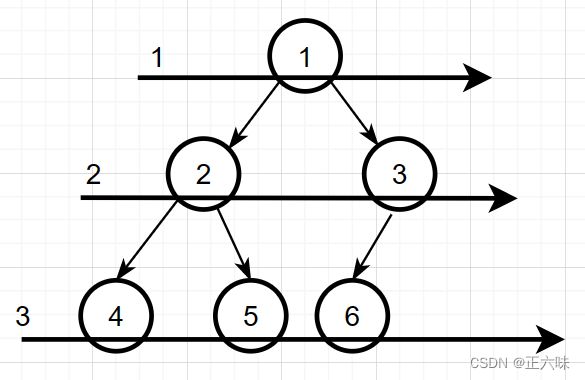
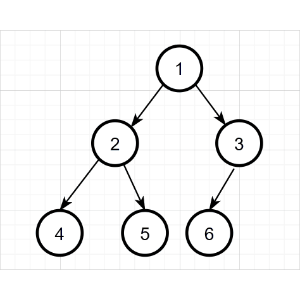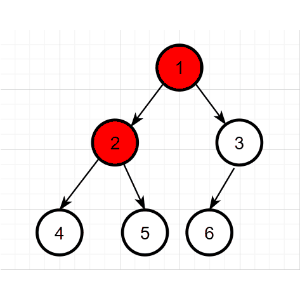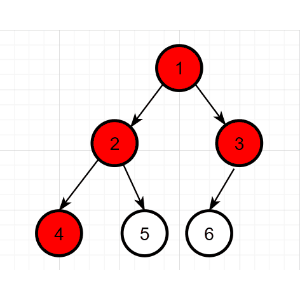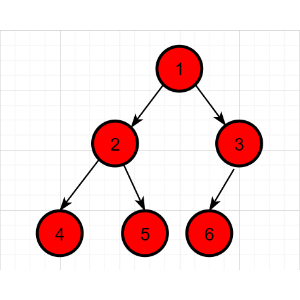
层次遍历序列:1 2 3 4 5 6
代码实现
借助一个队列,先将根节点入队。进入循环,获得队头元素(出队),访问出队节点的左孩子,左孩子非空,将左孩子进入队列;访问出对节点的右孩子,右孩子非空,将右孩子进入队列。如此反复,直到队列为空。
/**
* 广度遍历
* @param root
* @return
*/
public static void bfs(TreeNode root){
//初始化辅助队列
Queue<TreeNode> bfsQueue = new LinkedList<>();
bfsQueue.offer(root);
while (!bfsQueue.isEmpty()){ //队列非空
root = bfsQueue.poll(); //获得队列的第一个结点
System.out.print(root.val + " "); //进行输出
if (root.left != null){ //如果该节点的左孩子非空
bfsQueue.offer(root.left); //进入队列
}
if (root.right != null){ //如果该节点的右孩子非空
bfsQueue.offer(root.right); //进入队列
}
}
}
深度优先遍历(DFS)
深度优先遍历其实就是前、中、后序遍历,不再赘述。