Java中树的遍历

---

前言

在编程语言数据结构中，树是非常重要且应用较为频繁的一种，此文章主要讲述了在Java中，对二叉树进行遍历。

---

一、树的定义

树是一种数据结构，它是由n(n≥0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：
每个节点有零个或多个子节点；没有父节点的节点称为根节点；每一个非根节点有且只有一个父节点；除了根节点外，每个子节点可以分为多个不相交的子树。¹

二、树的种类

• 无序树：树中任意节点的子结点之间没有顺序关系，这种树称为无序树,也称为自由树；
• 有序树：树中任意节点的子结点之间有顺序关系，这种树称为有序树；
• 二叉树：每个节点最多含有两个子树的树称为二叉树；
• 满二叉树：叶节点除外的所有节点均含有两个子树的树被称为满二叉树；
• 完全二叉树：除最后一层外，所有层都是满节点，且最后一层缺右边连续节点的二叉树称为完全二叉树；
• 哈夫曼树（最优二叉树）：带权路径最短的二叉树称为哈夫曼树或最优二叉树。

三、二叉树的遍历

话不不多先上个图(画的有些粗糙)

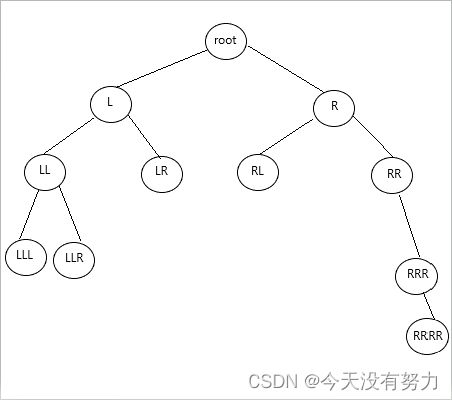
然后使用java语言，构造一个树的结构

	// 定义一个类
	@Getter
    @Setter
    @ToString
    @RequiredArgsConstructor
    public class Tree {
        private final String id;
        private final String parentId;
        private Tree leftLeaf;
        private Tree rightLeaf;
        private final boolean left;
    }

// 开始构建树结构，此处省略类定义，直接上方法
public static void main(String[] args) {
        Tree root = new Tree("root", null, false);
        Tree rootL = new Tree("rootL", "root", true);
        Tree rootR = new Tree("rootR", "root", false);
        Tree rootLL = new Tree("rootLL", "rootL", true);
        Tree rootLR = new Tree("rootLR", "rootL", false);
        Tree rootRL = new Tree("rootRL", "rootR", true);
        Tree rootRR = new Tree("rootRR", "rootR", false);
        Tree rootLLL = new Tree("rootLLL", "rootLL", true);
        Tree rootLLR = new Tree("rootLLR", "rootLL", false);
        Tree rootRRR = new Tree("rootRRR", "rootRR", false);
        Tree rootRRRR = new Tree("rootRRRR", "rootRRR", false);
        List trees = Arrays
                .asList(rootL, rootR, rootLL, rootLR, rootRL, rootRR, rootLLL, rootLLR, rootRRR, rootRRRR);
        buildTree(root, trees);
    }

	/**
     * 构建二叉树结构
     * @param parent 父节点
     * @param treeList 树节点的集合
     */
    private static void buildTree(Tree parent, List treeList) {
        if (parent != null) {
            String pId = parent.getId();
            List child = treeList.stream()
                    .filter(tree -> tree.getParentId().equals(pId)).collect(Collectors.toList());
            if (!child.isEmpty()) {
                child.forEach(tree -> {
                    if (tree.isLeft()) {
                        parent.setLeftLeaf(tree);
                    } else {
                        parent.setRightLeaf(tree);
                    }
                });
            }
            buildTree(parent.getLeftLeaf(), treeList);
            buildTree(parent.getRightLeaf(), treeList);
        }
    }

一、深度优先遍历（DFS）

先访问树的根节点，然后左节点，一直往下访问左节点，直到最左侧节点没有子节点的时候，往上退一步到当前左节点的父节点，然后此父节点的右子节点又重复以上步骤
所以上图的访问顺序为
root->L->LL->LLL->LLR->LR->R->RL->RR->RRR->RRRR

	/**
     * 深度优先遍历
     * @param root 根节点
     * @return 按照遍历顺序排列的集合
     */
    private static List depthErgodic(Tree root) {
        List result = new ArrayList<>(11);
        Stack stack = new Stack<>();
        Tree head;
        stack.add(root);
        while (!stack.isEmpty() && (head = stack.pop()) != null) {
            if (head.getRightLeaf() != null)
                stack.add(head.getRightLeaf());
            if (head.getLeftLeaf() != null)
                stack.add(head.getLeftLeaf());
            result.add(head.getId());
        }
        return result;
    }

二、广度优先遍历（BFS）

横向从左到右 一层一层的往下访问
所以上图的访问顺序为
root->L->R->LL->LR->RL->RR->LLL->LLR->RRR->RRRR

	/**
     * 广度优先遍历
     * @param root 根节点
     * @return 按照遍历顺序排列的集合
     */
    private static List spanErgodic(Tree root) {
        List result = new ArrayList<>(11);
        Queue treeQueue = new LinkedList<>();
        Tree head;
        treeQueue.offer(root);
        while ((!treeQueue.isEmpty()) && (head = treeQueue.poll()) != null) {
            if (head.getLeftLeaf() != null)
                treeQueue.offer(head.getLeftLeaf());
            if (head.getRightLeaf() != null)
                treeQueue.offer(head.getRightLeaf());
            result.add(head.getId());
        }
        return result;
    }

---

总结

二叉树还有很多其他的遍历方法，这里只是指出了最常用的两种。

---

1. https://baike.baidu.com/item/%E6%A0%91/2699484?fr=aladdin ↩︎