VINS-Mono-后端优化 （三：视觉雅可比推导）

用逆深度是因为这样可以在优化中从优化3个变量降低到1个，降低优化的维度加快求解速度
用逆深度是因为当距离很远的时候，$\frac{1}{x}$ $x$ 就会无穷大，而3D点很近的情况也一般不会有，这也是为了数值稳定性

用逆深度的话就要和其中一帧进行绑定，这个就是和观测到该点的第一帧进行绑定，这样才能表示一个3D点信息

划窗中维护的全部都是IMU下的位姿，所以相机要通过外参变换到IMU坐标系下

这里就构成了视觉误差，需要求关于优化变量的雅可比矩阵，这里约束了第 $i$ 帧和第 $j$ 帧的 IMU 的姿态，同时还会优化相机和IMU的外参，这个也是紧耦合的特点之一（上一节同时优化 IMU预积分自身的零偏Ba也是紧耦合特点之一），3D点（逆深度）也是要优化，总共就是4个参数

转换公式如下：
第 $i$ 帧归一化坐标系 -> 第 $j$ 帧相机系，$\frac{1}{\lambda }$，就是深度，$\lambda$ 是逆深度

将旋转和平移分开后如下：

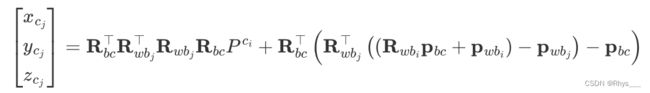
将刚刚第 $i$ 帧相机系下的3D点进行归一化，然后和光流追踪到的匹配点进行残差计算，这就获得了视觉重投影误差

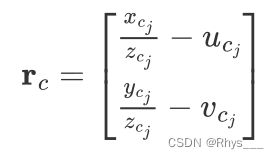
计算残差对优化量的雅可比

有带时间延时估计的雅可比计算和不带时间估计的雅可比计算
这里先讲不带时间延时的雅可比计算

这里的误差项是2维的，坐标点是3维的
要求误差对旋转的雅可比只能通过链式求导的方式
$\frac{\partial r}{\partial p_j}\cdot \frac{\partial p_j}{\partial x}$

$\frac{\partial r}{\partial p_j}$ 是2×3维的，对平移 $x,y,z$ 进行求导
$=\left[\begin{array}{ccc}\frac{1}{z}& 0& -\frac{x}{z^2}\\ 0& \frac{1}{z}& -\frac{y}{z^2}\end{array}\right]$

这里的误差也有协方差矩阵，提点的置信度是设定为1.5个像素不变
残差也得乘上置信度

计算 $p_j$ 对 $T$ 的雅可比

平移 $x,y,z$ 的公式为

$T$ 包含旋转 $R$ 和平移 $t$

对 $i$ 时刻求导

$i$ 时刻的变量也是要优化的量，所以当然也要求导

对 $p_{w{b}_i}$ 求导

$\frac{\partial p_j}{\partial p_{w{b}_i}}=R_{bc}^T\cdot R_{w{b}_j}^T$

对 $R_{w{b}_i}$ 求导

$\frac{\partial p_j}{\partial R_{w{b}_i}}$
先把公式中有 $R_{w{b}_i}$ 的项提取出来

$=R_{bc}^T{R}_{w{b}_j}^T{R}_{w{b}_i}(R_{bc}{P}^{c_i}+p_{bc})$
$=A{R}_{w{b}_i}b$

后面那一串 $b$ 乘完后是向量，所以可以对李代数进行扰动求导（纯旋转矩阵是不能对李代数求导的，因为矩阵无法对向量求导，这里是乘完后是个向量，所以可以用向量来表示旋转的扰动量，然后用导数的定义来进行求导）

$\frac{\partial A{R}_{w{b}_i}b}{\partial \varphi }=\frac{A{R}_{w{b}_i}exp({\varphi }^{\wedge })b-A{R}_{w{b}_i}b}{\varphi }$
$=\frac{A{R}_{w{b}_i}(I+{\varphi }^{\wedge })b-A{R}_{w{b}_i}b}{\varphi }$
$=\frac{A{R}_{w{b}_i}{\varphi }^{\wedge }b}{\varphi }$
根据反对成矩阵的性质
$=\frac{-A{R}_{w{b}_i}{b}^{\wedge }\varphi }{\varphi }$
$=-A{R}_{w{b}_i}{b}^{\wedge }$

那个信息矩阵乘完第一步也得乘进来这里这个第2步的雅可比矩阵

对 $j$ 时刻进行求导

对 $p_{w{b}_j}$ 求导

$\frac{\partial p_j}{\partial p_{w{b}_j}}=-R_{bc}^T\cdot R_{w{b}_j}^T$

对 $R_{w{b}_j}$ 求导

把和 $R_{w{b}_j}$ 有关的项提取出来
$=R_{bc}^T{R}_{w{b}_j}^T(R_{w{b}_i}{R}_{bc}{P}^{c_i}+R_{w{b}_i}{p}_{bc}+p_{w{b}_i}-p_{w{b}_j})$
$=A{R}_{w{b}_j}^{T}b$

对 $R_{w{b}_j}^T$ 是只能左乘的，但是我们现在要算他右乘的扰动方向，因为方向会不同，用左乘的求导结果加个负号就是右乘的结果，这里推导直接用右乘，所以要加个逆把这个转置消掉来进行推导
$=A(R_{w{b}_j}exp({\varphi }^{\wedge }){)}^{-1}b-A(R_{w{b}_j}{)}^{-1}b$
$=A(I-{\varphi }^{\wedge })R_{w{b}_j}^{T}b-A(R_{w{b}_j}{)}^{-1}b$
$=-A{\varphi }^{\wedge }{R}_{w{b}_j}^{T}b$
$=A(R_{w{b}_j}^{T}b{)}^{\wedge }\varphi$
消去 $\varphi$
$=A(R_{w{b}_j}^{T}b{)}^{\wedge }$

后面的 $R_{w{b}_j}^{T}b$ 实际就是 3D 点在 第 $j$ 帧 IMU系下的位姿，按照展开前的刚体变换来理解一下就好了

对 IMU-相机 的外参求导$

对 $p_{bc}$ 求导

$=R_{bc}^T{R}_{w{b}_j}^T{R}_{w{b}_i}-R_{bc}^T$

对 $R_{bc}$ 求导

代码中的 $ric=R_{bc},tic=t_{bc}$，$Q=R_{wb}$

导数是符合加法的 $(f(x)+g(x){)}^{{}^{\prime }}=f^{{}^{\prime }}(x)+g^{{}^{\prime }}(x)$

加法后面的求导结果 $=(R_{bc}^{T}b)$ ，这个推导和上面类似，就不详细写了

加法前面的求导稍微复杂一点
$=(R_{bc}exp({\varphi }^{\wedge }){)}^{-1}{R}_{w{b}_j}^T{R}_{w{b}_i}{R}_{bc}^{T}exp({\varphi }^{\wedge })P^{c_i}-R_{bc}^T{R}_{w{b}_j}^T{R}_{w{b}_i}{R}_{bc}^T{P}^{c_i}$

下面暂时省略写后面它自身

$=(I-{\varphi }^{\wedge })R_{bc}^T{R}_{w{b}_j}^T{R}_{w{b}_i}{R}_{bc}^T(I+{\varphi }^{\wedge })P^{c_i}$
$=(I-{\varphi }^{\wedge })A(I+{\varphi }^{\wedge })P^{c_i}$
$=(A-{\varphi }^{\wedge }A)(I+{\varphi }^{\wedge })P^{c_i}$
$=(A+A{\varphi }^{\wedge }-{\varphi }^{\wedge }A-{\varphi }^{\wedge }A{\varphi }^{\wedge })P^{c_i}-A{P}^{c_i}$

其中 ${\varphi }^{\wedge }A{\varphi }^{\wedge }$ 是二阶，是相对于一阶的无穷小，这里只讨论一阶的展开且 $\varphi$ 本身就是小量，所以直接约掉

$=(A{\varphi }^{\wedge }-{\varphi }^{\wedge }A)\cdot P^{c_i}$
$=-A{P}^{\wedge }\varphi +(AP{)}^{\wedge }\varphi$
约掉 $\varphi$
$=-A{P}^{\wedge }+(AP{)}^{\wedge }$

对逆深度 $\lambda$ 求导

$\frac{\partial p_j}{\partial P^{c_i}}\frac{\partial P^{c_i}}{\partial \lambda }$

前面的 $\frac{\partial p_j}{\partial P^{c_i}}=R_{bc}^T{R}_{w{b}_j}^T{R}_{w{b}_i}{R}_{bc}$

$P^{c_i}=\frac{1}{\lambda }\cdot p$，$p$ 是归一化相机系下的3D点

$\frac{\partial P^{c_i}}{\partial \lambda }=-\frac{1}{{\lambda }^2}\cdot p$

这个 $-\frac{1}{{\lambda }^2}$ 是个系数，移到哪里都可以

零空间漂移处理

优化的时候会固定滑窗中的第一帧的xyz和yaw角，因为IMU约束的是相对位姿，且IMU的4个不可观自由度就是 $yaw、x、y、z$，绝对位姿是没有约束的，所以可能会产生在 4自由度的 0 空间漂移的情况，fusion中的GPS就是约束绝对位姿的。

VINS中的固定是先计算第一帧的yaw和xyz的偏移量，然后把后面的帧都减去这个偏移量，偏移回之前的位置，这样的做法就类似ORB中的固定第一帧的位姿，不过这里是减去第一帧的偏移量，其实就是滑窗中的整条轨迹调整回偏移前的位置，这样就保证不受 0 空间的影响。

和 yaw相关的量都会受影响，就是和旋转向量的量都会受影响，$P,V$ 受影响，零偏 $Ba,Bg$ ，外参 $Tbc$ 不受影响

前面会把旋转矩阵变成rpy，然后把yaw的角度差取出来构成新的偏移旋转矩阵，因为只是yaw发生漂移