数据查找(search)-----散列表(哈希表)
目录
前言
一.散列表(哈希表)基本概念
二.哈希函数的构造
构造原则
构造方法
1.直接定址法
2.除留余数法
3.数字分析法
三.地址冲突
四.处理冲突的方法
开放定址法
1.线性探测法
2.二次探测法
3.伪随机探测法
链地址法
五.散列表的查找
前言
今天我们学习一种新的数据查找表----散列表,也叫做哈希表,散列表是作为一种高效的查找表,储存数据的引索,然后通过这个引索来找到这个数据,下面就一起来看看。
一.散列表(哈希表)基本概念
散列表(Hash table,也叫哈希表),是根据关键码值(Key value)而直接进行访问的数据结构。 也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。 这个映射函数叫做散列函数,存放记录的数组叫做散列表。
哈希表就是将数据以他的特征信息为标准,存在一块空间中,当我们要查询某数据时,我们就可以通过该数据的特征信息快速锁定到该数据的位置,从而大大的提高了数据的查询速度。
二.哈希函数的构造
散列表的基本思想:记录的存储位置与关键字之间存在对应关系
散列表就是去通过一个函数关系实现关键字和位置引索的转换。这里叫做散列方法,其概念如下
散列方法(杂凑法)依该函数按关键字计算元素的存储位置选取某个函数并按此存放查找时,由同一个函数对给定值k计算地址,将k与地址单元中元素关键码进行比,确定查找是否成功。
散列函数(杂凑函数): 散列方法中使用的转换函数,函数式即: H(key)=index;
构造原则
哈希函数构造的时候要去考虑以下这些因素:
- 执行速度(即计算散列函数所需时间)
- 关键字的长度
- 散列表的大小
- 关键字的分布情况
- 查找频率。
原则一:所选函数对关键码计算出的地址,应在散列地址集中致均匀分布,以减少空间浪费
所以对于一个哈希函数,不同的key键值进行转换的时候有可能会出现结果一样,也就是储存的地址发生了冲突,所以对于一个哈希函数要进行恰当选取,尽量散列地址集中均匀分布,可以减少地址冲突的情况,同时还可以减少空间的浪费。
原则二:所选函数尽可能简单,以便提高转换速度
这个就没什么好讲的了,对于一个哈希函数,一般来说我们能简单计算就简单计算,不仅计算机好理解我们自己也好理解。
总而言之构造哈希函数的时候最好根据元素集合的特性构造,满足以下两点要求:
- 要求一: n个数据原仅占用n个地址虽然散列查找是以空间换时间,但仍希望散列的地址空间尽量小.
- 要求二:无论用什么方法存储,目的都是尽量均匀地存放元素,以避免冲突。
构造方法
1.直接定址法
函数式:
Hash(key) = a*key + b (a、b为常数)
优缺点分析:
- 优点: 以关键码key的某个线性函数值为散列地址,不会产生冲突.
- 缺点:要占用连续地址空间,空间效率低
2.除留余数法
函数式:
Hash(key)= key mod p (p是一个整数)
//散列表函数(哈希函数)
int Hash(int key, int tablesize) {
return key % tablesize;
}关键: 如何选取合适的p?
技巧: 设表长为m,取 pm 且为质数
这种方法是哈希函数最常用的方法,其计算简单,求得的结果分布也比较分散,下面我会以这种方式为示例进行代码是书写。
3.数字分析法
假设关键字是以r为基的数(如:以10为基的十进制数),并且哈希表中可能出现的关键字都是事先知道的,则可取关键字的若干数位组成哈希地址。
例如有80个记录,其关键字为8位十进制数。假设哈希表的表长为100%,则可取两位十进制数组成哈希地址。'取哪两位?原则是使得到的哈希地址尽量避免产生冲突,则需从分析这80个关键字着手。假设这80个关键字中的一部分如下所列:
对关键字全体的分析中我们发现:第①②位都是“8 1”,第③位只可能取1、2、3或4,第⑧位只可能取2,5或7,因此这4位都不可取。由于中间的4位可看成是近乎随机的,因此可取其中任意两位,或取其中两位与另外两位的叠加求和后舍去进位作为哈希地址。
三.地址冲突
冲突 :不同的关键码映射到同一个散列地址
key1 != key2,但是H(key1)=H(key2)
好了,现在问题来了,如果不同的key值,经过哈希函数计算出来的地址相同怎么办?也就是地址冲突如何去处理呢?总不可能同一个地址储存两个不同的数据吧?别急,下面接着看。
四.处理冲突的方法
对于上面地址出现冲突我们有相对于的处理方法,下面我就详细介绍两种最常用的方法,当然还有很多种,但是大家可以根据自己的要求去拓展学习。
开放定址法
开放定址法是对于顺序存储结构的散列表进行地址冲突的处理,这个方法就是对当前键值key进行地址的试探然后根据试探的结果进行进一步处理,其下还有三种探测方法,分别是线性探测法、二次探测法、伪随机探测法。
基本思想 :有冲突时就去寻找下一个空的散列地址,只要散列表足够大,空的散列地址总能找到,并将数据元素存入。
1.线性探测法
探测公式: Hi=(Hash(key)+di) mod m ( 1
其中: m为散列表长度
di为增量序列 1,2,...m-1,且di=i(一旦冲突,就找下一个地址,直到找到空地址存入)
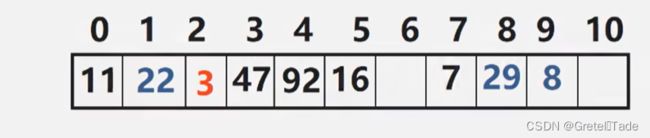
例:关键码集为 {47,7,29,11,16,92,22,8,3} ,散列表的长度为m=11;散列函数为Hash(key)=key mod 11,拟用线性探测地址冲突。建散列表如下:
解释:
- 47、7均是由散列函数得到的没有冲突的散列地址
- Hash(29)=7,散列地址有冲突,需寻找下一个空的散列地址:由H=(Hash(29)+1) mod 11=8,散列地址8为空,因此将29存入。
- 11、16、92均是由散列函数得到的没有冲突的散列地址;
- 另外,22、8、3同样在散列地址上有冲突,也是由H1,找到空的散列地址的。
代码写法:
#include
#include
#include
#include
//节点数据
typedef struct data {
int key;//键值,关键字
char id[10];//其他数据
}Datatype;
//表结果
typedef struct list {
Datatype* data;
int tablesize;//表长度
}Table;
//散列表函数(哈希函数)
int Hash(int key, int tablesize) {
return key % tablesize;
}
//创建空哈希表
Table* create_nulltable(int size) {
if (size == 0) {
printf("size is 0\n");
return NULL;
}
Table* T = (Table*)malloc(sizeof(Table));
if (!T) {
printf("ERROR\n");
exit(-1);
}
T->data = (Datatype*)malloc(sizeof(Datatype)*size);
if (!T->data) {
printf("ERROR\n");
exit(-1);
}
T->tablesize = size;
return T;
}
//创建初始化表
Table* create_inittable(int size) {
Table* T = create_nulltable(size);
for (int i = 0; i < T->tablesize; i++) {
T->data[i].key = -1;//键值初始化为-1,表示未储存数据
strcpy(T->data[i].id, "");//初始化为空字符串
}
return T;
}
//插入元素
void insert_data(Table* T, Datatype data) {
assert(T);
int index = Hash(data.key, T->tablesize);
//01--直接插入
if (T->data[index].key == -1) {
T->data[index] = data;
}
//02--已经被占用了,往后找
else {
while (T->data[index].key != -1) {
index++;
}
//找到了这个位置,插入
T->data[index] = data;
}
}
//查找元素(线性)
Datatype search_data(int key, Table* T) {
int loca = Hash(key, T->tablesize);//定位
//如果当前位置的key值就是想要找的key值,就直接返回
if (T->data[loca].key == key) {
printf("Found it\n");
return T->data[loca];
}
//如果当前key值不是要找的key值,就往后找
else {
while (T->data[loca].key != key) {
loca++;
if (T->data[loca].key == key) {
printf("Found it\n");
return T->data[loca];
}
}
}
printf("Didn't find\n");
}
//散列表删除元素
void delete_data(int key ,Table* T) {
assert(T);
//找到这个元素
Datatype target = search_data(key, T);
int loca = target.key;
//删除操作
T->data[loca].key = -1;
strcpy(T->data[loca].id, "");
}
//输出散列表
void print(Table* T) {
printf("table size: %d\n", T->tablesize);
for (int i = 0; i < T->tablesize; i++) {
//键值 对
printf("%d: %s\n", T->data[i].key, T->data[i].id);
}
} 2.二次探测法
二次探测法
关键码集为{47,7,29,11,16,92,22,8,3}散列函数为: Hash(key)=key mod 11
设:Hi=(Hash(key)+d)mod m其中:
m为散列表长度,m要求是某个4k+3的质数
di为增量序列 1^2,-1^2,2^2,-2^2,...,q^2
Hash(3)=3,散列地址冲突,由H1=(Hash(3)+1^2) mod 11=4仍然冲突,H2=(Hash(3)-1^2) mod 11=2找到空的散列地址,存入。
插入和查找代码如下:
//插入元素(二次探测)
void insert_data(Table* T, Datatype data) {
assert(T);
int index = Hash(data.key, T->tablesize);
//01--直接插入
if (T->data[index].key == -1) {
T->data[index] = data;
}
//02--已经被占用了,往后找
else {
int i = 1;
int k = index;
while (T->data[k].key != -1) {
k = index + i * i * pow(-1, i - 1);
//如果此时的k<0 的话是不能储存的,所以要跳过这一步,进入下一个预选位置
if (k < 0) {
while (k < 0) {
i++;
k = index + i * i * pow(-1, i - 1);
}
//循环出来后k是>0的
}
else
i++;
}
//找到了这个位置,插入
T->data[k] = data;
}
}
//查找元素(二次探测)
Datatype search_data(int key, Table* T) {
int loca = Hash(key, T->tablesize);
if (T->data[loca].key == key) {
printf("Found it\n");
//返回这个元素数据
return T->data[loca];
}
else {
int k = loca,i=1;
while (T->data[k].key != key) {
k = loca + i * i * pow(-1, i - 1);
//同样的,重复查找的操作
while (k < 0) {
i++;
k = loca + i * i * pow(-1, i - 1);
}
//找到的返回
if (T->data[k].key == key) {
printf("Found it\n");
return T->data[loca];
}
i++;
}
}
printf("Didn't find\n");
}3.伪随机探测法
公式: Hi=(Hash(key)+di) mod m ( 1
其中: m为散列表长度
di为伪随机数
这种方法了解一下就好了,随机数探测一般都不太靠谱的,所以没太必要去深入,这里就不多介绍了。
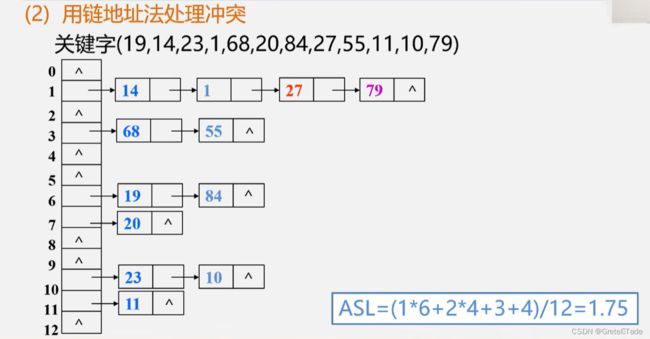
链地址法
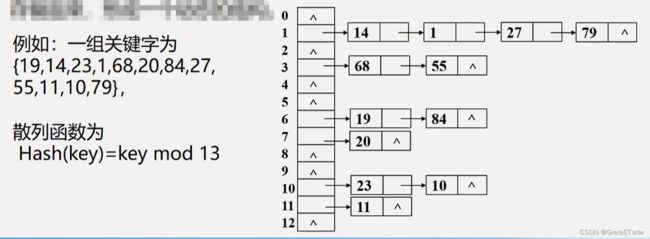
基本思想 : 相同散列地址的记录链成一单链表m个散列地址就设m个单链表,然后用一个数组将m个单链表的表头指针存储起来,形成一个动态的结构。
链地址法建立散列表步骤:
- Step1: 取数据元素的关键字key,计算其散列函数值(地址)。若该地址对应的链表为空,则将该元素插入此链表;否则执行Step2解决冲突。
- Step2: 根据选择的冲突处理方法,计算关键字key的下一个存储地址若该地址对应的链表为不为空,则利用链表的前插法或后插法将该元素插入此链表
链地址法的优点:
- 非同义词不会冲突,无“聚集”现象
- 链表上结点空间动态申请更适合于表长不确定的情况
- 更适合进行插入和删除处理
代码写法:
#include
#include
#include
#include
//数据结构
typedef struct data {
int key;
char id[10];
}Datatype;
//节点
typedef struct node {
Datatype data;
struct node* next;
}Tnode;
//头结点
typedef struct list {
int index;//头结点的下标
Tnode* link;
}Tlist;
//表结构
typedef struct table {
Tlist* list;//头结点数组
int tablesize;
}Table;
//哈希函数
int Hash(int key, int tablesize) {
return key % tablesize;
}
//创建空表
Table* create_nulltable(int m) {
Table* T = (Table*)malloc(sizeof(Table));
assert(T);
T->tablesize = m;
T->list = (Tlist*)malloc(sizeof(Tlist) * m);
assert(T->list);
return T;
}
//创建初始化表
Table* create_inittable(int m) {
Table* T = create_nulltable(m);
//对头结点数组进行初始化
for (int i = 0; i < m; i++) {
T->list[i].index = i;//下标
T->list[i].link = NULL;
}
return T;
}
//创建一个节点
Tnode* create_node(Datatype data) {
Tnode* p = (Tnode*)malloc(sizeof(Tnode));
assert(p);
p->data = data;
p->next = NULL;
return p;
}
//插入数据地址节点
void insert_index(Datatype data, Table* T) {
int loca = Hash(data.key, T->tablesize);
//尾插法
if (!T->list[loca].link)
T->list[loca].link = create_node(data);
else {
Tnode* cur = T->list[loca].link;
while (cur->next) {
cur = cur->next;
}
cur->next= create_node(data);
}
}
//查找操作
Datatype search_data(int key, Table* T) {
int loca = Hash(key, T->tablesize);
Tnode* cur = T->list[loca].link;
while (cur) {
if (cur->data.key == key) {
printf("Found it\n");
return cur->data;
}
cur = cur->next;
}
printf("No data\n");
}
//删除操作
void delete_node(int key, Table* T) {
int loca = Hash(key, T->tablesize);
Tnode* cur = T->list[loca].link;
Tnode* p=NULL;
while (cur) {
p = cur;
if (cur->data.key == key)
break;
cur = cur->next;
}
p->next = cur->next;
free(cur);
cur = NULL;
}
//打印散列表
void print(Table* T) {
assert(T);
for (int i = 0; i < T->tablesize; i++) {
printf("%d: ", T->list[i].index);
Tnode* cur = T->list[i].link;
while (cur) {
printf("%d:%s ", cur->data.key, cur->data.id);
cur = cur->next;
}
printf("\n");
}
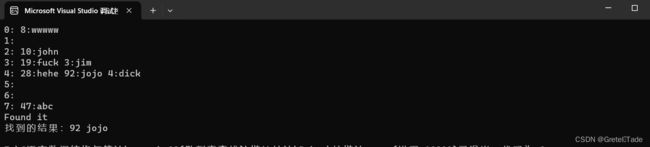
} 测试结果:
int main() {
Datatype data[] = {
{19,"fuck"},
{28,"hehe"},
{3,"jim"},
{10,"john"},
{47,"abc"},
{92,"jojo"},
{8,"wwwww"},
{4,"dick"}
};
int n = sizeof(data) / sizeof(Datatype);
Table* T = create_inittable(8);
for (int i = 0; i < n; i++) {
insert_index(data[i], T);
}
print(T);
Datatype result = search_data(92, T);
printf("找到的结果:%d %s\n", result.key, result.id);
}五.散列表的查找
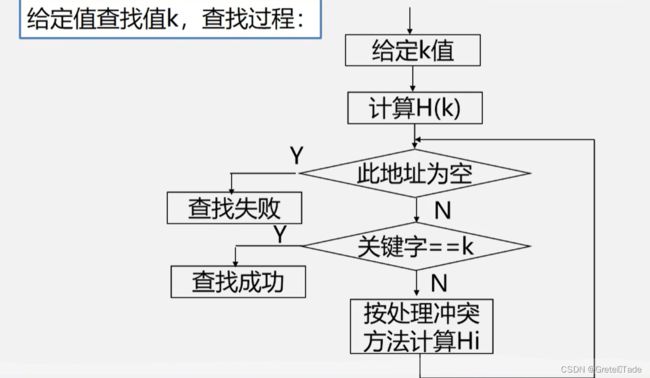
查找流程:
示例:
开放定址法:
使用平均查找长度ASL来衡量查找算法,ASL取决于
所以a 越大,表中记录数越多,说明表装得越满,发生冲突的可能性就越大,查找时比较次数就越多。ASL与装填因子a有关! 既不是严格的O(1),也不是O(n)
散列表总结:
- 散列表技术具有很好的平均性能,优于一些传统的技术
- 链地址法优于开地址法
- 除留余数法作散列函数优于其它类型函数
以上就是本期的全部内容了,我们下一期再见!
分享一张壁纸: