AcWing算法提高课----图论 笔记 （SPFA找负环）

知识点讲解

负环：在一个有向（无向）图当中， 存在一个环路，使得这个环的边权之和小于0

求负环常见方法（基于SPFA、抽屉原理）：

1. 统计每个点入队的次数，如果某个点入队n次，则说明存在负环（等价于bellman-Ford）
2. 统计当前每个点的最短路中所包含的边数，如果某点的最短路所包含的边数大于等于n，则也说明存在负环（推荐）
   
   2优于1的原因，若上图环中2的方法O(n)，1的方法O(n^2)

图中负环不一定从起点走到，可以在图中任意一个位置

若有一下图
1 2->3->4->2(负环)
方法：
将所有点入队，同时dist[i]=0，然后用第二方法判断
Q1:为什么等价于将所有点入队
A1:虚拟源点技巧。假想一个虚拟源点，虚拟源点向原图中的每个点连一条距离为0的边，若原图中存在负环，等价于新图中存在负环，新图中所有负环都可以走到。若存在负环，则证明有某些点距离虚拟源点的距离是-∞。
Q2:为什么可以讲距离初始化为0

当SPFA效率比较低的时候，可以认为存在负环（trick）
当所有点的入队次数超过2n时，我们就认为图中有很大可能是存在负环的（不一定对，若超时可以一试，某些题目有效）

例题1：AcWing904.虫洞

#include 
#include 
#include
#define ll long long
#define mem(a,b) memset(a,b,sizeof a)
#define ull unsigned long long
#define INF 0x3f3f3f3f3f3f3f3f
#define inf 0x3f3f3f3f
#define rep(i,a,b) for(auto i=a;i<=b;++i)
#define bep(i,a,b) for(auto i=a;i>=b;--i)
#define lowbit(x) x&(-x)
#define PII pair<int,int>
#define x first
#define y second
#define PLL pair<ll,ll>
#define PI acos(-1)
#define pb push_back
#define eb emplace_back
const double eps = 1e-6;
const int mod = 998244353;
const int MOD = 1e9 + 7;
const int N = 555;
const int M = 5555;
int dx[]={-1, 0, 1, 0};
int dy[]={0, 1, 0, -1};
using namespace std;

int n,m1,m2;  //m1,m2分别表示双项边、虫洞的数量
int h[N],e[M],w[M],ne[M],idx;  //邻接表
int dist[N];  //距离
int q[N],cnt[N];  //队列，每个点当前最短路径的长度,所有最短路包含的边数
bool st[N]; //判重数组

void add(int u,int v,int k){
    e[idx]=v,w[idx]=k,ne[idx]=h[u],h[u]=idx++;
}

bool SPFA(){
    int hh=0,tt=0;
    mem(dist,0);  //可以删掉 初值可以为任意值
    mem(st,0);
    mem(cnt,0);
    for(int i=1;i<=n;i++){  //所有点入队
        q[tt++]=i;
        st[i]=1;
    }
    while(hh!=tt){  //队列不空取点
        int t=q[hh++];
        if(hh==N) hh=0;  //判断是否到达终点，走到终点需要还原
        st[t]=0;  //出队标记
        for(int i=h[t];~i;i=ne[i]){ //枚举当前的临边
            int j=e[i];  //j当前点的编号
            if(dist[j]>dist[t]+w[i]){
                dist[j]=dist[t]+w[i];
                cnt[j]=cnt[t]+1;
                if(cnt[j]>=n) return 1;
                if(!st[j]){
                    q[tt++]=j;
                    if(tt==N) tt=0;
                    st[j]=1;
                } 
            }
        }
    }
    return 0;
}

inline void solve(){
    cin>>n>>m1>>m2;
    mem(h,-1);
    idx=0;
    while(m1--){
        int u,v,k;
        cin>>u>>v>>k;
        add(u,v,k);
        add(v,u,k);
    }
    while(m2--){
        int u,v,k;
        cin>>u>>v>>k;
        add(u,v,-k);
    }
    if(SPFA()) cout<<"YES"<<endl;
    else cout<<"NO"<<endl;
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) solve();
    return 0;
}

01分数规划

01分数规划是这样的一类问题，有一堆物品，每一个物品有一个收益ai，一个代价bi，我们要求一个方案使选择的∑ai/∑bi最大

找到一个环，使得环上所有的点权之和∑fi/所有边权之和∑ti，使得∑fi/∑ti
最大 --> 01分数规划

二分方法

点权放在初边上

∑(fi - mid*ti) >0 <—> 图中是否存在正环

求最短路改成求最长路
二分出一个定值->整理表达式->重新定义边权->图论算法

例题2：AcWing361.观光奶牛

答案：

#include 
#include 
#include
#define ll long long
#define mem(a,b) memset(a,b,sizeof a)
#define ull unsigned long long
#define INF 0x3f3f3f3f3f3f3f3f
#define inf 0x3f3f3f3f
#define rep(i,a,b) for(auto i=a;i<=b;++i)
#define bep(i,a,b) for(auto i=a;i>=b;--i)
#define lowbit(x) x&(-x)
#define PII pair<int,int>
#define x first
#define y second
#define PLL pair<ll,ll>
#define PI acos(-1)
#define pb push_back
#define eb emplace_back
const double eps = 1e-6;
const int mod = 998244353;
const int MOD = 1e9 + 7;
const int N = 1111;
const int M = 5555;
int dx[]={-1, 0, 1, 0};
int dy[]={0, 1, 0, -1};
using namespace std;

int n,m;
int wf[N];
int h[N],e[M],wt[M],ne[M],idx;  //邻接表
double dist[N];  //距离
int q[N],cnt[N];  //队列，每个点当前最短路径的长度,所有最短路包含的边数
bool st[N]; //判重数组

void add(int u,int v,int w){
    e[idx]=v,wt[idx]=w,ne[idx]=h[u],h[u]=idx++;
}

bool judge(double mid){
    int hh=0,tt=0;
    //mem(dist,0);
    mem(st,0);
    mem(cnt,0);
    for(int i=1;i<=n;i++){  //所有点入队
        q[tt++]=i;
        st[i]=1;
    }
    while(hh!=tt){  //队列不空取点
        int t=q[hh++];
        if(hh==N) hh=0;  //判断是否到达终点，走到终点需要还原
        st[t]=0;  //出队标记
        for(int i=h[t];~i;i=ne[i]){ //枚举当前的临边
            int j=e[i];  //j当前点的编号
            if(dist[j]<dist[t]+wf[t]-mid*wt[i]){
                dist[j]=dist[t]+wf[t]-mid*wt[i];
                cnt[j]=cnt[t]+1;
                if(cnt[j]>=n) return 1;
                if(!st[j]){
                    q[tt++]=j;
                    if(tt==N) tt=0;
                    st[j]=1;
                } 
            }
        }
    }
    return 0;
}

inline void solve(){
    cin>>n>>m;
    mem(h,-1);
    idx=0;
    rep(i,1,n) cin>>wf[i];
    while(m--){
        int u,v,w;
        cin>>u>>v>>w;
        add(u,v,w);
        //add(v,u,k);
    }
    double l=0,r=1000;
    while(r-l>1e-4){
        double mid=(l+r)/2;
        if(judge(mid)) l=mid;
        else r=mid;
    }
    cout<<fixed<<setprecision(2)<<r<<endl;
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    //cin>>t;
    while(t--) solve();
    return 0;
}

例题3：AcWing1165.单词环

• Q:
  • a.建图
  • b.01分数规划
  • c.数据量大、优化

建图方式：
把字符串看成边 e.g. ababc -》 ab->ba(5)

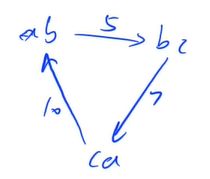
答案：

#include 
#include 
#include
#define ll long long
#define mem(a,b) memset(a,b,sizeof a)
#define ull unsigned long long
#define INF 0x3f3f3f3f3f3f3f3f
#define inf 0x3f3f3f3f
#define rep(i,a,b) for(auto i=a;i<=b;++i)
#define bep(i,a,b) for(auto i=a;i>=b;--i)
#define lowbit(x) x&(-x)
#define PII pair<int,int>
#define x first
#define y second
#define PLL pair<ll,ll>
#define PI acos(-1)
#define pb push_back
#define eb emplace_back
const double eps = 1e-6;
const int mod = 998244353;
const int MOD = 1e9 + 7;
const int N = 700;
const int M = 1e5 + 10;
int dx[]={-1, 0, 1, 0};
int dy[]={0, 1, 0, -1};
using namespace std;

int n,m;
int wf[N];
int h[N],e[M],wt[M],ne[M],idx;  //邻接表
double dist[N];  //距离
int q[N],cnt[N];  //队列，每个点当前最短路径的长度,所有最短路包含的边数
bool st[N]; //判重数组

void add(int u,int v,int w){
    e[idx]=v,wt[idx]=w,ne[idx]=h[u],h[u]=idx++;
}

bool judge(double mid){
    int hh=0,tt=0;
    //mem(dist,0);
    mem(st,0);
    mem(cnt,0);
    for(int i=0;i<676;i++){  //所有点入队
        q[tt++]=i;
        st[i]=1;
    }
    int tot=0;
    while(hh!=tt){  //队列不空取点
        int t=q[hh++];
        if(hh==N) hh=0;  //判断是否到达终点，走到终点需要还原
        st[t]=0;  //出队标记
        for(int i=h[t];~i;i=ne[i]){ //枚举当前的临边
            int j=e[i];  //j当前点的编号
            if(dist[j]<dist[t]+wt[i]-mid){
                dist[j]=dist[t]+wt[i]-mid;
                cnt[j]=cnt[t]+1;
                if(++tot>2*n) return 1;
                if(cnt[j]>=N) return 1;
                if(!st[j]){
                    q[tt++]=j;
                    if(tt==N) tt=0;
                    st[j]=1;
                } 
            }
        }
    }
    return 0;
}

inline void solve(){
    char s[1111];
    while(cin>>n&&n){
        mem(h,-1);
        rep(i,1,n){
            cin>>s;
            //cout<
            int len=strlen(s);
            if(len>=2){
                int l=(s[0]-'a')*26+s[1]-'a';
                int r=(s[len-2]-'a')*26+s[len-1]-'a';
                add(l,r,len);
            }
        }
        if(!judge(0)) cout<<"No solution"<<endl;
        else{
            double l=0,r=1000;
            while(r-l>1e-4){
                double mid=(l+r)/2;
                if(judge(mid)) l=mid;
                else r=mid;
            }
            cout<<r<<endl;
        }
    }
    //cout<
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    //cin>>t;
    while(t--) solve();
    return 0;
}

经验上的trick可以换成另一种方式 把spfa中的栈换成队列,一定对蛋效率不稳,不过有负环时效果很好
上述judge变换