数据结构与算法（图论系列）------拓扑排序详解

定义

在图论中，拓扑排序（Topological Sorting）是一个有向无环图（DAG, Directed Acyclic Graph）的所有顶点的线性序列。且该序列必须满足下面两个条件：

1. 每个顶点出现且只出现一次。
2. 若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。

有向无环图（DAG）才有拓扑排序，非DAG图没有拓扑排序一说。

例如，下面这个图：

为什么会有拓扑排序？拓扑排序有何作用？

举个例子，学习java系列的教程

就比如学习java系类(部分)从java基础，到jsp/servlet，到ssm，到springboot，springcloud等是个循序渐进且有依赖的过程。在jsp学习要首先掌握java基础和html基础。学习框架要掌握jsp/servlet和jdbc之类才行。那么，这个学习过程即构成一个拓扑序列。当然这个序列也不唯一，你可以对不关联的学科随意选择顺序(比如html和java可以随便先开始哪一个。)

那上述序列可以简单表示为：

其中五种均为可以选择的学习方案，对课程安排可以有参考作用，当然，五个都是拓扑序列。只是选择的策略不同！

• 一些其他注意：

1. DGA：有向无环图
2. AOV网：数据在顶点 可以理解为面向对象
3. AOE网：数据在边上，可以理解为面向过程！

而我们通俗一点的说法，就是按照某种规则将这个图的顶点取出来，这些顶点能够表示什么或者有什么联系。

• 规则：

1. 图中每个顶点只出现一次。
2. A在B前面，则不存在B在A前面的路径。(不能成环！！！！)
3. 顶点的顺序是保证所有指向它的下个节点在被指节点前面！(例如A—>B—>C那么A一定在B前面，B一定在C前面)。所以，这个核心规则下只要满足即可，所以拓扑排序序列不一定唯一！

简单实现

    queue<int>q;
    vector<int>edge[n];
    for(int i=0;i<n;i++)  //n  节点的总数
        if(in[i]==0) q.push(i);  //将入度为0的点入队列
    vector<int>ans;   //ans 为拓扑序列
    while(!q.empty())
    {
        int p=q.front(); q.pop(); // 选一个入度为0的点，出队列
        ans.push_back(p);
        for(int i=0;i<edge[p].size();i++)
        {
            int y=edge[p][i];
            in[y]--;
            if(in[y]==0)
                q.push(y);  
        }
    }
    if(ans.size()==n)   
    {
        for(int i=0;i<ans.size();i++)
            printf( "%d ",ans[i] );
        printf("\n");
    }
    else printf("No Answer!\n");   //  ans 中的长度与n不相等，就说明无拓扑序列

算法分析及具体代码实现

对于拓扑排序，如何用代码实现呢？对于拓扑排序，虽然在上面介绍了思路和流程，很通俗易懂。但是实际上代码的实现还是很需要斟酌的，如何在空间和时间上能够得到较好的平衡且取得较好的效率？

首先要考虑存储。对于节点，首先他有联通点这么多属性。遇到稀疏矩阵还是用邻接表比较好。因为一个节点的指向节点较少，用邻接矩阵较浪费资源。具体关于邻接矩阵和邻接表的学习参见此博客

另外，如果是1，2，3，4，5，6这样的序列求拓扑排序，我们可以考虑用数组，但是如果遇到1，2，88，9999类似数据，可以考虑用map中转一下。

那么，我们具体的代码思想为：

1. 新建node类，包含节点数值和它的指向(这里直接用list集合替代链表了)
2. 一个数组包含node(这里默认编号较集中)。初始化，添加每个节点指向的时候同时被指的节点入度+1！(A—>C)那么C的入度+1；
3. 扫描一遍所有node。将所有入度为0的点加入一个栈(队列)。
4. 当栈(队列)不空的时候，抛出其中任意一个node(栈就是尾，队就是头，顺序无所谓，上面分析了只要同时入度为零可以随便选择顺序)。将node输出，并且node指向的所有元素入度减一。如果某个点的入度被减为0，那么就将它加入栈(队列)。
5. 重复上述操作，直到栈为空。

这里主要是利用栈或者队列储存入度只为0的节点，只需要初次扫描表将入度为0的放入栈(队列)中。
这里你或许会问为什么。

因为节点之间是有相关性的，一个节点若想入度为零，那么它的父节点(指向节点)肯定在它为0前入度为0，拆除关联箭头。从父节点角度，它的这次拆除联系，可能导致被指向的入读为0，也可能不为0(还有其他节点指向儿子)。

#include
#include 
#include 
using namespace std;

/************************类声明************************/
class Graph
{
    int V;             // 顶点个数
    list<int> *adj;    // 邻接表
    queue<int> q;      // 维护一个入度为0的顶点的集合
    int* indegree;     // 记录每个顶点的入度
public:
    Graph(int V);                   // 构造函数
    ~Graph();                       // 析构函数
    void addEdge(int v, int w);     // 添加边
    bool topological_sort();        // 拓扑排序
};

/************************类定义************************/
Graph::Graph(int V)
{
    this->V = V;
    adj = new list<int>[V];

    indegree = new int[V];  // 入度全部初始化为0
    for(int i=0; i<V; ++i)
        indegree[i] = 0;
}

Graph::~Graph()
{
    delete [] adj;
    delete [] indegree;
}

void Graph::addEdge(int v, int w)
{
    adj[v].push_back(w); 
    ++indegree[w];
}

bool Graph::topological_sort()
{
    for(int i=0; i<V; ++i)
        if(indegree[i] == 0)
            q.push(i);         // 将所有入度为0的顶点入队

    int count = 0;             // 计数，记录当前已经输出的顶点数 
    while(!q.empty())
    {
        int v = q.front();      // 从队列中取出一个顶点
        q.pop();

        cout << v << " ";      // 输出该顶点
        ++count;
        // 将所有v指向的顶点的入度减1，并将入度减为0的顶点入栈
        list<int>::iterator beg = adj[v].begin();
        for( ; beg!=adj[v].end(); ++beg)
            if(!(--indegree[*beg]))
                q.push(*beg);   // 若入度为0，则入栈
    }

    if(count < V)
        return false;           // 没有输出全部顶点，有向图中有回路
    else
        return true;            // 拓扑排序成功
}

测试如下DAG图：

int main()
{
    Graph g(6);   // 创建图
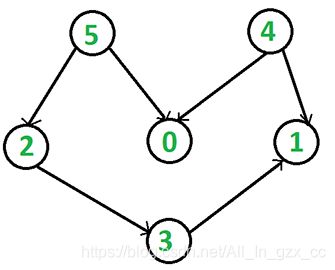
    g.addEdge(5, 2);
    g.addEdge(5, 0);
    g.addEdge(4, 0);
    g.addEdge(4, 1);
    g.addEdge(2, 3);
    g.addEdge(3, 1);

    g.topological_sort();
    return 0;
}

输出结果是 4, 5, 2, 0, 3, 1。这是该图的拓扑排序序列之一。

每次在入度为0的集合中取顶点，并没有特殊的取出规则，随机取出也行，这里使用的queue。取顶点的顺序不同会得到不同的拓扑排序序列，当然前提是该图存在多个拓扑排序序列。

由于输出每个顶点的同时还要删除以它为起点的边，故上述拓扑排序的时间复杂度为O(V+E)。