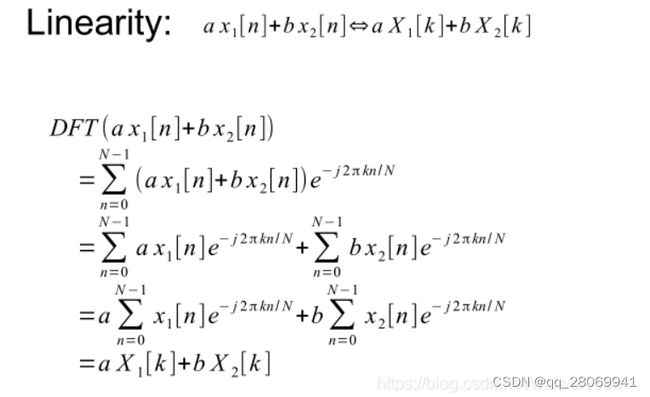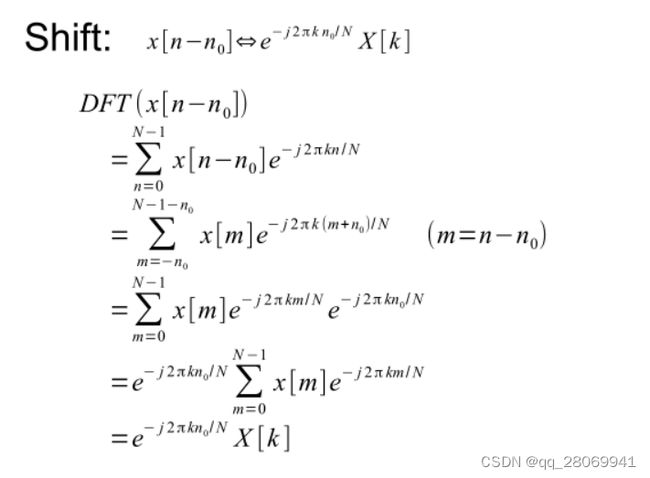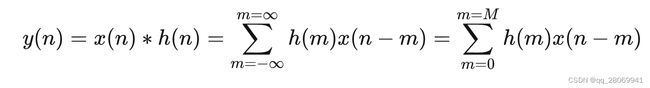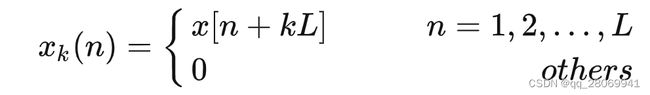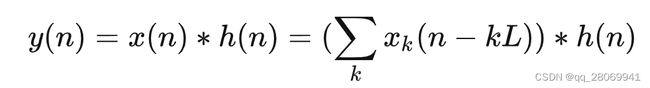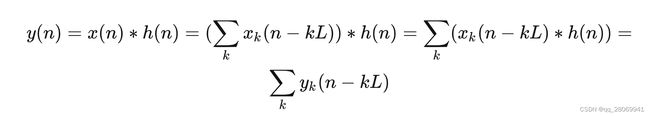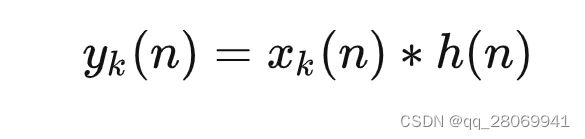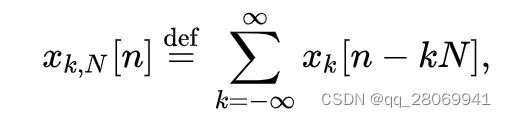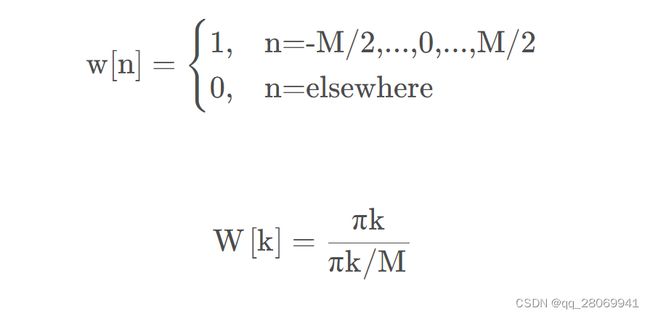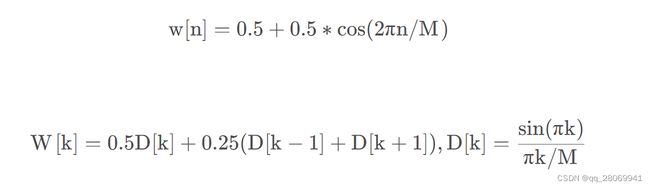用Python做信号处理
用Python做信号处理
声明:本文中设计的知识和代码大部分来自:芥末的无奈的博客_CSDN博客-音频处理,c++,keras领域博主 以及 凌逆战 - 博客园 (cnblogs.com) 两位大神所写,非常感谢开源精神。我自己总结并自己手打一遍代码进行学习,用作自己之后的回顾和复习,绝不参与任何商业活动,如有侵权,请联系我进行删除,非常感谢。
文章目录
- 用Python做信号处理
-
- 1、Python 生成正弦信号
- 2、Python读取与保存音频信号
- 3、离散傅里叶变换(DFT)
-
- 1、Scipy 包的FFT
- 2、通过矩阵运算求DFT
- 3、傅里叶变换的基本性质
-
- 一、线性性质
- 二、平移性质
- 三、对称性质
- 四、卷积性质
- 4、卷积 (Convolution)
-
- FFT卷积(快速傅里叶变换)
-
- 在干净语音信号中增加混响 (傅里叶变换的应用)
- 用FFT将信号转换到频域去除能量较低的底噪 (傅里叶变换的应用)
- 更快的卷积方法(overlap-add和overlap-save)
-
- Overlap-add
- Overlap-save
- 5、短时傅里叶变换 STFT
-
- 短时傅里叶变换是什么?我们为什么要用它?
- 窗函数
-
- 矩形窗:
- Hanning窗(升余弦窗)
- Hamming: 改进升余弦窗
- Blackman窗(二阶升余弦窗)
- STFT的原理及实现:
- Mel频谱以及Mel倒谱系数(MFCC)
-
- 1、预处理
-
- ① 预加重
- ②、分帧
- ③、加窗 (window)
- 2、FFT
- 3、功率谱
- 4、Mel 刻度滤波器组
- 5、Mel 频率倒谱系数(MFCC)
- 使用方法
- 6、语音数据增强
-
- 一、导入原始语音数据
- 二、增加噪声 (Noise addition) (时域)
-
- ①、控制噪声因子
- ②、控制信噪比
- 三、混响增强 (Reverberation addition) (时域)
-
- 方法一:Pyroomacoustic 库实现音频加混响
- 方法二:Image Source Method 算法
- 四、波形位移 (time shifting) (时域)
- 五、音高(音调)增强 (Pitch shifting) (频域)
1、Python 生成正弦信号
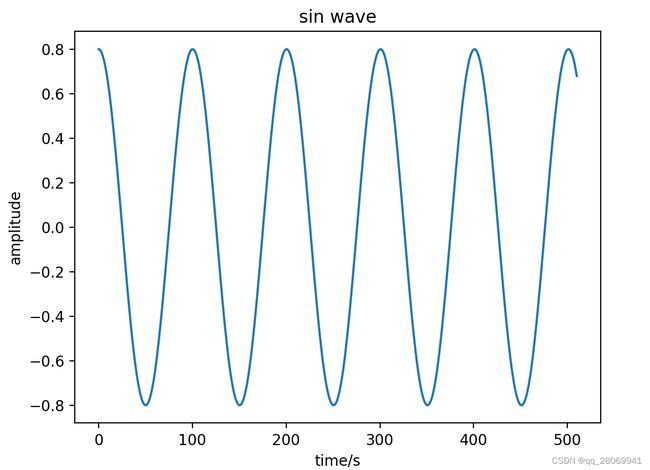
假设我们想用python生成一个正弦信号 x [ n ] = A c o s ( 2 π f n T + Φ ) x[n] = Acos(2\pi fnT+\Phi) x[n]=Acos(2πfnT+Φ) ,其中 A A A为幅度, f f f为信号频率, n n n为时间下标, T = 1 / f s T=1/f_s T=1/fs为采样间隔, f s f_s fs 为采样频率, Φ \Phi Φ 为相位
### 这个程序用来生成正弦信号
import numpy as np
import matplotlib.pyplot as plt
def generate_sinusoid(N,A,f0,fs,phi):
'''
:param N(int): number of samples
:param A(float): amplitude
:param f0(float): frequency
:param fs(float): sample rate
:param phi(float): initial phase
:return: x(numpy array): sinusoid signal which length is M
'''
T = 1/fs
n = np.arange(N)
x = A * np.cos(2*f0*np.pi*n*T+phi)
return x
def generate_sinusoid_2(t,A,f0,fs,phi):
'''
:param t(float): the time of generated signal
:param A(float): amplitude
:param f0(float): frequency
:param fs(float): sample rate
:param phi(float): initial phase
:return: x(numpy array): sinusoid signal which length is M
'''
T = 1.0/fs
N = t/T
return generate_sinusoid(N,A,f0,fs,phi)
if __name__ == "__main__":
N = 511
A = 0.8
f0 = 440
fs = 44100
t = 0.02
n = np.arange(0,0.02,1/fs)
phi = 0
x = generate_sinusoid(N,A,f0,fs,phi)
x2 = generate_sinusoid_2(t,A,f0,fs,phi)
plt.figure()
plt.plot(x)
plt.xlabel('Number')
plt.ylabel('amplitude')
plt.title('sin wave')
plt.figure()
plt.plot(n,x2)
plt.xlabel('time/s')
plt.ylabel('amplitude')
plt.title('sin wave')
plt.show()
运行结果如下:
2、Python读取与保存音频信号
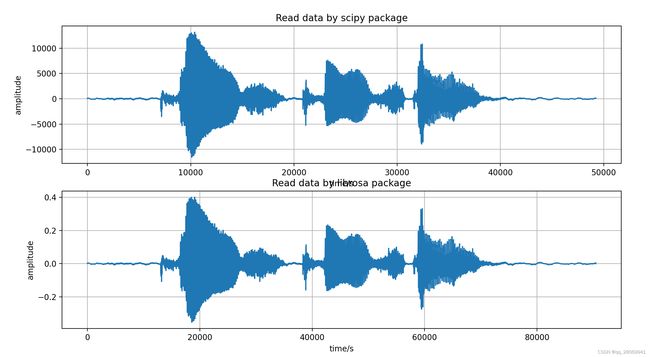
Python有很多种方法和库读取音频信号,其中推荐和常用的主要是scipy库和librosa库
# This scipt is used scipy library to read the sound file data
from scipy.io import wavfile
import matplotlib.pyplot as plt
import librosa
fs,sig = wavfile.read('data/[email protected]')
print("sampling rate = ") # 24000
print(fs)
f1 = plt.figure(1)
plt.subplot(211)
plt.plot(sig)
plt.grid()
plt.title('Read data by scipy package')
plt.xlabel('time/s')
plt.ylabel('amplitude')
signal,sample_rate = librosa.load('data/[email protected]',sr = 44100)
print("sampling_rate = " ) # 44100, In librosa package, we can input the sampling rate by ourselves
print(sample_rate)
plt.subplot(212)
plt.plot(signal)
plt.grid()
plt.title('Read data by librosa package')
plt.xlabel('time/s')
plt.ylabel('amplitude')
plt.show()
# store
path = 'output.wav'
librosa.output.write_wav(path,data.astype(np.float32),sr = sample_rate)
3、离散傅里叶变换(DFT)
离散傅里叶变换,可以将采样及量化后的离散信号变换到频域:
在这里,我不详细阐述DFT的理论及背后的物理意义,我更关心怎么用python实现DFT
1、Scipy 包的FFT
这里我们可以使用Scipy库中的FFT算法计算DFT(这里需要输入信号长度为 2 n 2^n 2n 才可以使用FFT,若不为 2 n 2^n 2n,那么默认为DFT)
### 这个程序用来生成正弦信号
import numpy as np
import matplotlib.pyplot as plt
def generate_sinusoid(N,A,f0,fs,phi):
'''
:param N(int): number of samples
:param A(float): amplitude
:param f0(float): frequency
:param fs(float): sample rate
:param phi(float): initial phase
:return: x(numpy array): sinusoid signal which length is M
'''
T = 1/fs
n = np.arange(N)
x = A * np.cos(2*f0*np.pi*n*T+phi)
return x
def generate_sinusoid_2(t,A,f0,fs,phi):
'''
:param t(float): the time of generated signal
:param A(float): amplitude
:param f0(float): frequency
:param fs(float): sample rate
:param phi(float): initial phase
:return: x(numpy array): sinusoid signal which length is M
'''
T = 1.0/fs
N = t/T
return generate_sinusoid(N,A,f0,fs,phi)
def test01():
N = 511
A = 0.8
f0 = 440
fs = 44100
t = 0.02
n = np.arange(0, 0.02, 1 / fs)
phi = 0
x = generate_sinusoid(N, A, f0, fs, phi)
x2 = generate_sinusoid_2(t, A, f0, fs, phi)
plt.figure()
plt.plot(x)
plt.xlabel('Number')
plt.ylabel('amplitude')
plt.title('sin wave')
plt.figure()
plt.plot(n, x2)
plt.xlabel('time/s')
plt.ylabel('amplitude')
plt.title('sin wave')
plt.show()
def test02():
from scipy.fftpack import fft
N = 511
A = 0.8
f0 = 440
fs = 44100
phi = 1.0
x = generate_sinusoid(N,A,f0,fs,phi)
# do fft
X = fft(x)
mX = np.abs(X) # magnitude
pX = np.angle(X) # phase
# plot the magnitude and phase
plt.subplot(2,1,1)
plt.plot(mX)
plt.subplot(2,1,2)
plt.plot(pX)
plt.show()
if __name__ == "__main__":
test02()
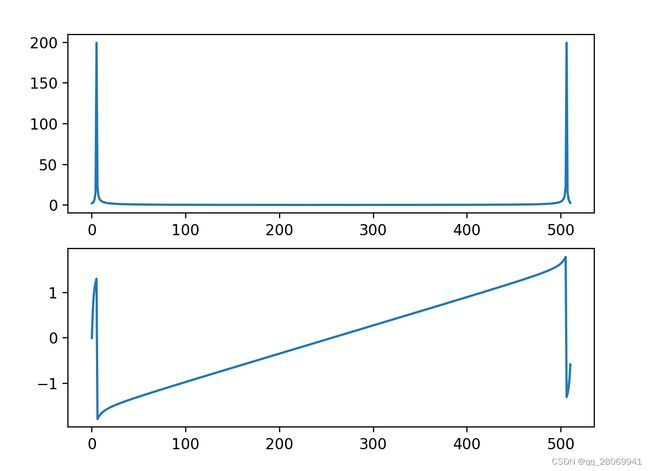
2、通过矩阵运算求DFT
通过DFT的定义式,我们可以考虑将其用矩阵相乘的方式写出来,也就是会变为:
其中 S k = e − j 2 π k n / N S_k = e^{-j2\pi kn/N} Sk=e−j2πkn/N ,那么我们可以考虑构建出S矩阵
def generate_complex_sinusoid_matrix(N):
'''
:param N(int): length of complex sinusoid in samples
:return: S_k(numpy_array): matrix
'''
n = np.arange(N)
n = np.expand_dims(n,axis = 1) # 扩展维度,将一维矩阵转换为二维矩阵,方便后面的矩阵相乘
k = n
m = n.T * k / N
S = np.exp(1j*2*np.pi*m)
return np.conjugate(S)
def test03():
N = 511
A = 0.8
f0 = 440
fs = 44100
phi = 1.0
x = generate_sinusoid(N,A,f0,fs,phi)
# do fft
S = generate_complex_sinusoid_matrix(N)
X_2 = np.dot(S,x)
mX = np.abs(X_2)
pX = np.angle(X_2)
plt.subplot(2,1,1)
plt.plot(mX)
plt.subplot(2,1,2)
plt.plot(pX)
plt.show()
3、傅里叶变换的基本性质
傅里叶变换主要有:1、线性性质 2、平移性质 3、对称性质 4、卷积性质 四种性质。
一、线性性质
两个函数之和的傅里叶变换等于各自变换之和
# 这个程序用来证明傅里叶变换的四种性质
import numpy as np
from scipy.fftpack import fft
import matplotlib.pyplot as plt
def generate_complex_signal(num_sample,k0):
'''
:param num_sample: N
:param k0: the frequency
:return: sin wave
'''
n = np.arange(num_sample)
x = np.exp(1j*2*np.pi*k0*n/num_sample)
return x
def Linearity():
num_sample = 100
k0 = 20
x1 = generate_complex_signal(num_sample, k0)
num_sample = 100
k0 = 10
x2 = generate_complex_signal(num_sample, k0)
X1 = fft(x1)
X2 = fft(x2)
mX1 = np.abs(X1)
mX2 = np.abs(X2)
x12 = x1 + x2
X12 = fft(x12)
mX12 = np.abs(X12)
plt.figure()
plt.subplot(321)
plt.plot(x1)
plt.subplot(322)
plt.plot(x2)
plt.subplot(323)
plt.plot(mX1)
plt.subplot(324)
plt.plot(mX2)
plt.subplot(325)
plt.plot(mX1 + mX2)
plt.subplot(326)
plt.plot(mX12)
plt.show();
if __name__ == "__main__":
Linearity()
![]()
二、平移性质
在时域上对信号进行平移,等价于在频域的复平面上旋转一个角度,相反的,频域的复平面上旋转一个角度,等价于时域上的平移,并且平移只对DFT的相位有影响,但是不会改变DFT的幅度。
def shift():
x1 = np.linspace(0, 1.0, 50)
x1 = np.append(x1, 0)
x1 = np.append(x1, np.linspace(-1.0, 0, 50))
shifted_x = np.roll(x1, 10) # shift signal
X1 = fft(x1)
shiftedX = fft(shifted_x)
mX1 = np.abs(X1)
pX1 = np.angle(X1)
pX1 = np.unwrap(pX1)
mshiftedX = np.abs(shiftedX)
pshiftedX = np.angle(shiftedX)
pshiftedX = np.unwrap(pshiftedX)
# plot the results
plt.subplot(321)
plt.plot(x1)
plt.subplot(322)
plt.plot(shifted_x)
plt.subplot(323)
plt.plot(mX1)
plt.subplot(324)
plt.plot(mshiftedX)
plt.subplot(325)
plt.plot(pX1)
plt.subplot(326)
plt.plot(pshiftedX)
plt.show();
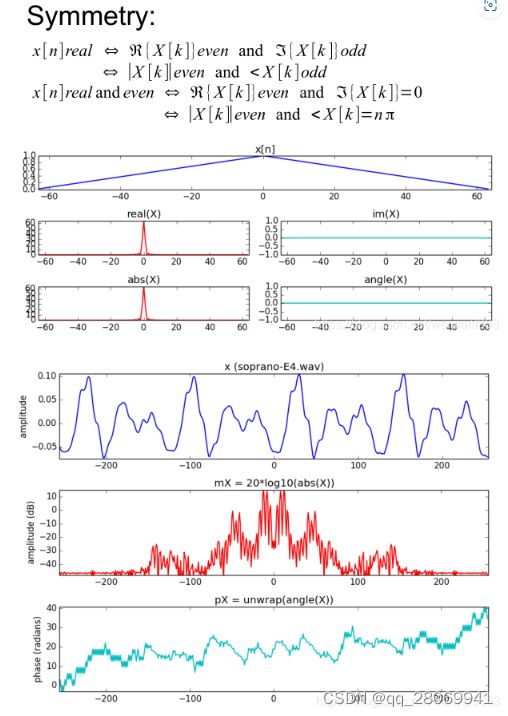
三、对称性质
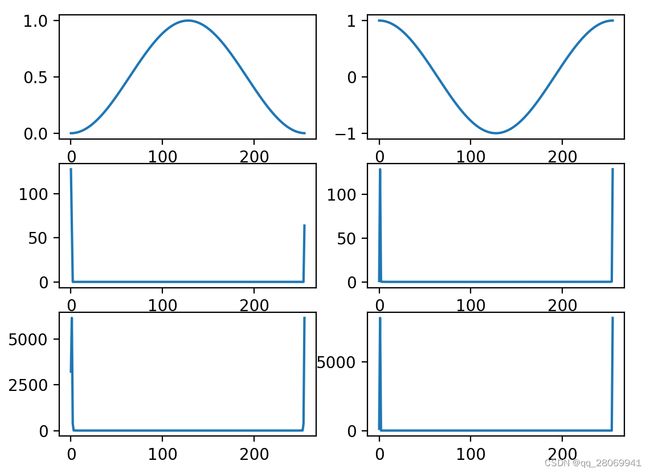
四、卷积性质
def convolution():
from scipy.signal import get_window
x1 = get_window('hanning',256)
x2 = np.cos(np.linspace(0,2*np.pi,256))
conv_x = np.convolve(x1,x2,'same')
X1 = fft(x1)
X2 = fft(x2)
CX = fft(conv_x)
plt.subplot(321)
plt.plot(x1)
plt.subplot(322)
plt.plot(x2)
plt.subplot(323)
plt.plot(np.abs(X1))
plt.subplot(324)
plt.plot(np.abs(X2))
plt.subplot(325)
plt.plot(np.abs(CX))
plt.subplot(326)
plt.plot(np.abs(X1 * X2))
plt.show()
4、卷积 (Convolution)
在之前的DFT的介绍当中,我们提及到了卷积性质,先来复习一下卷积的定义如下:
x [ h ] ∗ h [ n ] = ∑ k = − ∞ ∞ x [ k ] h [ n − k ] = y [ n ] , n ∈ Z x[h]*h[n] = \sum_{k=-\infty}^{\infty}x[k]h[n-k] = y[n], n\in {Z} x[h]∗h[n]=k=−∞∑∞x[k]h[n−k]=y[n],n∈Z
也就是说我们输入信号 x [ n ] x[n] x[n] 经过一个冲激响应为 h [ n ] h[n] h[n] 的LTI系统后,得到的输出为 y [ n ] y[n] y[n],这个过程就是卷积,那么我们如何获取系统的 h [ n ] h[n] h[n]呢,我们只需要对这个系统输入一个理想的单位冲激信号 δ ( t ) \delta(t) δ(t) 就可以了,但是在现实世界中,不存在理想的 δ ( t ) \delta(t) δ(t),所以我们考虑用另外的方法,关于房间脉冲响应的测量的原理请看这:Impulse Response Measurement 脉冲响应测量 - 知乎 (zhihu.com)
那么同样的我们想要对输入声源加入一个混响也就可以通过卷积实现,我们可以将一个封闭房间的脉冲响应与我们的输入信号相卷积,得到的输出就是加入了这个房间声学性能后的混响音频。假设录制得到的房间脉冲响应为 h ( n ) h(n) h(n),长度为 n n n,输入信号 x ( n ) x(n) x(n),长度为 m m m.
但是从卷积定义开始,有个问题在于其计算复杂度比较高,首先要对脉冲响应信号翻折然后平移,之后要对每个采样点进行N次乘法以及N次加法,所以总共有乘法 N ∗ M N*M N∗M 次以及加法 N ∗ M N*M N∗M次,那么算法复杂度就是 O ( N ∗ M ) O(N*M) O(N∗M)。
所以为了提高计算性能,研究人员提出了一些快速卷积的方法(如FFT,overlap-save,overlap-add)等,在之后会逐步介绍。
FFT卷积(快速傅里叶变换)
在之前我们提到过的卷积定理,在时域上做卷积就是在频域上做乘积,所以利用这个定理,我们就可以将 h ( n ) h(n) h(n) 和 x ( n ) x(n) x(n)通过快速傅里叶变换(FFT)得到其在频域表达式 H ( w ) H(w) H(w)和 X ( w ) X(w) X(w),最后让他们两相乘,得到 Y ( w ) Y(w) Y(w),最后将 Y ( w ) Y(w) Y(w)通过IFFT从频域变回时域即可。关于 F F T FFT FFT的原理,我们一般关心Radix-2算法,也就是要求输入信号长度必须是 2 n 2^n 2n ,并根据指数项的周期性可以得到FFT的蝶式单元,详情可以看这篇文章:[精品讲义]—快速傅里叶变换(Fast Fourier Transformation) - 知乎 (zhihu.com) 以及英文版的推导:FFT ~ 快速傅里叶变换 (aalto.fi),这种采用分而治之思想处理的算法会让计算复杂度在 O ( n l o g ( n ) ) O(nlog(n)) O(nlog(n))
## This script is used to implement the radix-2 FFT algorithm
import numpy as np
import matplotlib.pyplot as plt
def naiveFFT(x):
N = x.size
X = np.ones(N)*(0+0j)
for k in range(N):
A = np.ones(N)*(0+0j)
for n in range(N):
A[n] = x[n] * np.exp(-np.complex(0,2*np.pi*k*n/N))
X[k] = sum(A)
return X
def FFT(x):
'''
:param x: The input signal in time domain
:return: X: The output signal in frequency domain
'''
x = np.array(x,dtype=float)
N = int(x.size)
# Use the naive version when the size is small enough
if N <= 8:
return naiveFFT(x)
else:
# Calculate the first half of the W vector
k = np.arange(N/2)
W = np.exp(-2j*np.pi*k/N)
evens = FFT(x[::2])
odds = FFT(x[1::2])
return np.concatenate([evens + (W * odds), evens- (W*odds)]) # concate the two sides
return 0
def generate_sinusoid(N,A,f0,fs,phi):
'''
:param N(int): number of samples
:param A(float): amplitude
:param f0(float): frequency
:param fs(float): sample rate
:param phi(float): initial phase
:return: x(numpy array): sinusoid signal which length is M
'''
T = 1/fs
n = np.arange(N)
x = A * np.cos(2*f0*np.pi*n*T+phi)
return x
def test01():
N = 2 ** 10
A = 0.8
f0 = 440
fs = 44100
phi = 0
t = np.linspace(0,10,N)
T = t[1] - t[0]
signal = generate_sinusoid(N,A,f0,fs,phi)
fft = FFT(signal)
# Calculate the frequency scale for the plot
freq_scale = np.linspace(0,1/T,N)
print("sampling_frequency:" + str(1/T))
# plot the results
plt.figure()
plt.subplot(311)
plt.plot(t,signal)
plt.title("time domain")
plt.subplot(312)
plt.plot(freq_scale,np.absolute(fft))
plt.title('Frequency domain by own')
plt.subplot(313)
plt.plot(freq_scale,np.absolute(np.fft.fft(signal)))
plt.title("Frequency domain by scipy")
plt.show()
if __name__ == '__main__':
test01()
而我们在这个从时域转换到频域再相乘的过程中,会有一些问题,一个是 h ( n ) h(n) h(n) 和 x ( n ) x(n) x(n) 的长度通常不相同,但是在频域相乘过程中,我们需要 H ( w ) H(w) H(w) 和 X ( w ) X(w) X(w) 的长度是相同的,所以我们通过在信号尾部进行 z e r o − p a d d i n g zero-padding zero−padding 操作,将 h ( n ) h(n) h(n) 和 x ( n ) x(n) x(n) 填充到相同长度 k k k, ( k ≥ M + N − 1 ) (k\geq M+N-1) (k≥M+N−1)。我们在这里用一些案例来演示。
总而言之,运用FFT算法对两个长度不同信号进行卷积的步骤如下:
- 计算K的大小,确保 K ≥ M + N − 1 K\geq M+N-1 K≥M+N−1,然后最好能够保证其为2的次方长度,这样能够满足FFT的使用条件
- 利用zero-padding将 x ( n ) x(n) x(n) 和 h ( n ) h(n) h(n) 均填充到k的长度,然后利用卷积定理,将其两分别变换到频域再相乘 Y = X ∗ H Y=X*H Y=X∗H
- 最后将输出信号利用IFFT变换回时域,就可以得到最终的卷积效果,也就是最终的输入信号经过LTI系统后的结果。
在干净语音信号中增加混响 (傅里叶变换的应用)
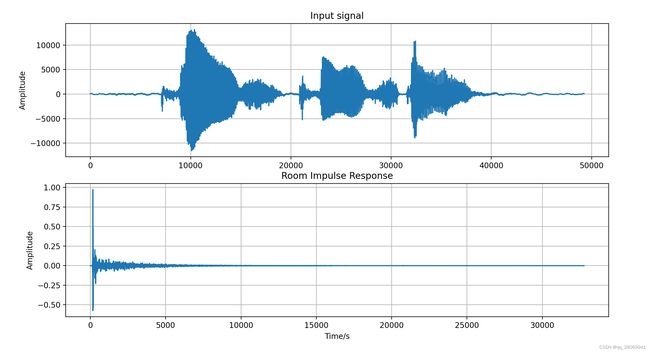
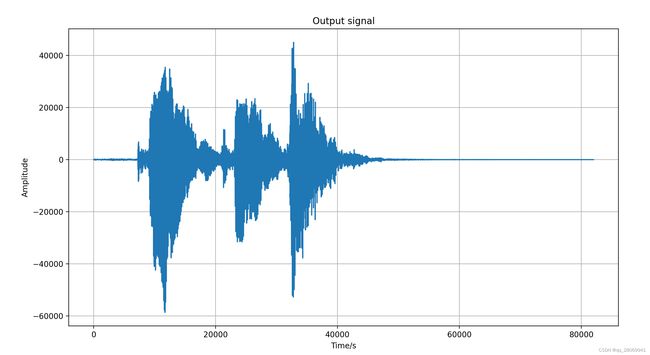
这里我们采用一个采样频率为24kHz的语音信号"Please Call Stella"作为输入信号 x ( n ) x(n) x(n), 并采用一个采样频率为16kHz的Lecture房间的RIR,并用Librosa读取时候用24kHz采样率读取。其在时域的波形如下:
可以很明显的看到 x ( n ) x(n) x(n) 和 h ( n ) h(n) h(n) 的长度不相同,其中 x ( n ) x(n) x(n) 长度为49237,而 h ( n ) h(n) h(n) 长度为32768,所以我们考虑将他们zero-padding至相同的长度,长度最好为 K ≥ N + M − 1 K \geq N+M-1 K≥N+M−1 且为2的倍数(方便之前所提及的Radix-2 FFT算法。
代码如下:
# This script is used to convolve the different input signal and impulse response
import numpy as np
import matplotlib.pyplot as plt
from scipy.io import wavfile
import librosa
def pad_zeros_to(x,new_length):
output = np.zeros((new_length,))
output[:x.shape[0]] = x
return output
def next_power_of_2(n):
return 1 << (int(np.log2(n-1))+1)
def fft_convolution(x,h,K=None):
Nx = x.shape[0]
Nh = h.shape[0]
Ny = Nx + Nh - 1
if K is None:
K = next_power_of_2(Ny)
X = np.fft.fft(pad_zeros_to(x,K))
H = np.fft.fft(pad_zeros_to(h,K))
Y = X*H
y = np.real(np.fft.ifft(Y))
return y[:Ny]
def data_read():
# Read the input clear signal
fs, signal = wavfile.read('data/[email protected]')
# Read the RIR
ir, fir = librosa.load('data/air_type1_air_binaural_lecture_0_1.wav',sr = 24000)
#plt.figure()
#plt.subplot(211)
#plt.plot(signal)
#plt.ylabel("Amplitude")
#plt.title("Input signal")
#plt.grid()
#plt.subplot(212)
#plt.plot(ir)
#plt.xlabel('Time/s')
#plt.ylabel("Amplitude")
#plt.title("Room Impulse Response")
#plt.grid()
#plt.show()
return signal, ir
if __name__ == "__main__":
signal,ir = data_read()
output = fft_convolution(signal,ir)
sample_rate = 24000
print(len(output))
plt.figure()
plt.plot(output)
plt.grid()
plt.xlabel('Time/s')
plt.ylabel('Amplitude')
plt.title("Output signal")
plt.show()
path = 'output.wav'
wavfile.write(path,24000,output.astype(np.float32))
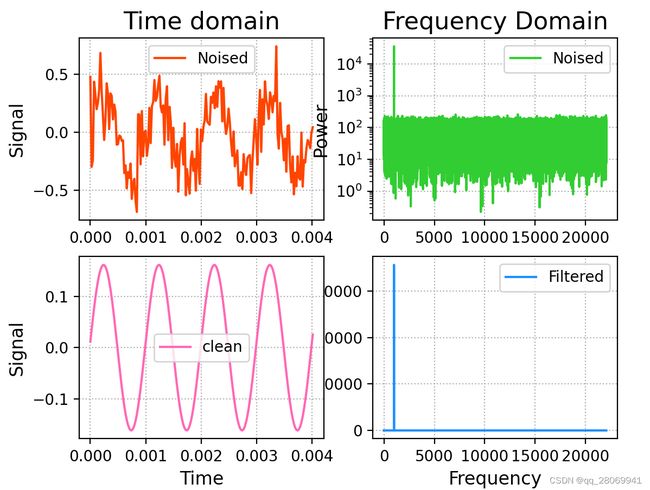
用FFT将信号转换到频域去除能量较低的底噪 (傅里叶变换的应用)
假设此时我们有一个频率的干净信号与一些能量较低的底噪信号相混合的混合信号,我们想要去除掉底噪,得到干净的信号,就可以使用FFT将信号从时域变换到频域进行表示,并在频域寻找其能量最大的值作为我们的干净信号,去除掉那些不等于能量最大的频率,然后再变换回时域,就可以得到干净信号了。
代码如下:
# This script is used to transfer the signal from time domain to
# freqeuncy domain to denoise some noise with low energy
import numpy as np
from scipy.io import wavfile
import matplotlib.pyplot as plt
import librosa
## Read the audio data
noised_sig,sample_rate = librosa.load('data/Signal_with_low_energy_noise.wav',sr = 44100)
times = np.arange(noised_sig.size)/sample_rate; # Use the length of signal over sample rate to get the total time
plt.figure('Filter')
plt.subplot(221)
plt.title('Time domain',fontsize = 16)
plt.ylabel("Signal",fontsize = 12)
plt.tick_params(labelsize = 10)
plt.grid(linestyle= ':')
plt.plot(times[:178],noised_sig[:178],c='orangered',label='Noised')
plt.legend()
## Do the FFT
freqs = np.fft.fftfreq(times.size,times[1]-times[0])
complex_array = np.fft.fft(noised_sig)
pows = np.abs(complex_array)
plt.subplot(222)
plt.title('Frequency Domain',fontsize = 16)
plt.ylabel('Power',fontsize = 12)
plt.tick_params(labelsize = 10)
plt.grid(linestyle = ":")
plt.semilogy(freqs[freqs>0],pows[freqs>0],c='limegreen',label='Noised') # we just want the frequency and power that frequency greater than 0
plt.legend()
## remove the noise with low power and plot in frequency domain
fund_freq = freqs[pows.argmax()]
# Use 'where' function to find the index that we want to remove, that means if the indices is not equal to our frequency with maximal power,
# then these index can be regarded as the index of noise
noised_indices = np.where(freqs!=fund_freq)
filter_complex_array = complex_array.copy()
filter_complex_array[noised_indices] = 0
filter_pows = np.abs(filter_complex_array)
plt.subplot(224)
plt.xlabel('Frequency', fontsize=12)
plt.ylabel('Power', fontsize=12)
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(freqs[freqs >= 0], filter_pows[freqs >= 0], c='dodgerblue', label='Filtered')
plt.legend()
# Used the ifft to transform the signal in frequency domain to time domain
filter_sigs = np.fft.ifft(filter_complex_array).real
plt.subplot(223)
plt.xlabel('Time',fontsize=12)
plt.ylabel('Signal',fontsize = 12)
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(times[:178], filter_sigs[:178], c='hotpink', label='clean')
plt.legend()
# write the new clean signal.
wavfile.write('clean_signal.wav', sample_rate, filter_sigs)
plt.show()
更快的卷积方法(overlap-add和overlap-save)
虽然我们之前用分而治之的思想提出的FFT算法已经能够实现很快的卷积运算了,但是其还是要求我们输入输入信号 x ( n ) x(n) x(n)的全部数据,那么就会有一些问题: 1、如果输入信号 x ( n ) x(n) x(n) 很长,那么此时FFT运算会耗费非常多的内存资源,对于算力较小的机器限制较大。 2、在实际的实时运算当中,我们并没有方法能够得到全部的 x ( n ) x(n) x(n) 数据,所以要考虑分块来进行卷积的方法,比如囤积了512/256/128个数据时,那么就进行一次卷积,这就能够满足实时性的要求,最后再按照相应规则,将子序列的卷积结果拼接起来,就可以得到最后的结果。
Overlap-add
其基本思路是将输入序列 x ( n ) x(n) x(n) 按照时间顺序分割为多段长度为 L L L 的子序列 x k ( n ) x_k(n) xk(n), 并通过计算每个子序列 x k ( n ) x_k(n) xk(n) 与冲激响应 h ( n ) h(n) h(n) 的卷积结果,也就是 y k ( n ) = x k ( n ) ∗ h ( n ) y_k(n) = x_k(n) * h(n) yk(n)=xk(n)∗h(n) ,最终将每个 y k ( n ) y_k(n) yk(n) 按照一定的规律重叠相加,最终可以得到 x ( n ) x(n) x(n) 与 h ( n ) h(n) h(n) 的卷积结果。
推导过程如下:假设脉冲响应 h ( n ) h(n) h(n) 为有限长序列,序列长度为 M M M, 而输入信号序列 x ( n ) x(n) x(n) 为无限长或者序列长度很大的信号序列,那么根据卷积运算的定义,二者之间的卷积计算为:
那么现在我们将输入信号 x ( n ) x(n) x(n)分割为长度为 L L L 的小段,那么就有:
那么原始输入序列 x ( n ) x(n) x(n) 与子序列 x k ( n ) x_k(n) xk(n) 之间的关系就是:
那么现在的 y ( n ) y(n) y(n) 就可以表示为:
又因为卷积运算的线性性质,那么就可以将上式进一步表示为:
也就是:
那么,就可以看到对于此时的输出 y ( n ) y(n) y(n) 可以由 x ( n ) x(n) x(n) 的子序列 x k ( n ) x_k(n) xk(n) 与 h ( n ) h(n) h(n) 的卷积结果 y k ( n ) y_k(n) yk(n) 的叠加得到。所以在这里为了更快的进行卷积运算,还是考虑运用FFT将信号从时域变换到频域进行卷积运算。
其主要算法在于:
- 将长时间输入信号 x ( n ) x(n) x(n)分为块,每个块的大小为2的幂次方(让FFT效率更高),对于最后一个块,采用zero-padding使其大小与其他块相同。
- 将每个块进行FFT变换
- 将脉冲响应(卷积核)也进行FFT变换
- 在频域进行乘积
- 每个块的结果进行IFFT变换,变回到时域
- 将相邻块之间的重叠区域相加,得到最终的输出
# This script is used to implement overlap method to speed up convolution
import time
import numpy as np
from generate_sin_signal import generate_sinusoid
import matplotlib.pyplot as plt
from FFT_convolution import fft_convolution
def overlap_add_convlution(x, h, B = 64, K=None):
M = len(x)
N = len(h)
num_input_blocks = np.ceil(M / B).astype(int)
output_size = M + N - 1
y = np.zeros((output_size,))
for n in range(num_input_blocks):
xb = x[n * B:(n + 1) * B]
u = fft_convolution(xb, h, K)
y[n * B:n * B + len(u)] += u
return y
def test01():
N = 10000
A = 0.8
f0 = 440
fs = 44100
t = 0.02
n = np.arange(0, 0.02, 1 / fs)
phi = 0
x = generate_sinusoid(N, A, f0, fs, phi)
plt.figure()
plt.plot(x)
plt.xlabel('Number')
plt.ylabel('amplitude')
plt.title('sin wave')
plt.show()
return x
def test02():
N = 512
A = 0.8
f0 = 100
fs = 44100
t = 0.02
n = np.arange(0, 0.02, 1 / fs)
phi = 0
x = generate_sinusoid(N, A, f0, fs, phi)
plt.figure()
plt.plot(x)
plt.xlabel('Number')
plt.ylabel('amplitude')
plt.title('sin wave')
plt.show()
return x
if __name__ == "__main__":
x = test01() # generate the sin signal with frequency 440Hz
h = test02()
a = time.perf_counter()
y = np.convolve(x,h)
b = time.perf_counter()
t1 = b-a
print("使用numpy的convolve所花时间为%f" %t1)
c = time.perf_counter()
y2 = overlap_add_convlution(x,h)
d = time.perf_counter()
t2 =d -c
print("使用overlap-add所花时间为%f" % t2)
Overlap-save
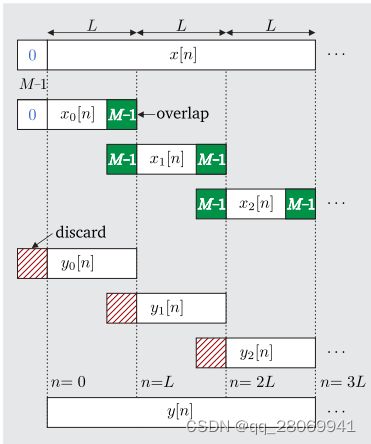
其基本思路核overlap-add方法相似,也是将 x ( n ) x(n) x(n) 在时间上分割成等长的子序列 x k ( n ) x_k(n) xk(n),计算每个子序列 x k ( n ) x_k(n) xk(n)与 h ( n ) h(n) h(n)的卷积结果 y k ( n ) = x k ( n ) ∗ h ( n ) y_k(n) = x_k(n)*h(n) yk(n)=xk(n)∗h(n),不同之处在于 :其将每个 y k ( n ) y_k(n) yk(n) 按照一定的规律保留其中某些项,丢弃另外项,组成 y ( n ) y(n) y(n) ,与OLA不同的是,OLS选取的分割长度为 L + M − 1 L+M-1 L+M−1。并且这种算法算出的输出区块并不重叠(计算上少了将输出区块相加所需的加法运算),而是每次使用的输入区块有所重叠,因此实现时每次读取输入后需将核下一个输入重叠的部分存储起来,作为下一输入区块的开头部分。
那么按照上面的规则,那么我们可以对序列 x ( n ) x(n) x(n) 进行分段:
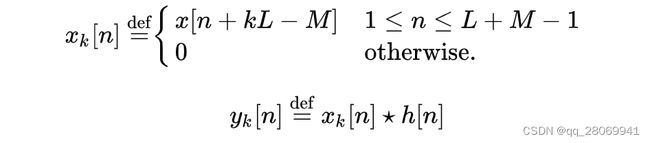
那么在区间 [ k L + 1 , ( k + 1 ) L ] [kL+1,(k+1)L] [kL+1,(k+1)L]内的n,输出 y ( n ) y(n) y(n) 可以表示为:
![]()
那么我们只需要计算 n n n 在 [ M + 1 , L + M ] [M+1,L+M] [M+1,L+M]的 y k [ n ] y_k[n] yk[n] 部分即可。因此每一段输出区块 y k [ n ] y_k[n] yk[n] 的前 M − 1 M-1 M−1个点可以丢弃(discard),保留剩余 L L L 点的数值。
如果此时我们将 x k [ n ] x_k[n] xk[n]做 N ≥ L + M − 1 N\geq L+M-1 N≥L+M−1 的周期延拓,
那么 x k , N ∗ h x_{k,N}*h xk,N∗h和 x k ∗ h x_k*h xk∗h这两个卷积在 [ M + 1 , L + M ] [M+1,L+M] [M+1,L+M]的部分相等,所以可以将线性卷积变成 N N N 点的循环卷积进行计算。结果的 [ M + 1 , L + M ] [M+1,L+M] [M+1,L+M] 部分作为输出 y [ n ] y[n] y[n]在 [ M + 1 , L + M ] [M+1,L+M] [M+1,L+M] 的部分。那么由于循环卷积定理,两个离散序列的循环卷积的傅里叶变换等于这两个序列在频域内的点积。
y k [ n ] = I F F T ( F F T ( x k [ n ] ) ⋅ F F T ( h [ n ] ) ) y_k[n] = IFFT(FFT(x_k[n])\cdot FFT (h[n])) yk[n]=IFFT(FFT(xk[n])⋅FFT(h[n]))
那么此时就可以变成三次 N N N点快速傅里叶变换和 N N N 次乘法,使得原本每段 O ( N 2 ) O(N^2) O(N2)的运算量减少至 O ( N l o g N ) O(NlogN) O(NlogN),可以提升很高的运算速度。
def overlap_save_convolution(x,h,B,K=None):
M = len(x)
N = len(h)
if K is None:
K = next_power_of_2(B+N-1)
# Calculate the number of input blocks
num_input_blocks = np.ceil(M/B).astype(int) + np.ceil(K/B).astype(int) - 1
# pad zeros
xp = pad_zeros_to(x,num_input_blocks*B)
output_size = num_input_blocks * B+N-1
y = np.zeros((output_size,))
# input buffer
xw = np.zeros((K,))
# Convolve all blocks
for n in range(num_input_blocks):
# Extract the n-th input block
xb = xp[n*B:n*B+B]
# Sliding window of the input
xw = np.roll(xw,-B)
xw[-B:] = xb
# FFT
u = fft_convolution(xw,h,K)
# Save the valid output samples
y[n*B:n*B+B] = u[-B:]
return y[:M+N-1]
5、短时傅里叶变换 STFT
短时傅里叶变换是什么?我们为什么要用它?
在我们之前所介绍的傅里叶变换等都是针对平稳信号的,但是在很多实际应用中的信号均为非平稳的,如果要计算其傅里叶变换,需要假设其周期无限长,然后对这个无限长的信号做变换分析。但是我们在实际过程中并不能实现这种无限长信号的分析,我们只能对有限长的局部信号进行分析,且被分析的有限长局部信号需满足两个条件:1、信号在截取这段时间内是平稳的 。2、在局部平稳信号中包含至少1个完整的周期。
因此我们可以考虑截取非平稳信号的局部平稳信号,然后采用傅里叶变换进行频域分析,这种方法便就是短时傅里叶变换。
什么是平稳信号:
随机信号是随机过程,其每个时间点都是随机变量,随机变量并没有确定值,只有在每次观测过程中得到的一组观测值,那么我们只能通过对随机变量进行统计观测,才能对其的概率分布进行估计。所以对于随机信号来说,无论是否平稳,我们都从其的统计学特性来考虑。
平稳信号包含的信息量小,其统计特性不随时间变化,统计特性不变,也就是说在对平稳随机信号进行一定的时间观测后,就不需要其后续的观测了,因为此时信号的全部统计信息已经被获得了。平稳随机信号在不同时刻的期望值相同,或者表达成为其自相关函数只与时间间隔相关。也就是可以把平稳随机信号看作为在直流信号上加上看似随机波动的波形。比如直流加白噪声。
而对于非平稳随机信号,其统计特性随着时间在变,其信息量是变化的,始终会有“新息”引入,而“新息”主要指的就是当前信号的值与预测信号值的差值。预测信号是根据过去信号的统计特性推测出来的,“新息”具有不可预测的部分。如f(t) = t这个确定信号叠加白噪声,其就是非平稳信号。而对于语音信号来说,有时是短时平稳(人声的浊声),但是总体呈现的是非平稳的。[1]对于平稳随机信号,比较显著的就是高斯噪声。
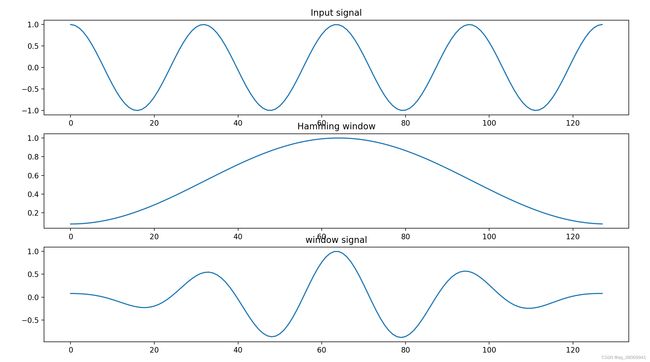
然而,在我们截取原始的非平稳信号时,如果信号截断为非周期截断,那么频谱将发生泄漏,所以通过引入一种窗函数,通过加窗,可以减少频谱的泄漏,换句话来说,也就是窗函数可以将一个非周期的信号,强行转变为一个周期信号。在时域加窗表现为信号与窗函数的点乘,而在频域表示为信号的卷积。假设时域信号为 x x x,生成窗函数为 w w w,那么加窗后的信号为 x = x ⋅ w x = x\cdot w x=x⋅w。
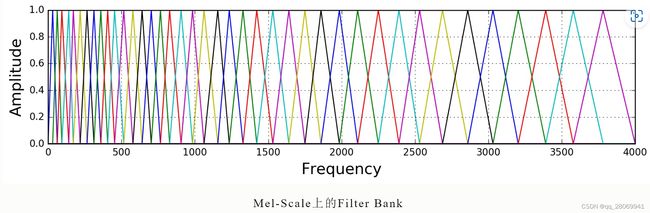
窗函数
上图便是对于窗函数的一个演示,即对一个 c o s cos cos 信号加上 h a m m i n g hamming hamming 窗,其代码如下:
### This script is used implement the window function
import numpy as np
from scipy.signal import get_window
import matplotlib.pyplot as plt
M = 128 # The length of signal
x = np.cos(np.linspace(0,8*np.pi,128)) # Generate cos signal
w = get_window('hamming',M) # call the window function , generate w (hamming window)
xw = x*w
plt.figure()
plt.subplot(311)
plt.plot(x)
plt.title('Input signal')
plt.subplot(312)
plt.plot(w)
plt.title("Hamming window")
plt.subplot(313)
plt.plot(xw)
plt.title("window signal")
plt.show()
那么在前一节提到了,窗函数是被用来削弱我们对非平稳信号非周期截断时引起的频谱泄漏,那么频谱泄漏就可以理解为,我们对信号进行非周期截断,截断后的信号起始时刻和结束时刻的幅值明显不等,我们再对这个信号进行重构时,再连接处信号的幅值不连续,出现跳跃。那么变换到频域上也就是说,这个频点的能量泄漏到了旁边其他频率上去,造成了频谱的在频带上的拖尾现象,关于频谱泄漏的进一步解释可以参考这篇文章:什么是泄漏? (qq.com)。
通过代码生成了一段 c o s cos cos信号,并观察加窗后对其在频谱的频谱泄漏的抑制情况。
## This script is used to demonstrate what is frequency leakage
import numpy as np
from scipy.signal import get_window
from scipy.fftpack import fft
import matplotlib.pyplot as plt
M = 128 # The length of signal
x = np.cos(np.linspace(0,100*np.pi,128)) # Generate cos signal
w = get_window('hamming',M) # call the window function , generate w (hamming window)
X = fft(x)
mX = np.abs(X)
xw = x*w
XW = fft(xw)
mXW = np.abs(XW)
plt.subplot(221)
plt.plot(x);plt.title('(a)Input signal')
plt.subplot(222)
plt.plot(xw);plt.title('(b)Windowed signal')
plt.subplot(223)
plt.plot(mX);plt.title('(c)Amplitude of unwindowed signal')
plt.subplot(224)
plt.plot(mXW);plt.title('(d)Amplitude of windowed signal')
plt.show()
对于窗函数的要求:一个理想的窗函数在频域的主瓣应该非常窄,有足够的频率分辨率。而旁瓣又能尽可能低,使得对其余频点的能量泄漏尽可能少。但是在实际中,我们不能同时坐到主瓣和旁瓣性能最优,需要在这两者之间取得一个性能的折中。常见的窗函数有矩形窗,Hanning,Hamming,Blackman,Chebyshev等。我们常用 s c i p y . s i g n a l scipy.signal scipy.signal 中的 g e t − w i n d o w get -window get−window 来生成窗函数。 详情可以看scipy.signal.get_window — SciPy v1.10.1 Manual
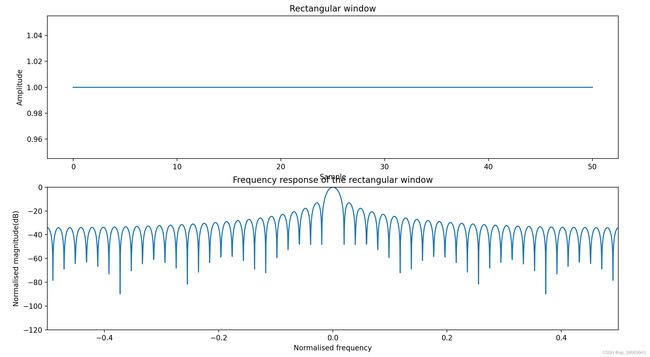
矩形窗:
主瓣集中,频率分辨率较高,但是旁瓣较高,主瓣宽度:2bins, 旁瓣高度:-13.3dB
代码如下:
### This script is used to implement the rectangular window function
import numpy as np
from scipy.signal import get_window
from scipy import signal
from scipy.fftpack import fft,fftshift
import matplotlib.pyplot as plt
w = signal.boxcar(51)
W = fft(w,2048)
freq = np.linspace(-0.5,0.5,len(W))
response = 20*np.log10(np.abs(fftshift(W/np.abs(W).max())))
plt.figure()
plt.subplot(211)
plt.plot(w)
plt.title('Rectangular window')
plt.ylabel('Amplitude')
plt.xlabel('Sample')
plt.subplot(212)
plt.plot(freq,response)
plt.axis([-0.5,0.5,-120,0])
plt.title('Frequency response of the rectangular window')
plt.ylabel('Normalised magnitude(dB)')
plt.xlabel('Normalised frequency')
plt.show()
Hanning窗(升余弦窗)
主瓣更宽,频率分辨率下降,旁瓣减小,频谱泄漏减小。 主瓣宽度:4bins, 旁瓣高度:-31.5dB
### This script is used to implement the rectangular window function
import numpy as np
from scipy.signal import get_window
from scipy import signal
from scipy.fftpack import fft,fftshift
import matplotlib.pyplot as plt
w = signal.hanning(51)
W = fft(w,2048)
freq = np.linspace(-0.5,0.5,len(W))
response = 20*np.log10(np.abs(fftshift(W/np.abs(W).max())))
plt.figure()
plt.subplot(211)
plt.plot(w)
plt.title('Hanning window')
plt.ylabel('Amplitude')
plt.xlabel('Sample')
plt.subplot(212)
plt.plot(freq,response)
plt.axis([-0.5,0.5,-120,0])
plt.title('Frequency response of the hanning window')
plt.ylabel('Normalised magnitude(dB)')
plt.xlabel('Normalised frequency')
plt.show()
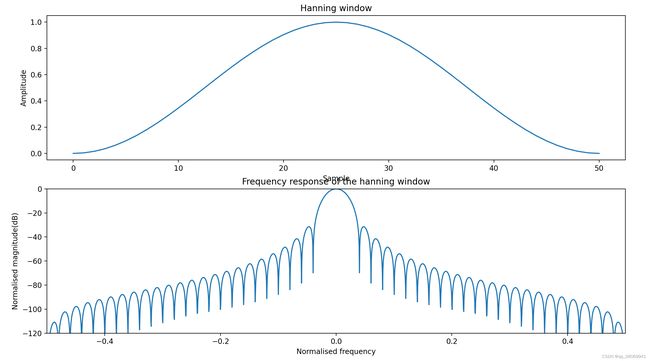
Hamming: 改进升余弦窗
相对Hanning窗来说,旁瓣更小,但是旁瓣衰减速度变慢。主瓣宽度:4bins, 旁瓣高度:-42.7dB
w [ n ] = 0.54 + 0.46 ∗ c o s ( 2 π n / M ) w[n] = 0.54 + 0.46 * cos(2\pi n /M) w[n]=0.54+0.46∗cos(2πn/M)
### This script is used to implement the rectangular window function
import numpy as np
from scipy.signal import get_window
from scipy import signal
from scipy.fftpack import fft,fftshift
import matplotlib.pyplot as plt
w = signal.hamming(51)
W = fft(w,2048)
freq = np.linspace(-0.5,0.5,len(W))
response = 20*np.log10(np.abs(fftshift(W/np.abs(W).max())))
plt.figure()
plt.subplot(211)
plt.plot(w)
plt.title('Hamming window')
plt.ylabel('Amplitude')
plt.xlabel('Sample')
plt.subplot(212)
plt.plot(freq,response)
plt.axis([-0.5,0.5,-120,0])
plt.title('Frequency response of the hamming window')
plt.ylabel('Normalised magnitude(dB)')
plt.xlabel('Normalised frequency')
plt.show()
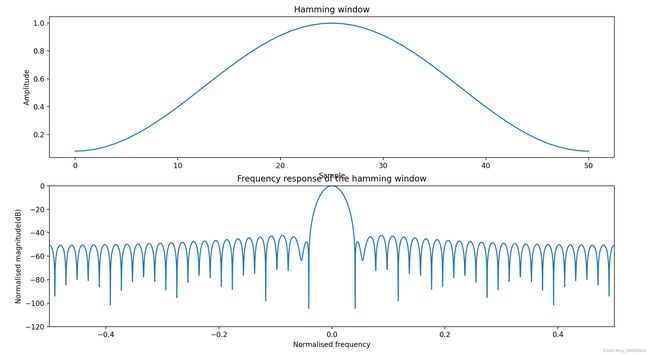
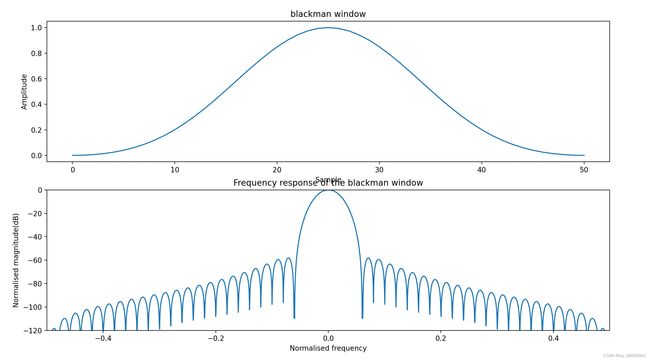
Blackman窗(二阶升余弦窗)
主瓣宽,旁瓣比较低。主瓣宽度:6bins, 旁瓣高度:-58dB
w [ n ] = 0.42 − 0.5 c o s ( 2 π n / M ) + 0.08 c o s ( 4 π n / M ) w[n] = 0.42- 0.5 cos(2\pi n /M) + 0.08 cos(4 \pi n /M) w[n]=0.42−0.5cos(2πn/M)+0.08cos(4πn/M)
### This script is used to implement the rectangular window function
import numpy as np
from scipy.signal import get_window
from scipy import signal
from scipy.fftpack import fft,fftshift
import matplotlib.pyplot as plt
w = signal.blackman(51)
W = fft(w,2048)
freq = np.linspace(-0.5,0.5,len(W))
response = 20*np.log10(np.abs(fftshift(W/np.abs(W).max())))
plt.figure()
plt.subplot(211)
plt.plot(w)
plt.title('blackman window')
plt.ylabel('Amplitude')
plt.xlabel('Sample')
plt.subplot(212)
plt.plot(freq,response)
plt.axis([-0.5,0.5,-120,0])
plt.title('Frequency response of the blackman window')
plt.ylabel('Normalised magnitude(dB)')
plt.xlabel('Normalised frequency')
plt.show()
STFT的原理及实现:
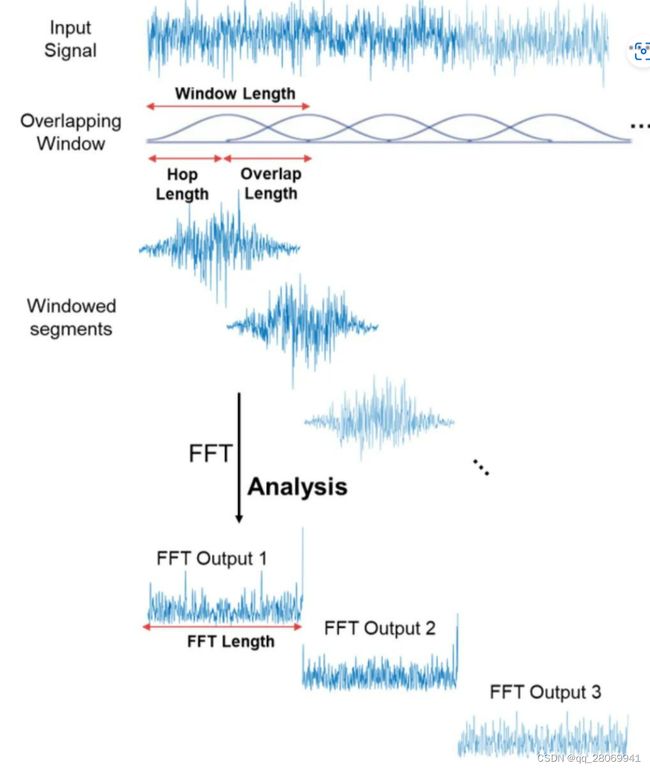
关于STFT的原理,可以参考这篇文章:STFT(短时傅里叶变换)的原理与使用 - 知乎 (zhihu.com),在短时傅里叶变换过程中,窗的长度决定频谱的时间分辨率和频率分辨率,窗长越长,截取的信号越长,信号越长,傅里叶变换后的频率分辨率越高,时间分辨率越差,相反,窗长越短,截取的信号就越短,频率分辨率越差,时间分辨率就越好,也就是说,在短时傅里叶变换中,时间分辨率和频率分辨率不能兼得,只能在中间根据具体需求取得一个折中。 原理可以看下方图片:
计算短时傅里叶变换,我们需要指定的参数有:
- 每个窗口的长度: w i n win win_ l e n g t h length length
- 每相邻两个窗口的重叠率: h o p hop hop_ l e n g t h length length
- 每个窗口的FFT采样点数: n n n_ f f t fft fft
- 窗函数: w w w
- 信号被分成了多少片
- spectrogram
关于STFT的实现,我们可以使用 l i b r o s a . s t f t librosa.stft librosa.stft 来计算
librosa.stft(y, n_fft=2048, hop_length=None, win_length=None, window='hann', center=True, pad_mode='reflect')
其中的参数:
- y y y: 输入音频序列
- n n n_ f f t fft fft: FFT 窗口大小, :n_fft = hop_length + overlapping
- hop_length : 帧移, 若未指定,一般默认为 win_length/4
- win_length: 分割好的每一帧音频都由window()加窗。 窗长 win_length, 并zero-padding 来匹配 n_fft,默认win_length = n_fft
- window: 指定窗函数具体参数
- center: bool
- 如果为True, 则填充信号y,以使帧D[:,t] 以 y[t * hop_length ]为中心
- 如果为False, 则D[:,t] 以 y[t * hop_length] 开始
- pad_mode: 如果center = true, 那么在信号边缘用填充模式, 默认情况下使用 reflection padding
返回值:
- STFT 矩阵 D, shape = (1+ n f f t 2 , t \frac{n_{fft}}{2},t 2nfft,t)
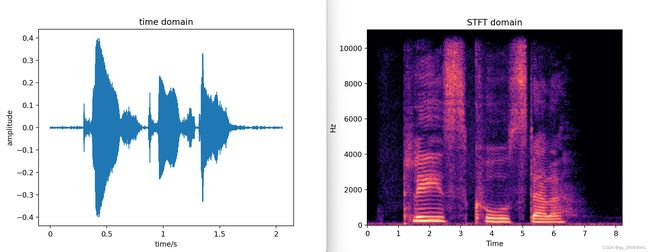
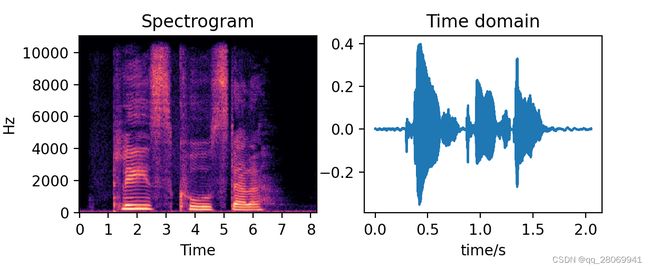
对于语音"Please call Stella" 的time domain 和 STFT domain 图和code如下:
## This script is used to transfer the signal from time domain into STFT domain
import numpy as np
import librosa
import matplotlib.pyplot as plt
import librosa.display
signal, sample_rate = librosa.load('[email protected]')
D = librosa.stft(signal,n_fft = 512, hop_length = None, win_length = None, window = 'hann',center = True, pad_mode = 'reflect')
print(D.shape)
# divide into magnitude and phase
magnitude, phase = librosa.magphase(D, power= 1)
angle = np.angle(phase)
# plot the time domain and stft domain
plt.figure()
# time domain
librosa.display.waveshow(signal,sample_rate)
plt.xlabel('time/s')
plt.ylabel('amplitude')
plt.title('time domain')
# STFT domain
plt.figure()
STFT = librosa.amplitude_to_db(np.abs(D),ref= np.max)
img = librosa.display.specshow(STFT,sr = sample_rate, x_axis = 'time',y_axis = 'linear')
plt.title('STFT domain')
plt.show()
Mel频谱以及Mel倒谱系数(MFCC)
在上一节当中,我们通过STFT将语音信号从时域变换到了STFT域,并且得到了对应的spectrogram, 频谱表示频率和能量的关系,通过观察功率谱可以清晰的看到语音信号中的共振峰等语音特征,其在语音识别等领域有很好的作用,但是因为频谱图是一个包含有原始信号信息的频域表示,为了尽量减少数据大小,降低计算复杂度,得到合适大小的声音特征,我们往往将其通过梅尔标度滤波器组(mel-scale filter banks)变换为梅尔频谱,那么什么是梅尔滤波器组呢,这要从mel标度说起:
其基本思想与判断相同响度相同,mel 刻度是一种由听众判断不同频率的音高(pitch) 彼此相等的感知刻度,表示人耳对等距音高变化的感知,通俗点来说就是,人耳对频率的感知并不是线性的,我们的基底膜对低频信号彼此的区别更加敏感,对高频信号的区别不是那么敏感,也就是低频段上的两个频度和高频段的两个频度,人们更容易区分前者,频域上相等距离的两对频度,对人耳来说距离并不相等。例如:我们先听1000Hz的声音,如果我们把频率提高到2000Hz,那么我们的耳朵也只能觉察到频率提高了一点点,并不能觉察到频率提高了一倍。所以Mel刻度就被提出了,其用来调整频域的刻度,使得在这个刻度上相等距离的两对频度,在人耳感知中也相同。Mel 刻度和正常频率(Hz)之间的参考点是将1kHz,且高于人耳听阈值40dB以上的基音,定为1000mel。在大约500Hz以上,听者判断越来越大的音程产生相等的音调增量,然后最后发现,人耳感觉到的等量的音高变化,所需要的频率变化随频率增大而越来越大。
运用梅尔频谱可以将语音信号从线性频域转换到感知频域中,能够更好的模拟听觉过程的处理。
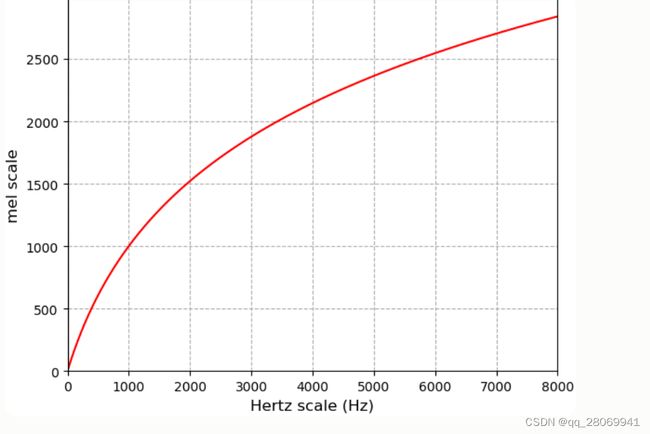
将频率 f ( H z ) f(Hz) f(Hz) 转换到mel m m m 的公式为:
M = 2595 l o g 10 ( 1 + f 700 ) M = 2595log_{10}(1+\frac{f}{700}) M=2595log10(1+700f)
将梅尔 m m m 转换到频率 f ( H z ) f(Hz) f(Hz) 的公式为:
f = 700 e m 2595 − 1 f = 700e^{\frac{m}{2595}-1} f=700e2595m−1
我们主要进行的处理就是:把进入人耳的声音频率用临界频带(critical Band) 进行划分,将语音在频域上划分为一系列的频率群,构成一个Mel滤波器组,因为人耳对不同频率的声波有敏感度,因为频率较低的声音在基底膜上行波传递距离大于频率较高的声音,因此低音容易掩蔽高音,且低音掩蔽的临界带宽相较高频小,所以研究人员从低频到高频按照临界频带的大小由密到疏设计了一组带通滤波器, 对输入信号进行滤波,将每个带通滤波器输出的信号能量作为信号的基本特征,对此特征经过进一步处理后得到语音的输入特征。
什么是临界频带: 耳蜗的基底膜上有24个点能对24个不同频率产生最大幅度共振,从而将人耳可听频率范围 20 H z − 22 k H z 20Hz - 22kHz 20Hz−22kHz 分为24个频带,即为临界频带。
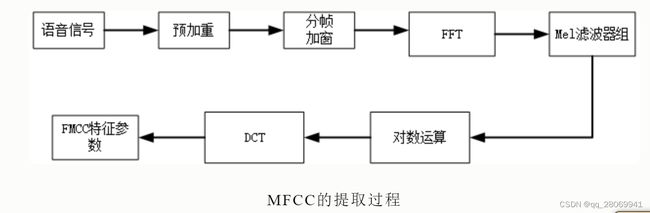
求MFCC的步骤:
- 分帧、加窗
- 对于每一帧,计算功率谱的周期图估计
- 将mel滤波器组应用于功率谱,求滤波器组的能量,将每个滤波器中的能量相加
- 取所有滤波器组能量的对数
- 取对数滤波器组能量的离散余弦变换(DCT)。
- 保持DCT系数2-13,其余部分丢弃
1、预处理
在这里预处理主要包括预加重、分帧、加窗。我们还是采用语音信号"Please call stella"
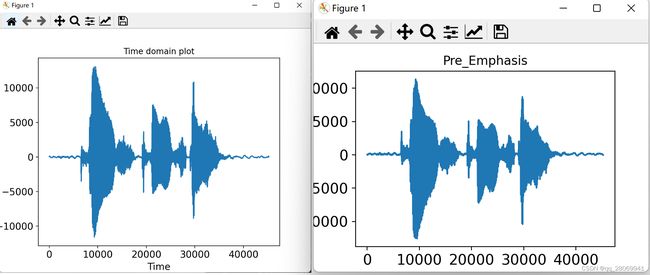
① 预加重
我们对信号应用预加重滤波器来放大高频,主要是为了
- 平衡频谱,因为高频声相较于低频声有较小幅度
- 改善信噪比(SNR)
- 消除发生过程中声带和嘴唇带来的高频抑制,突出高频的共振峰
预加重就是将一个高通滤波器作用在语音信号上, 这里用:
y ( t ) = x ( t ) − α x ( t − 1 ) y(t) = x(t) - \alpha x(t-1) y(t)=x(t)−αx(t−1)
其中滤波器系数( α \alpha α) 通常取0.95或者0.97,下图为原始信号和加重后的信号对比。
②、分帧
和之前在STFT介绍的一样,因为语音信号是非平稳信号,我们不能直接对其使用DFT,所以考虑将信号分帧称为短时平稳信号,并
在短帧上进行傅里叶变换,我们将截取20-40ms的帧,一般采用frame_size = 0.025s。帧移通常设置为10ms, frame_stride = 0.01,为了避免相邻两帧的变化过大,我们让两个相邻的帧之间有一段重叠的区域,一般为每帧的1/2或者1/3,我们设置overlap = 0.015s (15ms), 如果没有划分为偶数个数的帧,那么就用zero-padding。
③、加窗 (window)
原理和STFT节中所提及相同,为了平滑截断所造成的不连续性,引入了窗函数,详细说明请往前翻
2、FFT
之后对每个加窗后的信号帧用FFT转换到频域来计算频谱,其中NFFT = 512
3、功率谱
之后运用以下公式计算信号的功率谱,对语音信号的频谱取模平方
P = ∣ F F T ( x i ) ∣ 2 N P = \frac{|FFT(x_i)|^2}{N} P=N∣FFT(xi)∣2
4、Mel 刻度滤波器组
将功率谱通过一组Mel刻度(通常为40个滤波器,nfilt = 40) 的三角滤波器组来提取频带,低频处滤波器密集,门限值大,高频处滤波器稀疏,门限值低。正好能够模拟人耳对声音的非线性感知,对较低的频率有更强的辨别力。
滤波器组中的每个滤波器都是三角形的,中心频率为f(m),中心频率处的响应为1,并向0线性减小,直到达到两个相邻滤波器的中心频率,其中此处响应为0,各f(m)之间的间隔随着 m m m 值得增大而变宽。
三角形滤波器的频率响应为:
![]()
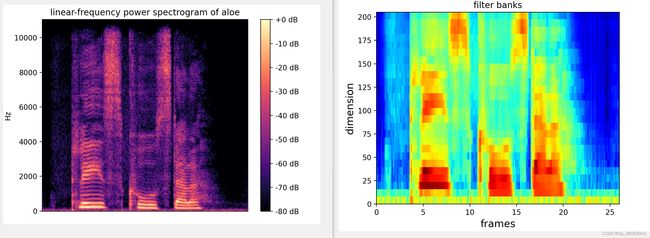
对于我们刚刚STFT得到的幅度谱,我们将其分别跟每一个滤波器进行频率相乘累加,得到的值就是该帧数据在该滤波器对应的频段的能量值。如果滤波器的个数为40,那么就应该得到40个能量值。
那么可以看到信号的功率谱经过滤波器组后,得到的频谱图和原始频谱图的对比
5、Mel 频率倒谱系数(MFCC)
在实际应用中,在上一节中计算的滤波器组系数是高度相关的,在一些机器学习算法中会有一些问题,所以我们可以应用离散余弦变换(DCT)对滤波器组系数去相关处理,得到滤波器组的压缩表示(这一块和稀疏感知相关)。对于自动语音识别技术(ASR),一般保留所得到的倒谱系数个数为2~13之间,并丢弃其余部分(丢弃的这部分系数会代表滤波器组系数的快速变化,这种精细的特征对ASR无帮助,故舍弃)。我们这里考虑num_ceps = 12。 (注意使用DCT有很大限制:因为DCT是一种线性变换,在语音信号中丢弃一些高度非线性的信息是不可取的。)
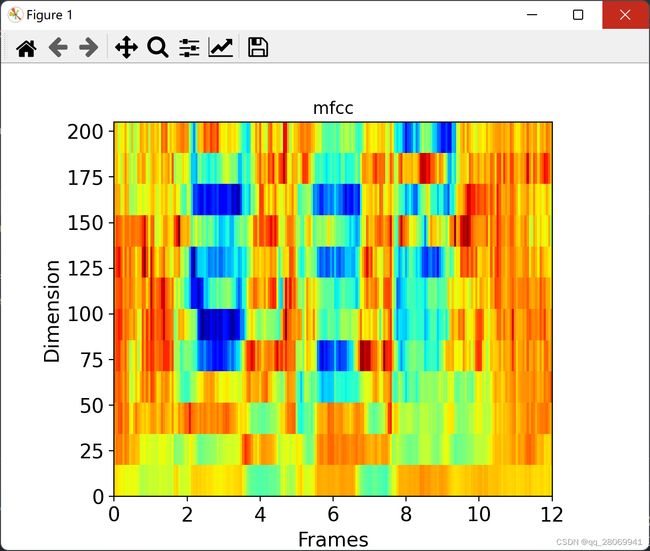
C ( n ) = ∑ m = 0 N − 1 s ( m ) c o s ( π n ( m − 0.5 ) M ) , n = 1 , 2 , . . . . , L C(n) = \sum_{m=0}^{N-1}s(m)cos(\frac{\pi n(m-0.5)}{M}), n = 1,2,....,L C(n)=m=0∑N−1s(m)cos(Mπn(m−0.5)),n=1,2,....,L
这是所得到的MFCC:
使用方法
Python 可以调用 l i b r o s a librosa librosa库直接提取Mel频谱和MFCC:
mel_spec = librosa.feature.melspectrogram(y=y, sr=sr, n_mels=128, fmax=8000)
mfccs = librosa.feature.mfcc(y=y, sr=sr, n_mfcc=40)
下面是上述理论过程的一个代码实现和总结
## 这个代码是用来熟悉mfcc的
import librosa
import librosa.display
import matplotlib.pyplot as plt
import numpy as np
from scipy.fft import dct
# 读取音频代码1,利用librosa库来读取
data1, sampling_rate1 = librosa.load('[email protected]')
# 读取音频代码2
# from scipy.io import wavfile
# sample_rate, signal = wavfile.read('[email protected]')
# 查看波形图
plt.figure()
librosa.display.waveshow(data1*32767,sr=sampling_rate1) # librosa模块读取音频进行了归一化处理
plt.show()
# 查看声谱图
# 声谱图是声音或其他信号的频率随时间变化时的频谱(spectrum)的表示
D = librosa.amplitude_to_db(np.abs(librosa.stft(data1,n_fft = 512)),ref=np.max) # 这里取librosa里的stft并用绝对值表示,ref用np的最大值
librosa.display.specshow(D,y_axis = 'linear')
plt.colorbar(format = '%+2.0f dB')
plt.title('linear-frequency power spectrogram of aloe')
plt.show()
## 梅尔倒谱系数的定义
# 人耳对声音信号的感知聚焦在某一特定频率区域内,而并非在整个频谱包络中,耳蜗的滤波作用是在对数频率尺度下的
# 其在1000Hz以下为线性,1000以上为对数,人耳对低频比高频更敏感
# 人类对语音信号的频率内容的感知遵循主观定义的非线性尺度,其被称为'Mel'尺度
# Mel是音调的单位,其反应出了频率与音调的非线性关系
# MFCC将人耳的听觉感知特性和语音产生机制结合,主要在于对频率轴不均匀的划分
# Mel带通滤波器组的中心频率是按照Mel刻度均匀排列的。
# 滤波器集中在低频部分,在高频部分滤波器较少
# MFCC的主要步骤
# 对语音信号进行预加重、分帧和加窗处理
# 对语音信号进行短时傅里叶变换 (短时傅里叶变换)
# 对功率谱用mel滤波器组进行滤波,计算每个滤波器里的能量(梅尔频谱)
# 然后对梅尔频谱进行取对数(log梅尔频谱)
# 再对其进行离散余弦变换,(梅尔倒谱)
# 保留变换后的2-13个系数,去掉其他的(MFCC特征)
# 预加重,分帧和加窗
# 1、读取音频
signal, sample_rate = librosa.load('[email protected]')
signal *= 32767 # 因为librosa中读取的音频信号为归一化的信号,所以乘上32767还原信号原始幅值
print(len(signal))
axis_x = np.arange(0,signal.size,1)
plt.plot(axis_x,signal)
plt.title('Time domain plot')
plt.xlabel('Time',fontsize=14)
plt.ylabel('Amplitude',fontsize=14)
plt.tick_params(axis='both',labelsize=14)
plt.show()
# 2、预加重
# 是为了放大高频,因为高频通常比低频有更小的幅值
# 避免在傅里叶变换过程中出现数值问题
# 改善信号信噪比(SNR)
# 用一阶滤波器应用在信号上 典型值为0.95或0.97
pre_emphasis = 0.97
emphasized_signal = np.append(signal[0],signal[1]-pre_emphasis*signal[:-1])
axis_x = np.arange(0,emphasized_signal.size,1)
plt.plot(axis_x,emphasized_signal)
plt.title('Pre_Emphasis')
plt.xlabel('time',fontsize=14)
plt.ylabel('Amplitude',fontsize=14)
plt.tick_params(axis='both',labelsize=14)
plt.show()
# 3、分帧
# 经过预加重后,要将信号分成短帧,因为信号中的频率会随时间变化,所以不能对整段信号进行傅里叶变换
# 假设信号的频率在很短的时间段内固定的,在短帧上进行傅里叶变换,并串联相邻帧来获得信号频率轮廓较好的近似
# 在语音信号处理中典型帧长度为20ms——40ms,并且连续帧之间有50%的overlap,设定帧为25ms,并且重叠15ms,帧移为10ms
frame_stride = 0.01 # 帧移为10ms
frame_size = 0.025 # 帧长为25ms
frame_length = frame_size * sample_rate # 计算所有的采样点的总共帧长
frame_step = frame_stride * sample_rate # 计算所有采样点的总共帧移
signal_length = len(emphasized_signal)
frame_length = int(round(frame_length))
frame_step = int(round(frame_step))
# 向上取整求最后帧的数量,用信号长度减去帧长度再加上帧移长度除以帧移长度
num_frames = int(np.ceil(float(np.abs(signal_length-frame_length+frame_step))/frame_step))
# 又因为信号长度可能不是帧长整数倍,对原信号进行填充,至帧长的整数倍
pad_signal_length = (num_frames - 1)* frame_step+frame_length
z = np.zeros((pad_signal_length - signal_length))
pad_signal = np.append(emphasized_signal,z)
# 之后将音频信号转化为二维矩阵,每一行就是一个音频帧的内容
indices = np.tile(np.arange(0,frame_length),(num_frames,1))+np.tile(np.arange(0,num_frames*frame_step,frame_step),(frame_length,1)).T
print(indices.shape)
# 将补零后的信号转换为num_frames*frame_length的格式
frames = pad_signal[indices.astype(np.int32,copy=False)]
# 4、加窗
# 将信号切成帧后,对每个帧应用窗函数,抵消FFT的无限计算并减少频谱泄露
frames = frames*np.hamming(frame_length)
# 5、STFT,对每个帧上执行N点FFT来计算频谱,N通常为256或512
NFFT = 512
mag_frames = np.abs(np.fft.rfft(frames,NFFT))
pow_frames = ((1.0/NFFT)*((mag_frames)**2))
# 6、对功率谱用Mel滤波器组进行滤波,计算每个滤波器里的能量,并对每个滤波器能量取log
# 因为声谱图中包含了许多无用的信息,我们用梅尔标度滤波器组将其变换为更简洁的梅尔频谱
# 梅尔尺度建立了从人类的听觉感知频率,也就是声调到声音直接频率的映射,因为人耳对Hz并不是线性感知关系
# 人耳对低频音调更敏感,而高频迟钝
# 梅尔滤波器组用26个三角滤波器组组成,对上一步得到的STFT进行滤波,并且区间频率越高,滤波器就越宽
# 将26个滤波器用一个矩阵表示,有26行
nfilt = 26
low_freq_mel = 0
high_freq_mel = (2595*np.log10(1+(sample_rate/2)/700)) # 从HZ转到mel
mel_points = np.linspace(low_freq_mel,high_freq_mel,nfilt+2) # 这里划分nfilt+2个区域,因为一个三角滤波器实际上要占3个刻度
hz_points = (700 * (10**(mel_points/2595)-1)) # 从mel转到hz
bin = np.floor((NFFT+1)*hz_points/sample_rate) # bin是响应的傅里叶变换点数
# fbank的shape是26*257,来储存每个滤波器的值
fbank = np.zeros((nfilt,int(np.floor(NFFT/2+1))))
print(fbank.shape)
for m in range(1,nfilt+1):
f_m_minus = int(bin[m-1])
f_m = int(bin[m])
f_m_plus = int(bin[m+1])
for k in range(f_m_minus,f_m):
fbank[m-1,k]=(k-bin[m-1])/(bin[m]-bin[m-1])
for k in range(f_m,f_m_plus):
fbank[m-1,k]=(bin[m+1]-k)/(bin[m+1]-bin[m])
# 将功率谱与滤波器做点积
filter_banks = np.dot(pow_frames,fbank.T)
filter_banks = np.where(filter_banks ==0,np.finfo(float).eps,filter_banks)
filter_banks = 20*np.log10(filter_banks)
plt.title('filter banks')
plt.imshow(np.flipud(filter_banks.T),cmap=plt.cm.jet,aspect=0.1,extent=[0,filter_banks.shape[1],0,filter_banks.shape[0]])
plt.xlabel("frames",fontsize=14)
plt.ylabel('dimension',fontsize=14)
plt.show()
# 梅尔倒谱MFCCs,利用离散余弦变换,保留DCT的2-13个系数,产生滤波器组的压缩表示,丢弃的系数代表滤波器系数的快速变化,不太重要
num_ceps = 12
mfcc = dct(filter_banks,type=2,axis=1,norm='ortho')[:,1:(num_ceps+1)] # 保留
cep_filter = 22
(nframes,ncoeff)=mfcc.shape
n = np.arange(ncoeff)
lift = 1+(cep_filter/2)*np.sin(np.pi*n/cep_filter)
mfcc=lift*mfcc
plt.title('mfcc')
plt.imshow(np.flipud(mfcc.T), cmap=plt.cm.jet, aspect=0.05, extent=[0, mfcc.shape[1], 0, mfcc.shape[0]]) # 画热力图
plt.xlabel("Frames", fontsize=14)
plt.ylabel("Dimension", fontsize=14)
plt.tick_params(axis='both', labelsize=14)
plt.show()
6、语音数据增强
我们在这里考虑对语音做一些增强,也就是对数据做一些较小的改动,主要是在于
- Noise addition (增加噪音)
- Reverberation addition (增加混响)
- Time shifting (时移)
- Pitch shifting (改变音调)
- Time stretching (拉伸时间)
一、导入原始语音数据
#This script is used to do some simple speech enhancement
import numpy as np
import librosa
import matplotlib.pyplot as plt
import librosa.display
signal,sample_rate = librosa.load('[email protected]')
spec = librosa.stft(signal,n_fft=512,hop_length=None,win_length = None, window='hann',center = True, pad_mode = 'reflect')
# plot the original signal
plt.figure()
plt.subplot(221)
STFT = librosa.amplitude_to_db(np.abs(spec),ref=np.max)
img = librosa.display.specshow(STFT,sr = sample_rate,x_axis = 'time',y_axis = 'linear')
plt.title('Spectrogram')
plt.subplot(222)
plt.title('Time domain')
time = np.arange(0,len(signal))*(1.0/sample_rate)
plt.plot(time,signal)
plt.xlabel('time/s')
plt.ylabel("amplitude")
plt.show()
二、增加噪声 (Noise addition) (时域)
这里考虑增加的噪声均为均值为0,标准差为1的高斯白噪声,那么我们有两种方法对数据进行加噪。
①、控制噪声因子
def add_noise1(x, w= 0.005):
# w: the noise coefficient
output = x + w*np.random.normal(loc = 0,scale = 1,size=len(x))
return output
# plot the editted signal
plt.subplot(223)
enhanced_STFT = librosa.amplitude_to_db(np.abs(enhanced_spec),ref=np.max)
enhanced_img = librosa.display.specshow(enhanced_STFT,sr = sample_rate,x_axis = 'time',y_axis = 'linear')
plt.title('Spectrogram (add noise)')
plt.subplot(224)
plt.title('Time domain (add noise)')
time = np.arange(0,len(signal))*(1.0/sample_rate)
plt.plot(time,signal)
plt.xlabel('time/s')
plt.ylabel("amplitude")
plt.show()
②、控制信噪比
可以根据信噪比公式来推导噪声并控制噪声。 此处我们设定SNR= 20[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ChcahsS0-1677763237295)(D:\Majority\算法\typora\image-20230301105101995.png)]
def add_noise2(x,snr):
"""
:param x: The clean speech signal
:param snr: The signal/noise ratio
:return: The noisy speech signal with specific snr
"""
P_signal = np.mean(x**2) # the power of signal
k = np.sqrt(P_signal/10 ** (snr/10.0))
return x + np.random.randn(len(x))*k
三、混响增强 (Reverberation addition) (时域)
这里主要使用Image Source Method(镜像源方法) 来实现语音加混响,有两种方法实现,第一种是直接调用python库 ---------- P y r o o m a c o u s t i c s Pyroomacoustics Pyroomacoustics 来实现音频加混响,第二种是按照理论推导一步步实现音频加混响,可以通过第一种方法直接实现。
方法一:Pyroomacoustic 库实现音频加混响
- 1、创建房间 (定义房间大小,所需混响时间,墙面材料,允许的最大反射次数)
- 2、在房间内创建信号源
- 3、在房间内放置麦克风
- 4、创建房间冲激响应
- 5、模拟声音传播
调用Pyroomacoustic 库代码如下:
# This script is used to add reverberation in the room
import numpy as np
import pyroomacoustics as pra
import matplotlib.pyplot as plt
import librosa
import librosa.display
# 1、create the room
# define the required reverberant time and the size of room
rt60_tgt = 0.5 # required reverberant time, s
room_dim = [9, 7.5, 3.5] # define a 9m x 7.5m x 3.5m 's room
# use sabine's formula to calculate the energy absorbed by the wall and then maximum reflected number
e_absorption, max_order = pra.inverse_sabine(rt60_tgt,room_dim) # return the energy absorbed by wall and the maximum reflected times
# by the way, we can define the wall's material and the maximum reflected order
# m = pra.Material(energy_absorption = "hard_surface") # define different wall's material
# max_order = 3
# simulate the room
room = pra.ShoeBox(room_dim,fs=16000,materials=pra.Material(e_absorption),max_order=max_order)
# 2、create a source located at [2.5,3.73,1.76], radiated from 0.3s
audio,_ = librosa.load('[email protected]',sr = 16000)
room.add_source([2.5,3.73,1.76],signal = audio,delay=0.3)
# 3、put the microphones in the room
# define the positions of the microphone:(ndim, nmics) Each columns includes one coordinate of microphone
# here we create an array with two microphones which locate at [6.3, 4.87, 1.2] and [6.3, 4.93, 1.2] respectively
mic_locs = np.c_[
[6.3,4.87,1.2], # mic1
[6.3,4.93,1.2], # mic2
]
# put the microphone into the room
room.add_microphone_array(mic_locs) # put the microphone in the room
# 4、create the room impulse response
room.compute_rir()
# 5、simulate the propogation of the sound, and the signal from each source will convolve with corresponding rir, and the output
# will be summared based on microphone
room.simulate()
# store all the signal to 'wav' file
room.mic_array.to_wav('./16kreverb_ISM.wav',norm = True,bitdepth = np.float32,)
# measure the reverberant time
rt60 = room.measure_rt60()
print('The desired RT60 was {}'.format(rt60_tgt))
print('The measured RT60 is {}'.format(rt60[1,0]))
plt.figure()
# plot the RIR
rir_1_0 = room.rir[1][0] # the RIR between mic 1 and source 0
rir_2_0 = room.rir[0][0] # the RIR between mic 0 and source 0
plt.subplot(221)
plt.plot(np.arange(len(rir_1_0))/room.fs,rir_1_0)
plt.title('The RIR from source 0 to mic 1')
plt.xlabel('time [s]')
plt.subplot(222)
plt.plot(np.arange(len(rir_2_0))/room.fs,rir_2_0)
plt.title('The RIR from source 0 to mic 2')
plt.xlabel('time[s]')
# plt the signal receiving by microphone1 and microphone 0
plt.subplot(223)
plt.plot(np.arange(len(room.mic_array.signals[1,:]))/room.fs, room.mic_array.signals[1,:])
plt.title('Microphone 1 signal')
plt.xlabel('Time [s]')
plt.subplot(224)
plt.plot(np.arange(len(room.mic_array.signals[0,:]))/room.fs, room.mic_array.signals[0,:])
plt.title('Microphone 0 signal')
plt.xlabel('Time [s]')
#
plt.tight_layout()
# plot the original spectrogram
spec_original = librosa.stft(audio,n_fft = 512,hop_length = None, win_length = None, window='hann',center = True, pad_mode = 'reflect')
stft_original = librosa.amplitude_to_db(np.abs(spec_original),ref=np.max)
plt.figure()
plt.subplot(321)
img1 = librosa.display.specshow(stft_original,sr=16000,x_axis = 'time',y_axis = 'linear')
plt.title('Spectrogram of clean signal')
plt.subplot(322)
plt.plot(np.arange(len(audio))/16000,audio)
plt.title('clean signal')
plt.xlabel('Time [s]')
plt.ylabel('Amplitude')
# plot the processed spectrogram (mic 0)
spec_mic0 = librosa.stft(room.mic_array.signals[0,:],n_fft = 512,hop_length = None, win_length = None, window='hann',center = True, pad_mode = 'reflect')
stft_mic0 = librosa.amplitude_to_db(np.abs(spec_mic0),ref=np.max)
plt.subplot(323)
img1 = librosa.display.specshow(stft_mic0,sr=16000,x_axis = 'time',y_axis = 'linear')
plt.title('Spectrogram of mic 0')
plt.subplot(324)
plt.plot(np.arange(len(room.mic_array.signals[0,:]))/room.fs, room.mic_array.signals[0,:])
plt.title('Microphone 0 signal')
plt.xlabel('Time [s]')
# plot the processed spectrogram (mic 1)
spec_mic1 = librosa.stft(room.mic_array.signals[1,:],n_fft = 512,hop_length = None, win_length = None, window='hann',center = True, pad_mode = 'reflect')
stft_mic1 = librosa.amplitude_to_db(np.abs(spec_mic1),ref=np.max)
plt.subplot(325)
img1 = librosa.display.specshow(stft_mic1,sr=16000,x_axis = 'time',y_axis = 'linear')
plt.title('Spectrogram of mic 1')
plt.subplot(326)
plt.plot(np.arange(len(room.mic_array.signals[1,:]))/room.fs, room.mic_array.signals[1,:])
plt.title('Microphone 1 signal')
plt.xlabel('Time [s]')
plt.tight_layout()
plt.show()
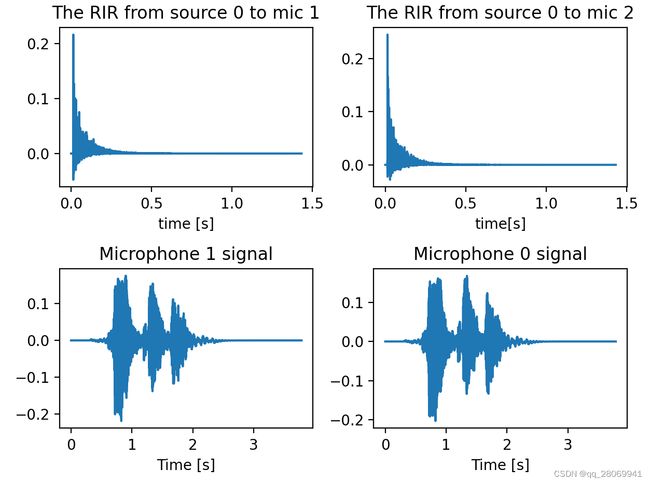
可以分别看到到达mic0和mic1的房间的RIR以及分别此时mic0和mic1采集到的音频数据信号。
再分别画出干净信号,mic0和mic1对应的spectrogram如下图所示:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FrdPvyUa-1677763237297)(D:\Majority\算法\typora\image-20230301163646304.png)]
可以从spectrogram中看到明显加了混响后的信号多了一些能量拖尾,并且如果收听增加了混响后的语音,可以很明显感觉到混响的增加。
方法二:Image Source Method 算法
镜像源法的算法原理为:
我们考虑每个反射面都是一个镜像,也就是说,如果我们在开放空间内有一面平整墙面,那么此时一个声源就可以等价视作为两个声源。如果开放空间中有两面垂直的平整墙面,那么一个声源就可以等效为4个,三面就是八个…进而拓展到封闭的三维空间中,也就是六个面。关于这一块的详细代码可以看:语音数据增强及python实现 - 凌逆战 - 博客园 (cnblogs.com) 以及 audiolabs/rir-generator (github.com)
四、波形位移 (time shifting) (时域)
语音波形在时域的位移我们可以用 n u m p y . r o l l numpy.roll numpy.roll 函数将整个数据向右移动shift的距离
numpy.roll(a,shift,axis = None)
这里的参数:
- a : 数组 a:数组 a:数组
- s h i f t : 滚动的长度 shift: 滚动的长度 shift:滚动的长度
- a x i s : 滚动的维度 axis: 滚动的维度 axis:滚动的维度, 0 为垂直滚动,1为水平滚动,如果设置为None,会将数组扁平化,进行滚动操作后再恢复原始形状
比如:
x = np.arange(10)
# array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
print(np.roll(x, 2))
# array([8, 9, 0, 1, 2, 3, 4, 5, 6, 7])
def time_shift(x, shift):
# shift:移动的长度
return np.roll(x, int(shift))
Augmentation = time_shift(wav_data, shift=fs//2)
此时我们向右移动了 f s / 2 = 8000 fs/2 = 8000 fs/2=8000个采样点。
# This script is used to shift the signal
import numpy as np
import librosa
import librosa.display
import matplotlib.pyplot as plt
def time_shift(x,shift):
# shift: The length of shifting
return np.roll(x, int(shift))
signal,_ = librosa.load('[email protected]')
spec_clean = librosa.stft(signal,n_fft = 512,hop_length = None,win_length = None, window ='hann', center = True, pad_mode = 'reflect')
stft_clean = librosa.amplitude_to_db(np.abs(spec_clean),ref = np.max)
plt.figure()
plt.subplot(221)
librosa.display.specshow(stft_clean,sr = 16000,x_axis = 'time',y_axis = 'linear')
plt.title('Spectrogram of clean signal')
plt.subplot(222)
plt.plot(np.arange(len(signal))/16000,signal)
plt.title('clean signal')
plt.xlabel('Time[s]')
plt.ylabel('Amplitude')
# plot the shifted signal
shifted_signal = time_shift(signal,16000/2)
spec_shifted = librosa.stft(shifted_signal,n_fft = 512,hop_length = None,win_length = None, window ='hann', center = True, pad_mode = 'reflect')
stft_shifted = librosa.amplitude_to_db(np.abs(spec_shifted),ref = np.max)
plt.subplot(223)
librosa.display.specshow(stft_shifted,sr = 16000,x_axis = 'time',y_axis = 'linear')
plt.title('Spectrogram of shifted signal')
plt.subplot(224)
plt.plot(np.arange(len(shifted_signal))/16000,shifted_signal)
plt.title('shifted signal')
plt.xlabel('Time[s]')
plt.ylabel('Amplitude')
plt.tight_layout()
plt.show()
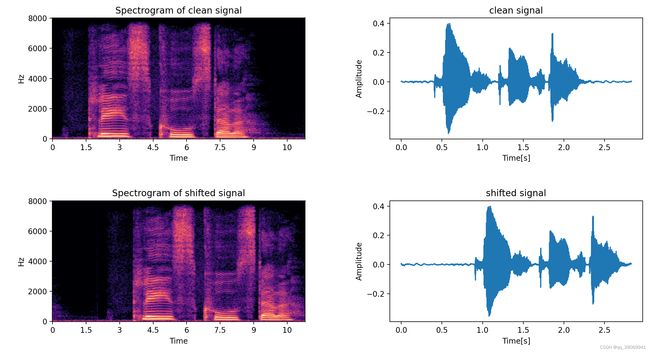
五、音高(音调)增强 (Pitch shifting) (频域)
在这里我们在频率轴上缩放频谱图,从而改变音高,音高修正只会改变音高但是不会影响音速,一般在将步数取在-5和5之间。下图为上移大三度。
代码如下:
# This script is used to shift the pitch
import numpy as np
import librosa
import librosa.display
import matplotlib.pyplot as plt
def pitch_shifting(x,sr,n_steps,bins_peroctave=12):
'''
:param x: input signal
:param sr: sample rate
:param n_steps: how many steps should it move
:param bins_peroctave: how many steps per octave
:return: the result of pitch shifting
'''
enhancement = librosa.effects.pitch_shift(x,sr,n_steps,bins_per_octave = bins_peroctave)
return enhancement
signal,_ = librosa.load('[email protected]')
spec_clean = librosa.stft(signal,n_fft = 512,hop_length = None,win_length = None, window ='hann', center = True, pad_mode = 'reflect')
stft_clean = librosa.amplitude_to_db(np.abs(spec_clean),ref = np.max)
plt.figure()
plt.subplot(221)
librosa.display.specshow(stft_clean,sr = 16000,x_axis = 'time',y_axis = 'linear')
plt.title('Spectrogram of clean signal')
plt.subplot(222)
plt.plot(np.arange(len(signal))/16000,signal)
plt.title('clean signal')
plt.xlabel('Time[s]')
plt.ylabel('Amplitude')
# plot the shifted signal
shifted_signal = pitch_shifting(signal,16000,n_steps = 4, bins_peroctave=12) # Move up three degrees
spec_shifted = librosa.stft(shifted_signal,n_fft = 512,hop_length = None,win_length = None, window ='hann', center = True, pad_mode = 'reflect')
stft_shifted = librosa.amplitude_to_db(np.abs(spec_shifted),ref = np.max)
plt.subplot(223)
librosa.display.specshow(stft_shifted,sr = 16000,x_axis = 'time',y_axis = 'linear')
plt.title('Spectrogram of shifted signal')
plt.subplot(224)
plt.plot(np.arange(len(shifted_signal))/16000,shifted_signal)
plt.title('shifted signal')
plt.xlabel('Time[s]')
plt.ylabel('Amplitude')
plt.tight_layout()
plt.show()
响音速,一般在将步数取在-5和5之间。下图为上移大三度。
[外链图片转存中…(img-StFuADK5-1677763237297)]
代码如下:
# This script is used to shift the pitch
import numpy as np
import librosa
import librosa.display
import matplotlib.pyplot as plt
def pitch_shifting(x,sr,n_steps,bins_peroctave=12):
'''
:param x: input signal
:param sr: sample rate
:param n_steps: how many steps should it move
:param bins_peroctave: how many steps per octave
:return: the result of pitch shifting
'''
enhancement = librosa.effects.pitch_shift(x,sr,n_steps,bins_per_octave = bins_peroctave)
return enhancement
signal,_ = librosa.load('[email protected]')
spec_clean = librosa.stft(signal,n_fft = 512,hop_length = None,win_length = None, window ='hann', center = True, pad_mode = 'reflect')
stft_clean = librosa.amplitude_to_db(np.abs(spec_clean),ref = np.max)
plt.figure()
plt.subplot(221)
librosa.display.specshow(stft_clean,sr = 16000,x_axis = 'time',y_axis = 'linear')
plt.title('Spectrogram of clean signal')
plt.subplot(222)
plt.plot(np.arange(len(signal))/16000,signal)
plt.title('clean signal')
plt.xlabel('Time[s]')
plt.ylabel('Amplitude')
# plot the shifted signal
shifted_signal = pitch_shifting(signal,16000,n_steps = 4, bins_peroctave=12) # Move up three degrees
spec_shifted = librosa.stft(shifted_signal,n_fft = 512,hop_length = None,win_length = None, window ='hann', center = True, pad_mode = 'reflect')
stft_shifted = librosa.amplitude_to_db(np.abs(spec_shifted),ref = np.max)
plt.subplot(223)
librosa.display.specshow(stft_shifted,sr = 16000,x_axis = 'time',y_axis = 'linear')
plt.title('Spectrogram of shifted signal')
plt.subplot(224)
plt.plot(np.arange(len(shifted_signal))/16000,shifted_signal)
plt.title('shifted signal')
plt.xlabel('Time[s]')
plt.ylabel('Amplitude')
plt.tight_layout()
plt.show()