数字信号处理及python实现(三)
数字信号处理及python实现三
- 抽样引起的混叠
- 抽样的频域视图
- 样本重建信号
-
- 拟合正弦波
- 线性与多项式内插
- 理想低通滤波器
这是参考知乎的数字信号处理及matlab实现的python实现版本,参考连接
上一期:数字信号处理及python实现(二)
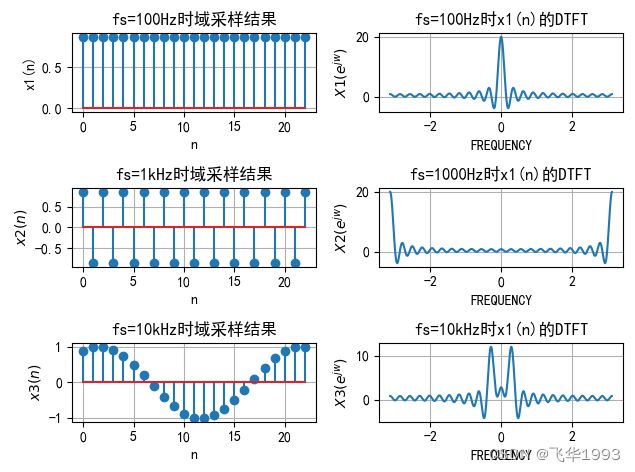
抽样引起的混叠
def test_sample1(self):
signal = Signal()
f0 = 500
n = np.array(list(range(0, 23)))
fs1 = 100 # 采样频率为100Hz
x1 = np.sin(2 * np.pi * f0 * n / fs1 + np.pi / 3)
X1, W1 = signal.dtft(x1, 1000) # 对x1进行DTFT变换
fs2 = 1000 # 采样频率为1kHz
x2 = np.sin(2 * np.pi * f0 * n / fs2 + np.pi / 3)
X2, W2 = signal.dtft(x2, 1000) # 对x2进行DTFT变换
fs3 = 10000 # 采样频率为10kHz
x3 = np.sin(2 * np.pi * f0 * n / fs3 + np.pi / 3)
X3, W3 = signal.dtft(x3, 1000) # 对x3进行DTFT变换
plt.subplot(3, 2, 1);
plt.stem(n, x1) # 绘制fs = 100
# Hz时域采样结果
plt.title('fs=100Hz时域采样结果')
plt.xlabel('n')
plt.ylabel('x1(n)')
plt.grid(visible=True)
plt.subplot(3, 2, 2)
plt.plot(W1, X1)
plt.title('fs=100Hz时x1(n)的DTFT')
plt.xlabel('FREQUENCY')
plt.ylabel('$X1(e^{jw})$')
plt.grid(visible=True)
plt.subplot(3, 2, 3)
plt.stem(n, x2) # 绘制fs = 1
# kHz时域采样结果
plt.title('fs=1kHz时域采样结果')
plt.xlabel('n')
plt.ylabel('$x2(n)$')
plt.grid(visible=True)
plt.subplot(3, 2, 4)
plt.plot(W2, X2)
plt.title('fs=1000Hz时x1(n)的DTFT')
plt.xlabel('FREQUENCY')
plt.ylabel('$X2(e^{jw})$')
plt.grid(visible=True)
plt.subplot(3, 2, 5);
plt.stem(n, x3) # 绘制fs = 10
# kHz时域采样结果
plt.title('fs=10kHz时域采样结果')
plt.xlabel('n')
plt.ylabel('$x3(n)$')
plt.grid(visible=True)
plt.subplot(3, 2, 6)
plt.plot(W3, X3)
plt.title('fs=10kHz时x1(n)的DTFT')
plt.xlabel('FREQUENCY')
plt.ylabel('$X3(e^{jw})$')
plt.grid(visible=True)
plt.tight_layout()
plt.savefig('data/images/sample1.png')
抽样的频域视图
def test_sample_fourier(self):
dt = 0.00001 # 给出一个无限小的间隔
t = np.arange(-0.005, 0.005 + dt, dt) # 给出t的取值范围
xa = np.exp(-1000 * abs(t)) # xa的时域表达式
Wmax = 2 * np.pi * 2000 # 给出频率的最大值
K = 600
k = np.array(list(range(0, K + 1)))
W = k * Wmax / K # W的范围
Xa = np.array(np.matrix(xa) * np.exp(np.complex(0, -1) * np.matrix(t).T * np.matrix(W)) * dt)
Xa = np.real(Xa) # 连续时间傅里叶变换
len_W = len(W)
W.resize(1, len_W)
W = np.concatenate([-np.fliplr(W)[0], W[0][1:]], axis=0) # 给出频率的范围
Xa = np.concatenate([np.fliplr(Xa)[0], Xa[0][1:]], axis=0) # 给出Xa的范围
plt.subplot(1, 2, 1)
plt.plot(t * 1000, xa) # 绘出xa(t)的时域图形
plt.title('xa(t)的时域图形')
plt.xlabel('t')
plt.ylabel('xa(t)')
plt.subplot(1, 2, 2)
plt.plot(W / (2 * np.pi * 1000), Xa * 1000) # 绘出xa(t)的傅里叶变换的频谱
plt.title('xa(t)的傅里叶变换')
plt.xlabel('FREQUENCY')
plt.ylabel('$Xa(jw)$')
plt.tight_layout()
plt.savefig('data/images/sample_fourier.png')
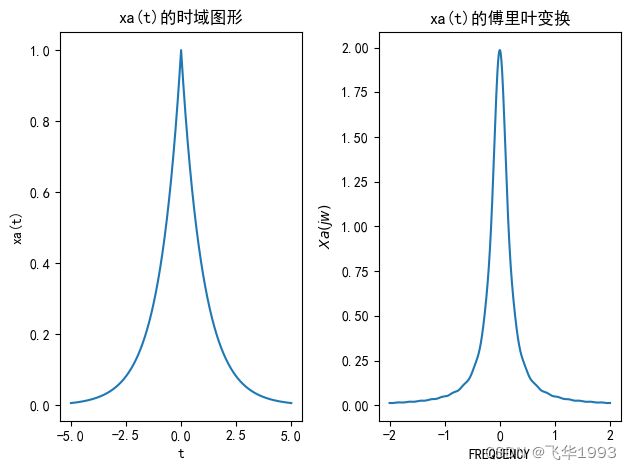
e.g. x a ( t ) = e − 1000 ∣ t ∣ x_a(t)=e^{-1000|t|} xa(t)=e−1000∣t∣,绘制其傅里叶变换 X a ( j Ω ) X_a(j\Omega) Xa(jΩ)
def test_sample_fourier(self):
dt = 0.00001 # 给出一个无限小的间隔
t = np.arange(-0.005, 0.005 + dt, dt) # 给出t的取值范围
xa = np.exp(-1000 * abs(t)) # xa的时域表达式
Wmax = 2 * np.pi * 2000 # 给出频率的最大值
K = 600
k = np.array(list(range(0, K + 1)))
W = k * Wmax / K # W的范围
Xa = np.array(np.matrix(xa) * np.exp(np.complex(0, -1) * np.matrix(t).T * np.matrix(W)) * dt)
Xa = np.real(Xa) # 连续时间傅里叶变换
len_W = len(W)
W.resize(1, len_W)
W = np.concatenate([-np.fliplr(W)[0], W[0][1:]], axis=0) # 给出频率的范围
Xa = np.concatenate([np.fliplr(Xa)[0], Xa[0][1:]], axis=0) # 给出Xa的范围
plt.subplot(1, 2, 1)
plt.plot(t * 1000, xa) # 绘出xa(t)的时域图形
plt.title('xa(t)的时域图形')
plt.xlabel('t')
plt.ylabel('xa(t)')
plt.subplot(1, 2, 2)
plt.plot(W / (2 * np.pi * 1000), Xa * 1000) # 绘出xa(t)的傅里叶变换的频谱
plt.title('xa(t)的傅里叶变换')
plt.xlabel('FREQUENCY')
plt.ylabel('$Xa(jw)$')
plt.tight_layout()
plt.savefig('data/images/sample_fourier.png')
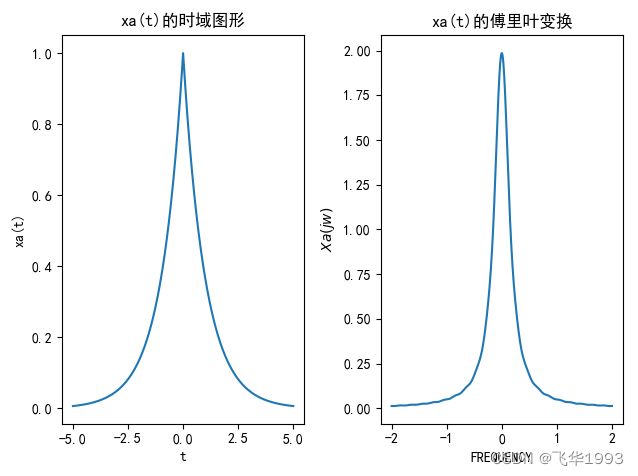
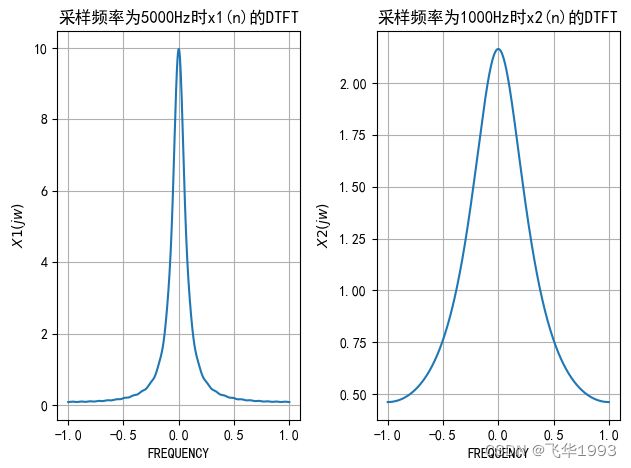
当频率为 5000 H z 5000Hz 5000Hz和 1000 H z 1000Hz 1000Hz分别时,画出其DTFT
def test_sample_fourier_frequency(self):
t1 = 0.0002 # 频率5000Hz进行采样
t2 = 0.001 # 频率1000Hz进行采样
n = np.array(list(range(-25, 26)))
x1 = np.exp(-1000 * abs(n * t1)) # x1的时域表达式
x2 = np.exp(-1000 * abs(n * t2)) # x2的时域表达式
K = 500
k = np.array(list(range(0, K + 1)))
w = k * np.pi / K # w的取值范围
X1 = np.array(np.matrix(x1) * np.exp(np.complex(0, -1) * np.matrix(n).T * np.matrix(w)))
X1 = np.real(X1) # 做x1的DTFTX1
X2 = np.array(np.matrix(x2) * np.exp(np.complex(0, -1) * np.matrix(n).T * np.matrix(w)))
X2 = np.real(X2) # 做x2的DTFTX2
len_w = len(w)
w.resize(1, len_w)
w = np.concatenate([-np.fliplr(w)[0], w[0][1:]], axis=0) # 给出频率的范围
X1 = np.concatenate([np.fliplr(X1)[0], X1[0][1:]], axis=0) # 给出X1的范围
X2 = np.concatenate([np.fliplr(X2)[0], X2[0][1:]], axis=0) # 给出X2的范围
plt.subplot(1, 2, 1)
plt.plot(w / np.pi, X1) # 采样频率为5000Hz时x1(n)的DTFT
plt.title('采样频率为5000Hz时x1(n)的DTFT')
plt.xlabel('FREQUENCY')
plt.ylabel('$X1(jw)$')
plt.grid(visible=True)
plt.subplot(1, 2, 2)
plt.plot(w / np.pi, X2) # 采样频率为1000Hz时x2(n)的DTFT
plt.title('采样频率为1000Hz时x2(n)的DTFT');
plt.xlabel('FREQUENCY')
plt.ylabel('$X2(jw)$')
plt.grid(visible=True)
plt.tight_layout()
plt.savefig('data/images/sample_fourier_frequency.png')
样本重建信号
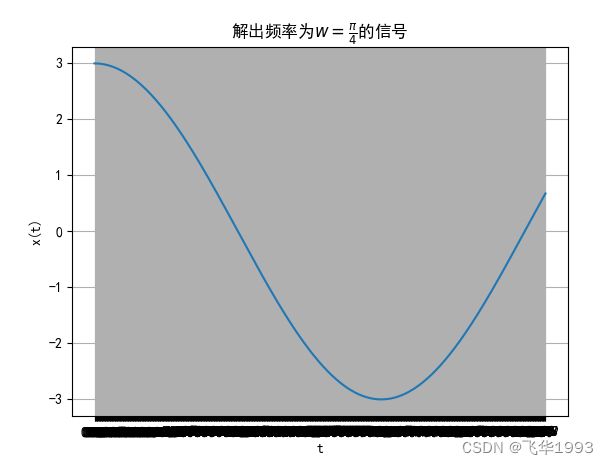
拟合正弦波
def test_reconstruction_fitting(self):
t = np.arange(0, 2 * np.pi + 0.01, 0.01)
x = 3 * np.cos(np.pi * t / 4)
ax = plt.axes()
plt.title('解出频率为w=pi/4的信号')
plt.xlabel('t')
plt.ylabel('x(t)')
ax.set_xticks(t) # 在细密的网格上绘出产生的正弦信号
plt.plot(t, x)
plt.grid(visible=True)
plt.savefig('data/images/sample_reconstruction_fitting.png')
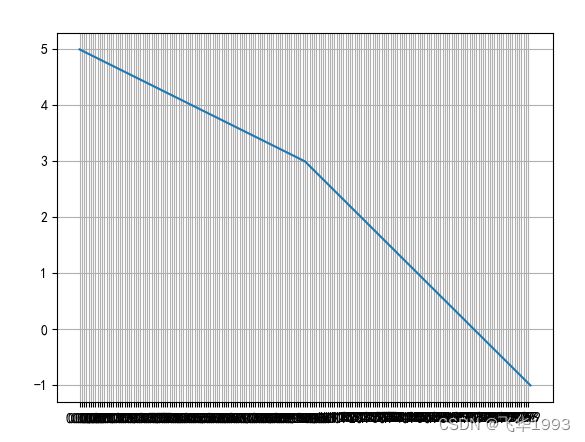
线性与多项式内插
直线段连接样本
def test_interpolation1(self):
x = [5, 3, -1]
n = list(range(0, 3))
t = np.arange(0, 2, 0.01)
ax = plt.axes()
ax.set_xticks(t)
plt.plot(n, x)
plt.grid(visible=True)
plt.savefig('data/images/sample_interpolation1.png')
def test_interpolation2(self):
A = [0.2, 0.4, 0.6, 0.8, 1.0, 0.8, 0.6, 0.4, 0.2]
B = [5, 0, 0, 0, 0, 3, 0, 0, 0, 0, -1]
t = np.array(list(range(-4, 15)))
Z = scipy.signal.convolve(A, B)
vv = [0, 5, 3, -1, 0]
xx = np.array(list(range(-1, 4)))
xq = np.arange(-1, 3 + 0.1, 0.1)
f = scipy.interpolate.interp1d(xx, vv, kind='linear')
vq = f(xq)
plt.subplot(2, 2, 1)
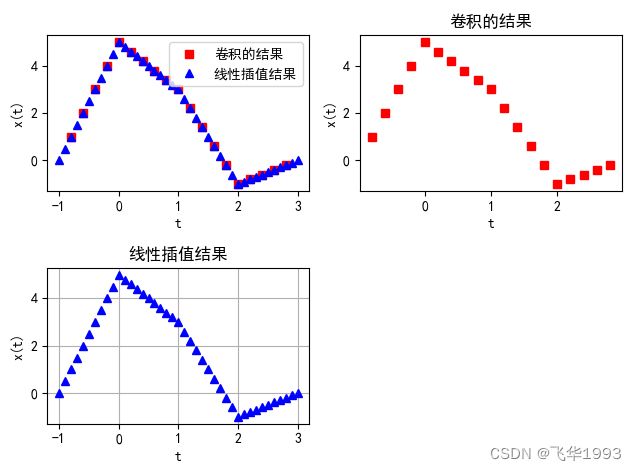
plt.plot(t / 5, Z, 'rs', xq, vq, 'b^')
# 绘出卷积的结果和线性插值的结果,分别用红色和蓝色表示
plt.xlabel('t')
plt.ylabel('x(t)')
plt.legend(['卷积的结果', '线性插值结果'])
plt.subplot(2, 2, 2)
plt.plot(t / 5, Z, 'rs') # 绘出卷积的结果
plt.title('卷积的结果')
plt.xlabel('t')
plt.ylabel('x(t)')
plt.subplot(2, 2, 3)
plt.plot(xq, vq, 'b^') # 线性插值的结果
plt.title('线性插值结果')
plt.xlabel('t')
plt.ylabel('x(t)')
plt.grid(visible=True)
plt.tight_layout()
plt.savefig('data/images/sample_interpolation2.png')
def test_polynomial_interpolation(self):
x = [5, 3, -1]
n = np.array(list(range(0, 3)))
p = np.polyfit(n, x, 2)
nn = np.arange(-5, 5 + 0.5, 0.5)
f = np.polyval(p, nn)
t = np.arange(-5, 5 + 0.1, 0.1)
ax = plt.axes()
plt.legend(['样本点二阶多项式拟合结果'])
plt.xlabel('t')
ax.set_xticks(t)
plt.plot(n, x, 'o', nn, f)
plt.grid(visible=True)
plt.savefig('data/images/polynomial_interpolation.png')
理想低通滤波器
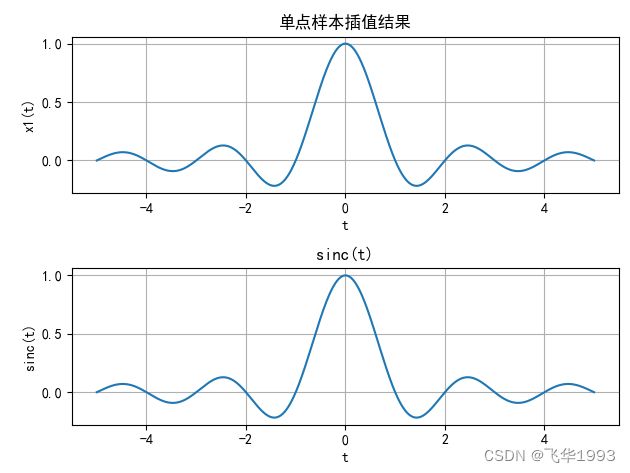
对t=0处的数值为1的单点样本进行插值,绘出大约从-5到5的结果。它应该和sinc函数形状相一致。
def test_low_pass_filter1(self):
t = np.arange(-5, 5 + 0.01, 0.01)
x1 = np.sinc(t)
plt.subplot(2, 1, 1)
plt.plot(t, x1)
plt.title('单点样本插值结果')
plt.xlabel('t')
plt.ylabel('x1(t)')
plt.grid(visible=True)
plt.subplot(2, 1, 2)
plt.plot(t, np.sinc(t))
plt.title('sinc(t)')
plt.xlabel('t')
plt.ylabel('sinc(t)')
plt.grid(visible=True)
plt.tight_layout()
plt.savefig('data/images/low_pass_filter1.png')
对 x a ( t ) Σ n = − ∞ ∞ x a ( n t ) sin ( π ( t − n T s ) / T s ) π ( t − n T s ) / T s x_a(t)\overset{\infty}{\underset{n=-\infty}{\Sigma}}x_a(nt)\frac{\sin(\pi(t-nT_s)/T_s)}{\pi(t-nT_s)/T_s} xa(t)n=−∞Σ∞xa(nt)π(t−nTs)/Tssin(π(t−nTs)/Ts)给定及实验内容中的三点情形进行插值。
def test_low_pass_filter2(self):
xn = np.array([5, 3, -1])
M = 0
N = 2
n = np.array(list(range(M, N + 1)))
Ts = 1
t1 = np.arange(-1, 5 + 0.05, 0.05)
xa = np.matrix(xn) * np.matrix(np.sinc(np.array(
np.matrix(1 / Ts * (np.ones([len(n), 1])) * np.matrix(t1)) - np.array(
np.matrix(n).T * np.matrix(Ts) * np.matrix(np.ones([1, len(t1)]))))))
xa = np.array(xa)[0]
# 基于(3.18)的内插表达式
x = [5, 3, -1] # 直线段的转折点
n = np.array(list(range(0, 3)))
A = [0.2, 0.4, 0.6, 0.8, 1.0, 0.8, 0.6, 0.4, 0.2] # 冲激响应
B = [5, 0, 0, 0, 0, 1, 0, 0, 0, 0, -1]
tt = np.array(list(range(-4, 15)))
C = scipy.signal.convolve(A, B) # 计算线性插值
plt.xlabel('t')
plt.ylabel('x(t)') # 拟合正弦波
plt.plot(t1, xa, n, x, 'o-m', tt / 5, C, '.-b')
# 将直线段与正弦波进行拟合,其中直线拟合用洋红色曲线来表示,线性插值结果用蓝色曲线来表示
plt.stem(range(M, N + 1), xn, 'k')
plt.legend(['sinc函数', '直线拟合', '线性插值结果'])
plt.grid(visible=True)
plt.savefig('data/images/low_pass_filter2.png')