leetcode363 - 矩形区域不超过 K 的最大数值和(前缀和+二分(TreeSet or 辅助数组动归)
leetcode363 - 矩形区域不超过 K 的最大数值和(前缀和+二分(TreeSet or 辅助数组动归)
- 介绍
- 题目
- 理解题目
- 分析题目
-
- 既然是要使用前缀和,那么总是还是要先初始化
- 朴素前缀和
- 前缀和+二分
-
- 利用TreeSet.ceiling()
-
- 对应代码
- 利用辅助数组
-
- 对应代码
- 致谢参考题解:
介绍
我的LeetCode主页,一题一题解
标签:队列、动态规划、二分查找
363. 矩形区域不超过 K 的最大数值和
难度 困难
363. 矩形区域不超过 K 的最大数值和:
https://leetcode-cn.com/problems/max-sum-of-rectangle-no-larger-than-k
题目
给你一个 m x n 的矩阵 matrix 和一个整数 k ,找出并返回矩阵内部矩形区域的不超过 k 的最大数值和。
题目数据保证总会存在一个数值和不超过 k 的矩形区域。
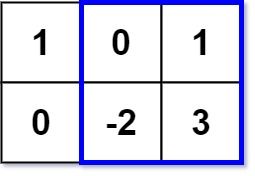
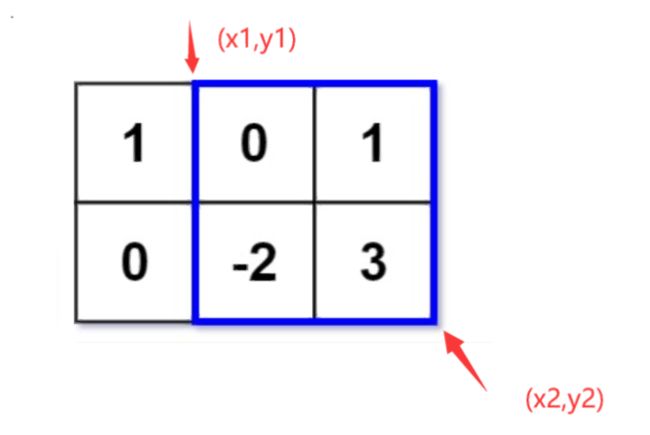
输入:matrix = [[1,0,1],[0,-2,3]], k = 2
输出:2
解释:蓝色边框圈出来的矩形区域 [[0, 1], [-2, 3]] 的数值和是 2,且 2 是不超过 k 的最大数字(k = 2)。
示例 2:
输入:matrix = [[2,2,-1]], k = 3
输出:3
提示:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 100
- -100 <= matrix[i][j] <= 100
- -105 <= k <= 105
进阶:如果行数远大于列数,该如何设计解决方案?
理解题目
题目给出了一个矩阵与一个整数k
其中需要我们一个子矩阵,这个子矩阵满足:
- 其中元素之和小于K
- 不仅要小于k,还要是所有满足条件一中元素和最大的矩阵
分析题目
通过分析题目可以看出这个题可以使用到前缀和来求解
为什么会这么想呢,因为之前做过 304. 二维区域和检索 - 矩阵不可变(我的题解)
同样也是矩形求面积,这样的话可以通过前缀和减少运算的时间
使用暴力遍历的话甚至可以直接使用304题的代码进行运算
既然是要使用前缀和,那么总是还是要先初始化
也就是算出(x1,y1) 为 (0,0) 时的每个子矩阵的元素和
int[][] sum = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
sum[i][j] = sum[i - 1][j] + sum[i][j - 1]
- sum[i - 1][j - 1] + mat[i - 1][j - 1];
}
}
朴素前缀和
直接使用4重循环遍历每一个子矩阵,时间复杂度为O( m^2 * n^2),但是大概是会超时的,所以只意思意思
// 指向子矩阵x1
for (int i = 1; i <= m; i++) {
// 指向子矩阵的y1
for (int j = 1; j <= n; j++) {
// 指向子矩阵的x2
for (int p = i; p <= m; p++) {
// 指向子矩阵的y2
for (int q = j; q <= n; q++) {
// 四重循环遍历子矩阵
}
}
}
}
前缀和+二分
利用TreeSet.ceiling()
子矩阵对应着四条边,那么当我们固定其中3条的时候,最后一条是否能够使用更简答的方式来获得呢?
其中最主要的问题是存在权值为负数的元素,这样就使得数组有序性遭到破坏,使用二分就显得不是很合理
那么有没有能够解决的方案呢?
这里直接给出结果,要看推导过程请看 宫水三叶老师的题解
- 使用TreeSet维护遍历到的所有右边界
- 使用ceiling() 方法用来返回大于或等于给定的元素的最小元素
- 如果存在,则进行二分
- 不存在则往后遍历
- 从结论上来说这个方法是先遍历获得右边界,然后在遍历过的边界中寻找能够成为左边界的值
- 优化就优化在于使用TreeSet这种基于红黑树的这种有序集合,使得最后一条边的获取时间为
O(log n)
这里看宫水三叶老师的一张图:
图中的意思是固定上下和右边界,而对左边界进行二分查找
对应代码
该代码为宫水三叶老师的第一版代码,优化版本还请看宫水三叶老师的题解
class Solution {
public int maxSumSubmatrix(int[][] mat, int k) {
int m = mat.length, n = mat[0].length;
// 预处理前缀和
int[][] sum = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + mat[i - 1][j - 1];
}
}
int ans = Integer.MIN_VALUE;
// 遍历子矩阵的上边界
for (int top = 1; top <= m; top++) {
// 遍历子矩阵的下边界
for (int bot = top; bot <= m; bot++) {
// 使用「有序集合」维护所有遍历到的右边界
TreeSet<Integer> ts = new TreeSet<>();
// 给「有序集合」添加一个初始值
ts.add(0);
// 遍历子矩阵的右边界
for (int r = 1; r <= n; r++) {
// 通过前缀和计算 right
int right = sum[bot][r] - sum[top - 1][r];
// 通过二分找 left
Integer left = ts.ceiling(right - k);
if (left != null) {
// left存在,则表示二分有满足条件的左边界,这时候进行结果更新
int cur = right - left;
ans = Math.max(ans, cur);
}
// 将遍历过的 right 加到有序集合
ts.add(right);
}
}
}
return ans;
}
}
利用辅助数组
- 固定左右边界(当然要固定上下边界也是一样的)
- 设立辅助数组
rowSum[],存储两个边界中间的 每一行 的 矩阵元素和
这里借用lzhlyle老师的图
这个时候就应该很清晰了:
rowSum 连续子数组的和 即为对应上下边界的矩形元素和
这个时候的问题就转变为了求 rowSum[]中元素和小于k的最大子数组
-
二重循环进行遍历求解
-
参照 53. 最大子序和中的解法:
public int maxSubArray(int[] nums) { int len = nums.length, max, dp; if (len == 0) return 0; // 要尽量大,就尽量不要负数 dp = max = nums[0]; for (int i = 1; i < len; i++) { // 之前的和都比现在的小了,那还要干嘛 dp = Math.max(dp, dp + nums[i]); // 更新max max = Math.max(max, dp); } return max; }
这个时候再对返回的max与k的关系进行分析:
-
max还是小于k,那么直接更新到最终的结果中:
res = Math.max(max, res); -
max比k大了,那么再次遍历rowSum[],将所有遍历的小于k的结果都更新到res中去
for (int a = 0; a < row; a++) { int currSum = 0; for (int b = a; b < row; b++) { currSum += sum[b]; if (currSum <= k) res = Math.max(currSum, res); } }
对应代码
class Solution {
public int maxSumSubmatrix(int[][] matrix, int k) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0)
return 0;
int row = matrix.length;
int col = matrix[0].length;
int res = Integer.MIN_VALUE;
// 固定左右边界
for (int i = 0; i < col; i++) {// 枚举左边界
int[] sum = new int[row];
for (int j = i; j < col; j++) {// 枚举右边界
// 只针对行进行求和
for (int r = 0; r < row; r++) {
sum[r] += matrix[r][j];
}
int dp = 0;
int max = sum[0];
for (int n : sum) {
// 之前的和都比现在的小了,那还要干嘛
dp = Math.max(n, dp + n);
// 更新max
max = Math.max(dp, max);
// 如果发现最大的已经为k了,直接返回k
if (max == k)
return max;
}
if (max < k) {
res = Math.max(max, res);
}
else {
for (int a = 0; a < row; a++) {
int currSum = 0;
for (int b = a; b < row; b++) {
currSum += sum[b];
if (currSum <= k)
res = Math.max(currSum, res);
}
}
// 如果发现最大的已经为k了,直接返回k
if (res == k) return res;
}
}
}
return res;
}
}
致谢参考题解:
lzhlyle老师的Java,从暴力开始优化,配图配注释
宫水三叶老师的优化枚举的基本思路 & 将二维抽象成一维 & 最大化「二分」效益 & 空间优化