数据结构之双向链表
目录
引言
链表的分类
双向链表的结构
双向链表的实现
定义
创建新节点
初始化
打印
尾插
头插
判断链表是否为空
尾删
头删
查找与修改
指定插入
指定删除
销毁
顺序表和双向链表的优缺点分析
源代码
dlist.h
dlist.c
test.c
引言
数据结构之路在链表章节,前面介绍过单链表,今天我们来介绍最复杂的链表——双向链表(Double Linked List)
链表的分类
虽然有这么多的链表的结构,但是我们实际中 最常用 还是 两种结构 : 单链表 和 双向带头循环链表1. 无头单向非循环链表 :结构简单,一般不会单独用来存数据。实际中更多是作为其他数据结构的 子结构 ,如 哈希桶、图的邻接表 等等。另外这种结构在 笔试面试 中出现很多。2. 带头双向循环链表 :结构最复杂,一般用在单独存储数据。实际中使用的链表数据结构,都是带头双向循环链表。另外这个结构虽然结构复杂,但是使用代码实现以后会发现结构会带来很多优势, 实现 反而 简单 了,后面我们代码实现了就知道了。
前面我们讲的单链表,就是无头单向非循环链表,而现在讲的双向链表,就是带头双向循环链表。
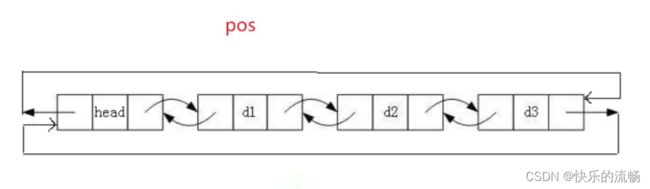
双向链表的结构
注意: 这里的 “带头” 跟前面我们说的“头节点”是两个概念,实际前面的在单链表阶段称呼不严谨,但是为了同学们更好的理解就直接称为单链表的头节点。带头链表里的头节点,实际为“哨兵位” ,哨兵位节点 不存储任何有效元素 ,只是站在这里“放哨的”“哨兵位”存在的意义:遍历循环链表避免死循环
双向链表的实现
定义
与单链表不同,一个节点里有两个指针,分别指向前节点和后节点,实现双向
创建新节点
创建新节点与单链表大致相同,抽离成函数方便创建节点
初始化
双向链表与单链表很大区别,就是在于初始化,创建哨兵位,而哨兵位不存储有效数据,所有这里存入-1,并让prev和next指针都指向自身
打印
首先assert断言,因为phead指向哨兵位,一定不为空,其次因为双向循环链表里没有NULL,所有停止条件就看哨兵位,当cur指针的下一个为哨兵位时,就代表走到尾部了
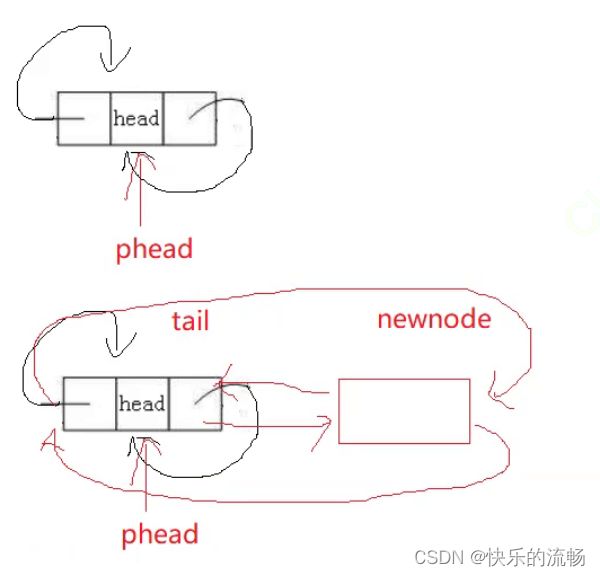
尾插
双向循环结构在空链表插入时,带来了极大的便利。因为prev指针的存在,使得找尾十分方便,不用遍历链表,直接访问哨兵位的上一个节点即可
如果是单链表,是不是还要讨论空链表的特殊情况啊?但是,在双向循环链表中,上述代码就可包含所有情况。因为哨兵位的存在,使得链表一定不为空。
同时,因为哨兵位的存在,我们不用传二级指针了,只用对结构体进行操作。怎么样,有没有发现双向链表的巨大优势?
运行结果
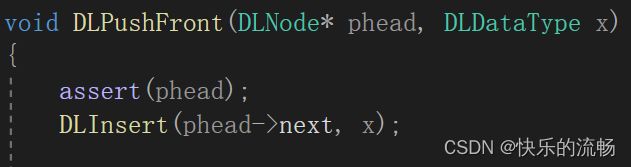
头插
头插时,要注意的就是要先链接后一个节点,再链接前一个节点
运行结果
判断链表是否为空
删除值得注意的是,不能删除哨兵位,要不然后续都无法对链表进行操作,所以专门写个函数来判断除了哨兵位链表是否为空,再用assert断言返回值
如果phead和phead->next相等,则为空,返回1,即为真 ;不相等,则不为空,返回0,即为假
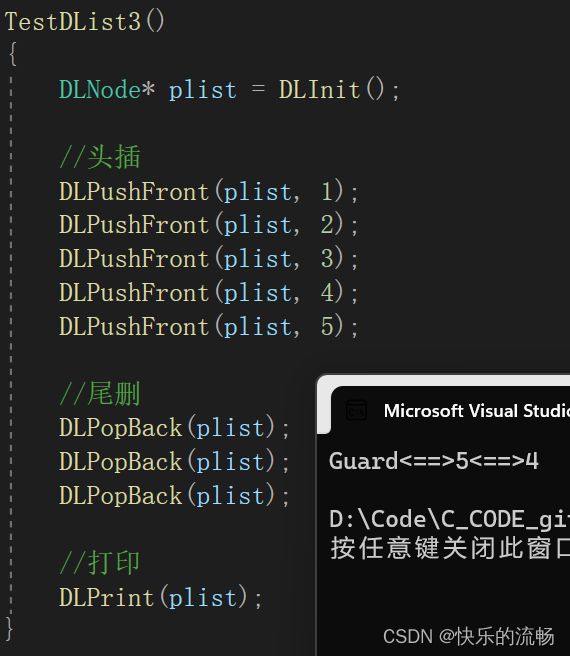
尾删
经历过单链表,双向链表的尾删就显得太简单了。找尾tail直接往phead的上一位,同时创建tailPrev,在释放尾部节点后,双向链接哨兵位
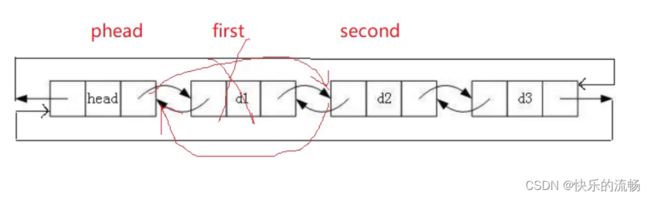
头删
同样,双向链表的头删也很简单。 找头first往phead的下一位,再创建second,在释放头部空间后,双向链接哨兵位
运行结果
查找与修改
双向链表的查找,找到返回地址,找不到返回NULL。要注意的是从哨兵位的下一位开始找,因为哨兵位是不存储有效数据的,直到重新找到哨兵位
运行结果
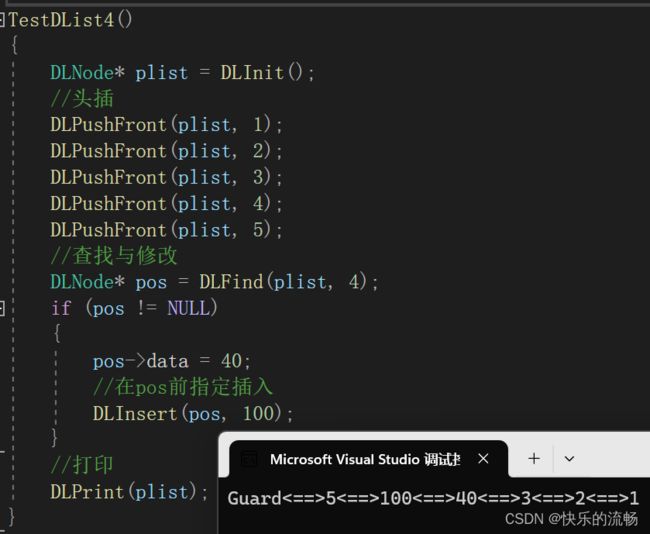
查找到地址后,就可以对其解引用访问,进行修改
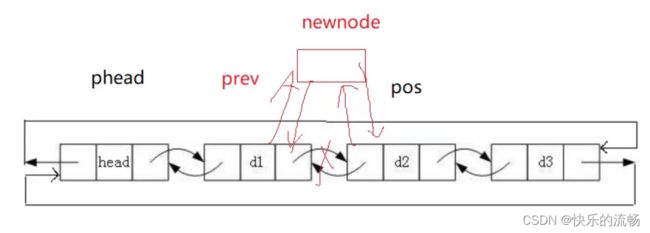
指定插入
在pos前插入
在双向链表,找到pos的上一个节点的地址prev太简单了
运行结果
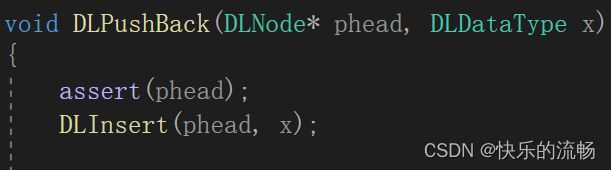
在这里可以复用指定插入函数,快速实现头插和尾插
头插
尾插
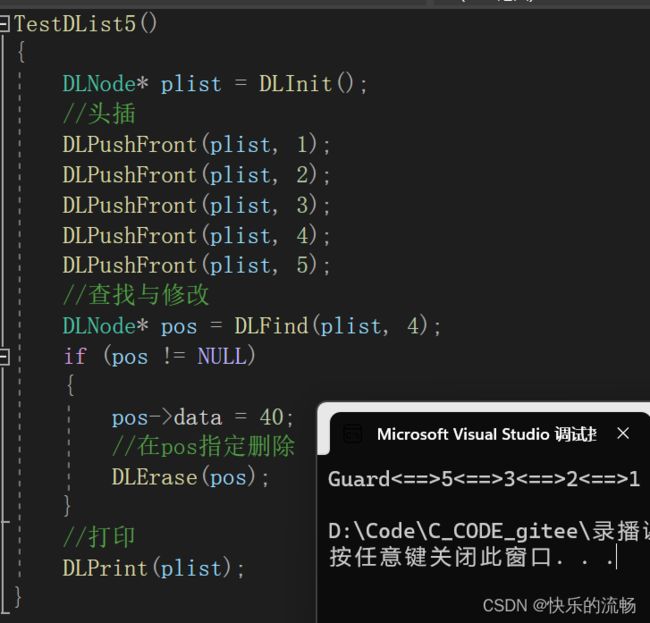
指定删除
创建posPrev和posNext两个指针,释放掉pos的节点空间,再相互链接
在pos删除
运行结果
在这里也可以复用指定删除函数,快速实现头删和尾删
头删
尾删
大家有没有发现,因为双向链表存在哨兵位,链表不为空,省去了很多关于空链表和空指针的讨论,一路下来浑身舒畅
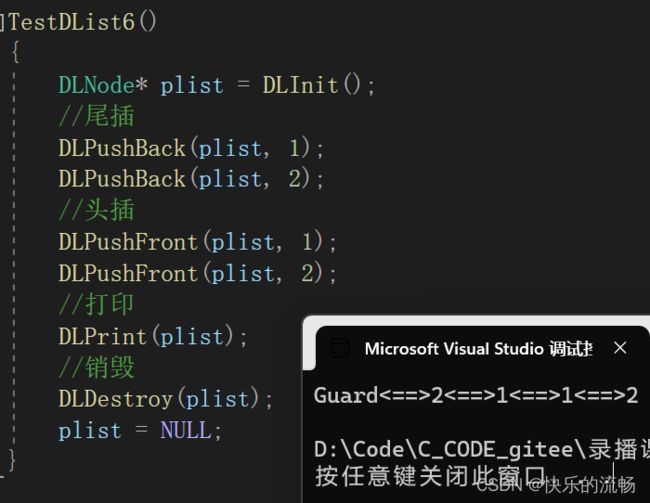
销毁
双向链表的销毁,值得注意的是最后哨兵位也要释放掉,因为为了保持用一级指针的连贯性,所以我们选择最后手动在外部将链表指针置为NULL,实现半自动(和free函数的逻辑一致)
运行结果
这样我们就完成了对双向链表的增删查改等功能的实现
顺序表和双向链表的优缺点分析
我们看到,双向链表的好处是如此巨大的,那是否就代表前面学的顺序表就很low呢?
| 不同点 | 顺序表 | 链表 |
|---|---|---|
| 存储空间上 | 物理上一定连续 | 逻辑上连续,但物理上不一定连续 |
| 随机访问 | 支持O(1) | 不支持:O(N) |
| 任意位置插入或者删除元素 | 可能需要搬移元素,效率低O(N) | 只需修改指针指向 |
| 插入 | 动态顺序表,空间不够时需要扩容 | 没有容量的概念 |
| 应用场景 | 元素高效存储+频繁访问 | 任意位置插入和删除频繁 |
源代码
dlist.h
#pragma once
#include
#include
#include
#include
typedef int DLDataType;
typedef struct DListNode
{
struct DListNode* prev;
struct DListNode* next;
DLDataType data;
}DLNode;
//初始化
DLNode* DLInit();
//打印
void DLPrint(DLNode* phead);
//销毁
void DLDestroy(DLNode* phead);
//检测链表是否为空
bool DLEmpty(DLNode* phead);
//尾插
void DLPushBack(DLNode* phead, DLDataType x);
//尾删
void DLPopBack(DLNode* phead);
//头插
void DLPushFront(DLNode* phead, DLDataType x);
//头删
void DLPopFront(DLNode* phead);
//查找
DLNode* DLFind(DLNode* phead, DLDataType x);
//在pos前指定插入
void DLInsert(DLNode* pos, DLDataType x);
//在pos指定删除
void DLErase(DLNode* pos); dlist.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"dlist.h"
DLNode* BuyDLNode(DLDataType x)
{
DLNode* newnode = (DLNode*)malloc(sizeof(DLNode));
if (newnode == NULL)
{
perror("malloc fail");
return NULL;
}
newnode->data = x;
newnode->prev = NULL;
newnode->next = NULL;
return newnode;
}
DLNode* DLInit()
{
DLNode* phead = BuyDLNode(-1);
phead->next = phead;
phead->prev = phead;
return phead;
}
void DLPrint(DLNode* phead)
{
assert(phead);
DLNode* cur = phead;
printf("Guard");
while (cur->next != phead)
{
cur = cur->next;
printf("<==>%d", cur->data);
}
printf("\n");
}
bool DLEmpty(DLNode* phead)
{
assert(phead);
return phead == phead->next;
}
void DLPushBack(DLNode* phead, DLDataType x)
{
assert(phead);
DLInsert(phead, x);
//DLNode* newnode = BuyDLNode(x);
//DLNode* tail = phead->prev;
//
//tail->next = newnode;
//newnode->prev = tail;
//phead->prev = newnode;
//newnode->next = phead;
}
void DLPopBack(DLNode* phead)
{
assert(phead);
assert(!DLEmpty(phead));
DLErase(phead->prev);
//DLNode* tail = phead->prev;
//DLNode* tailPrev = tail->prev;
//
//free(tail);
//tailPrev->next = phead;
//phead->prev = tailPrev;
}
void DLPushFront(DLNode* phead, DLDataType x)
{
assert(phead);
DLInsert(phead->next, x);
//DLNode* newnode = BuyDLNode(x);
//DLNode* first = phead->next;
//newnode->next = first;
//first->prev = newnode;
//phead->next = newnode;
//newnode->prev = phead;
}
void DLPopFront(DLNode* phead)
{
assert(phead);
assert(!DLEmpty(phead));
DLErase(phead->next);
//DLNode* first = phead->next;
//DLNode* second = first->next;
//second->prev = phead;
//phead->next = second;
//free(first);
}
DLNode* DLFind(DLNode* phead, DLDataType x)
{
assert(phead);
DLNode* cur = phead->next;
while (cur != phead)
{
if (cur->data == x)
{
return cur;
}
cur = cur->next;
}
return NULL;
}
void DLInsert(DLNode* pos, DLDataType x)
{
assert(pos);
DLNode* newnode = BuyDLNode(x);
DLNode* prev = pos->prev;
prev->next = newnode;
newnode->prev = prev;
newnode->next = pos;
pos->prev = newnode;
}
void DLErase(DLNode* pos)
{
assert(pos);
DLNode* posPrev = pos->prev;
DLNode* posNext = pos->next;
posPrev->next = posNext;
posNext->prev = posPrev;
free(pos);
}
void DLDestroy(DLNode* phead)
{
assert(phead);
DLNode* cur = phead->next;
while (cur != phead)
{
DLNode* next = cur->next;
free(cur);
cur = next;
}
free(phead);
}test.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"dlist.h"
TestDList1()
{
DLNode* plist = DLInit();
//尾插
DLPushBack(plist, 1);
DLPushBack(plist, 2);
DLPushBack(plist, 3);
DLPushBack(plist, 4);
DLPushBack(plist, 5);
//头插
DLPushFront(plist, 1);
DLPushFront(plist, 2);
DLPushFront(plist, 3);
DLPushFront(plist, 4);
DLPushFront(plist, 5);
//打印
DLPrint(plist);
}
TestDList2()
{
DLNode* plist = DLInit();
//尾插
DLPushBack(plist, 1);
DLPushBack(plist, 2);
DLPushBack(plist, 3);
DLPushBack(plist, 4);
DLPushBack(plist, 5);
//头删
DLPopFront(plist);
DLPopFront(plist);
DLPopFront(plist);
//打印
DLPrint(plist);
}
TestDList3()
{
DLNode* plist = DLInit();
//头插
DLPushFront(plist, 1);
DLPushFront(plist, 2);
DLPushFront(plist, 3);
DLPushFront(plist, 4);
DLPushFront(plist, 5);
//尾删
DLPopBack(plist);
DLPopBack(plist);
DLPopBack(plist);
//打印
DLPrint(plist);
}
TestDList4()
{
DLNode* plist = DLInit();
//头插
DLPushFront(plist, 1);
DLPushFront(plist, 2);
DLPushFront(plist, 3);
DLPushFront(plist, 4);
DLPushFront(plist, 5);
//查找与修改
DLNode* pos = DLFind(plist, 4);
if (pos != NULL)
{
pos->data = 40;
//在pos前指定插入
DLInsert(pos, 100);
}
//打印
DLPrint(plist);
}
TestDList5()
{
DLNode* plist = DLInit();
//头插
DLPushFront(plist, 1);
DLPushFront(plist, 2);
DLPushFront(plist, 3);
DLPushFront(plist, 4);
DLPushFront(plist, 5);
//查找与修改
DLNode* pos = DLFind(plist, 4);
if (pos != NULL)
{
pos->data = 40;
//在pos指定删除
DLErase(pos);
}
//打印
DLPrint(plist);
}
TestDList6()
{
DLNode* plist = DLInit();
//尾插
DLPushBack(plist, 1);
DLPushBack(plist, 2);
//头插
DLPushFront(plist, 1);
DLPushFront(plist, 2);
//打印
DLPrint(plist);
//销毁
DLDestroy(plist);
plist = NULL;
}
int main()
{
TestDList6();
return 0;
}