优化编辑距离以测量文本相似度
一、说明
编辑距离是一种文本相似度度量,用于测量 2 个单词之间的距离。它有许多方面应用,如文本自动完成和自动更正。
对于这两种用例中的任何一种,系统都会将用户输入的单词与字典中的单词进行比较,以找到最接近的匹配项,然后提出建议。字典可能包含数千个单词,因此应用程序比较 2 个单词的响应可能需要几毫秒。
编辑距离通常是通过准备一个大小矩阵(M+1)x(N+1)(其中 M 和 N 是 2 个单词的长度)并使用 2 个 for 循环遍历所述矩阵,在每次迭代中执行一些计算来计算的。这使得计算一个单词与数千个单词的字典之间的距离非常耗时。
为了加快编辑距离的计算速度,本教程使用向量而不是矩阵进行计算,这样可以节省大量时间。我们将使用 Java 编写此实现的代码。
本教程涵盖的部分如下:
- 为什么使用向量而不是矩阵?
- 使用向量
- Java实现
二、为什么使用向量而不是矩阵?
首先,在使用向量之前,让我们快速总结一下矩阵的距离计算是如何进行的。
对于 2 个单词,例如nice和niace,将创建一个大小矩阵5x6,如下图所示。请注意,蓝色标签不是矩阵的一部分,只是为了清晰起见而添加的。您可以自由决定让给定的单词代表行或列。在此示例中,单词的字符nice代表行。
请注意,矩阵中还有额外的行和列,它们与 2 个单词中的任何字符都不对应。它们放置在那里是为了帮助计算距离。
矩阵的第一行和第一列由从每个字符开始0并递增的值初始化。1例如,第一行的值从 0 到 5。请注意,2 个单词之间的最终距离位于右下角,但要达到它,我们必须计算 2 个单词中所有子集之间的距离。字。
根据初始化的矩阵,将计算 2 个单词的所有子集之间的距离。该过程首先将第一个单词中的第一个子集(仅包含 1 个字符)与第二个单词中的所有子集进行比较。然后将第一个单词的另一个子集(包含 2 个字符)与第二个单词的所有子集进行比较,依此类推。
根据上图中的矩阵,该单词的第一个字符nice是n。它将与第二个单词的所有子集进行比较niace——即使是具有零个字符的子集{_, n, ni, nia, niac, niace}。
让我们看看这两个子集之间的距离是如何计算的。(i,j)对于与 2 个字符A和之间的交集对应的位置处的给定单元格B,我们比较 3 个位置 ( i,j-1)、( i-1,j) 和 ( i-1,j-1) 处的值。如果 2 个字符相同,则位置 ( ) 处的值i,j等于上述 3 个位置中的最小值。否则,它将等于添加 后这 3 个位置处的最小值1。
这里需要注意一点。在计算矩阵第二行中的距离时,位置 ( i-1,j) 和 ( )处的单元格i-1,j-1只是索引。对于矩阵第二列中的距离,位置 ( i,j-1) 和 ( i-1,j-1) 处的单元格也只是索引。
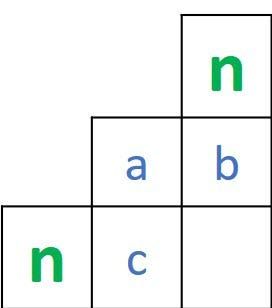
前面的讨论可以表示为 4 个值的矩阵,其中有 3 个已知值和 1 个缺失值,如下图所示。
此类缺失值是通过根据以下方式比较 3 个值来计算的:
dist(X,Y) = min(a, b, c) - if X==Y
dist(X,Y) = min(a, b, c) + 1 - if X!=Y通过应用该方法,下图给出了矩阵第二行中的值。
计算完第二行的距离后,将不再需要第一行的距离。对于第三行距离,我们仅使用第二行中的值,而不是第一行中的值。
换句话说,我们只需要单行已知值来计算一行未知值的距离,不需要整个矩阵。在每行仅使用一次的情况下,使用矩阵计算距离可以保存所有行。
为了解决这个问题,我们根本不会使用矩阵,而是使用向量。
三、使用向量
要使用向量计算距离,第一步是创建该向量。向量长度将等于给定单词的长度+1。nice如果选择第一个单词,则向量长度为4+1=5 。该向量由零初始化,如下所示。
nice该向量中的零将被所选单词中的所有子集与另一个单词中的第一个子集niace(即字符)之间的距离替换n。我们如何计算这样的距离?
当使用矩阵时,需要比较 3 个值,如上一节所述。向量的情况是什么?仅在计算与第二个单词中的第一个子集的距离时,仅需要比较 2 个值。
假设我们正在计算具有索引的元素的距离,i并且距离向量名为distanceVector,那么这 2 个值如下:
- 之前计算的距离:
distanceVector[i-1] - 前一个元素的索引:
i-1
返回的距离是这两个值中的最小值:
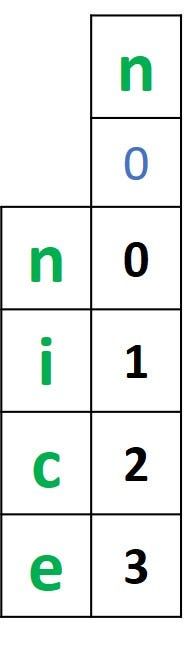
distanceVector[i] = min(distanceVector[i-1], i-1)nice这是计算单词的所有子集与第二个单词的第一个子集之间的距离后的向量niace。
在计算第一个单词的所有子集和第二个单词的第一个子集之间的距离之后,我们可以开始计算第一个单词中的所有子集和第二个单词中的其余子集之间的距离。距离将通过比较以下 3 个值来计算:
- 之前计算的距离:
distanceVector[i-1] - 之前计算的距离:
distanceVector[i] - 与第二个单词进行比较的元素的索引:
j
请注意,i指的是从第一个单词开始的元素索引。
现在我们已经阐明了编辑距离在矩阵和向量中的工作原理,下一节将通过 Java 中的向量实现该距离。
四、Java实现
String除了初始化距离向量之外,要做的第一件事是创建 2 个保存 2 个单词的变量。下面是 Java 中的实现方法:
String token1 = "nice";
String token2 = "niace";
int[] distances = new int[token1.length() + 1]; 向量创建后,默认会初始化为零。下一步是使用for循环计算第一个单词niace 中的所有子集nice与第二个单词中的第一个子集之间的距离。
for (int t1 = 1; t1 <= token1.length(); t1++) {
if (token1.charAt(t1 - 1) == token2.charAt(0)) {
distances[t1] = calcMin(distances[t1 - 1], t1 - 1);
} else {
distances[t1] = calcMin(distances[t1 - 1], t1 - 1) + 1;
}
}
int calcMin(int a, int b, int c) {
if (a <= b && a <= c) {
return a;
} else if (b <= a && b <= c) {
return b;
} else {
return c;
}
}下一步也是最后一步是根据以下代码计算第一个单词中的所有子集与第二个单词中的其余子集之间的距离:
int dist = 0;
for (int t2 = 1; t2 < token2.length(); t2++) {
dist = t2 + 1;
for (int t1 = 1; t1 <= token1.length(); t1++) {
int tempDist;
if (token1.charAt(t1 - 1) == token2.charAt(t2)) {
tempDist = calcMin(dist, distances[t1 - 1], distances[t1]);
} else {
tempDist = calcMin(dist, distances[t1 - 1], distances[t1]) + 1;
}
distances[t1 - 1] = dist;
dist = tempDist;
}
distances[token1.length()] = dist;
}
int calcMin(int a, int b, int c) {
if (a <= b && a <= c) {
return a;
} else if (b <= a && b <= c) {
return b;
} else {
return c;
}
} 两个单词之间的最终距离被保存到变量dist和向量的最后一个元素中distances。
这是一个名为 的完整类LevenshteinDistance,其中名为 的方法levenshtein()保存了计算距离的代码。该方法接受 2 个单词作为参数并返回距离。在该main()方法内部,创建该方法的一个实例来计算 2 个单词nice和之间的距离niace。
前面代码的打印输出是:
The distance is 1这是使用两个不同单词计算距离的另一个示例:
System.out.println("The distance is " + levenshteinDistance.levenshtein("congratulations", "conmgeautlatins"));结果如下:
The distance is 5五 、结论
本教程讨论了仅使用向量来计算编辑距离以返回单词之间的距离。经过优化,仅使用向量,它可以应用于移动设备上运行的应用程序,以便在用户键入搜索或其他文本输入时自动完成和更正单词。