时间序列预测实战(九)PyTorch实现LSTM-ARIMA融合移动平均进行长期预测

一、本文介绍

本文带来的是利用传统时间序列预测模型ARIMA(注意：ARIMA模型不属于机器学习)和利用PyTorch实现深度学习模型LSTM进行融合进行预测，主要思想是->先利用ARIMA先和移动平均结合处理数据的线性部分（例如趋势和季节性），同时利用LSTM捕捉更复杂的非线性模式和长期依赖关系。本文内容包括->讲解LSTM和ARIMA的基本原理、融合的主要思想和依据、模型实战所用数据集介绍 、模型的参数讲解、模型的训练、结果展示、结果分析、以及如何训练你个人数据集。

代码地址->文末有项目的完整代码块分析

适用对象->想要进行长期预测(模型的长期预测功能效果不错)

目录

一、本文介绍 

二、基本原理

三、融合思想

四、数据集

五、训练和预测

1.参数讲解

2.训练

3.预测

3.1结果展示

3.2结果分析

六、如何训练你个人数据集

总结

---

二、基本原理 

其中ARIMA和LSTM的基本原理在我其它的博客中其实以及都分别经过了，大家如果有兴趣可以看我其它博客的讲解其中都有非常仔细的说明，下面简单的给大家介绍一下。 

时间序列预测模型实战案例(六)深入理解ARIMA包括差分和相关性分析

时间序列预测模型实战案例(三)(LSTM)(Python)(深度学习)时间序列预测(包括运行代码以及代码讲解)

1.ARIMA的基本原理

ARIMA（自回归积分滑动平均）模型是一种广泛使用的时间序列分析方法，它的基本原理可以从其名称中的三个部分理解：自回归（AR）、差分（I，即积分的逆过程）、滑动平均（MA）。

• 自回归（AR）部分：

           - 自回归是指一个变量与其过去值的回归关系。
           - 在ARIMA模型中，这表示当前值是过去若干时间点值的线性组合。
           - 这部分模型的目的是捕捉时间序列中的自相关性。

• 差分（I）部分：

           - 差分是为了使非平稳时间序列变得平稳的一种处理方式。
           - 通过对原始数据进行一定次数的差分，可以去除数据中的季节性和趋势性。
           - 差分次数通常根据数据的特性决定。

•  滑动平均（MA）部分：

           - 滑动平均部分是指当前值与过去误差项的线性组合。
           - 这里的误差项是指预测值与实际值之间的差距。
           - MA模型的目的是捕捉时间序列中的随机波动。

在构建ARIMA模型时，需要确定三个主要参数：p（AR项的阶数）、d（差分次数）、q（MA项的阶数）。这些参数共同决定了模型的结构。ARIMA模型通过结合这三个部分，既能处理时间序列的长期趋势和季节性变化，又能捕捉到序列的随机波动，从而在各种场景下进行有效的时间序列预测。

2.LSTM的基本原理

长短期记忆网络（LSTM）是一种特殊类型的递归神经网络（RNN），它专门设计用来处理序列数据的长期依赖问题。LSTM的基本原理主要围绕其独特的内部结构，这种结构使其能够有效地学习和记忆长期信息。下面是LSTM的结构图和几个关键组成部分和它们的作用：

1. 门控制制（Gates）：

   • LSTM通过门（Gates）来控制细胞状态中的信息流。
   • 这些门是一种允许信息通过的方式，它们由一个sigmoid神经网络层和一个逐点乘法操作组成。
   • 门可以学习何时添加或删除信息到细胞状态中，这是通过调节信息流的重要性（权重）来实现的。

• 遗忘门（Forget Gate）：

  • 遗忘门决定了从细胞状态中丢弃什么信息。
  • 它通过查看当前输入和前一隐藏层的输出来决定保留或丢弃每个细胞状态中的信息。

• 输入门（Input Gate）：

  • 输入门用来更新细胞状态。
  • 它首先通过一个sigmoid层决定哪些值将要更新，然后通过一个tanh层创建一个新的候选值向量，这个向量将被添加到状态中。

• 输出门（Output Gate）：

  • 输出门控制着下一个隐藏状态的值。
  • 隐藏状态包含关于先前输入的信息，用于预测或决策。
  • 这个门查看当前的细胞状态，并决定输出的部分。

总结：LSTM通过这种复杂的内部结构，能够有效地解决传统RNN面临的长期依赖问题，。这种网络能够记住长期的信息，同时还可以决定忘记无关紧要或过时的信息。 

3.融合思想

将ARIMA和LSTM结合起来的主要思想是->

结合ARIMA和LSTM的目的是利用ARIMA处理数据的线性部分（例如趋势和季节性），同时利用LSTM捕捉更复杂的非线性模式和长期依赖关系。

这种组合方法可以弥补单一模型的不足。例如，当时间序列数据既包含线性又包含非线性特征时，单独的ARIMA或LSTM可能无法充分捕捉全部信息，而结合使用两者可以提高预测性能。

结合的方式->分阶段预测（先用移动平滑和ARIMA处理，再用LSTM进一步分析）、模型融合（将两个模型的预测结果综合考虑）

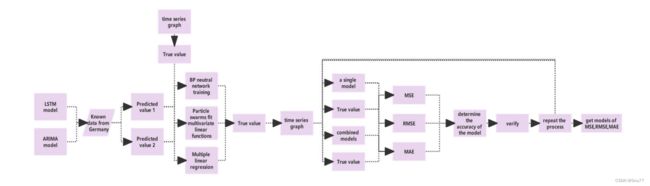
下面的图片是整个结构的网络图，从数据的输出到数据的输出整个过程的描述->

总之，将LSTM和ARIMA结合的核心思想是通过利用两种模型的互补优势，提高对复杂时间序列数据的预测能力。

三、数据集

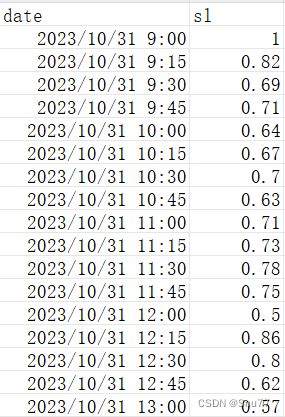
因为本文涉及到ARIMA模型其为单变量的预测模型所以我们的模型有限制必须是单元预测，所以我们的数据集为某公司的业务水平评估数据为从0-1分布，部分截图如下->

四、训练和预测

下面开始分别进行参数的讲解、模型训练、预测、和结果展示和分析。

1.参数讲解

if __name__ == '__main__':
    # Load historical data
    # CSV should have columns: ['date', 'OT']
    strpath= '你数据集的地址CSV格式的文件'
    target = 'OT'  # 预测的列明
    data = pd.read_csv('ETTh1.csv', index_col=0, header=0).tail(1500).reset_index(drop=True)[['target']]

其中的参数讲解我以及在代码中标注出来了应该很好理解，主要修改这两处就可以了。 

2.训练

ARIMA拟合部分->

def get_arima(data, train_len, test_len):
    # prepare train and test data
    data = data.tail(test_len + train_len).reset_index(drop=True)
    train = data.head(train_len).values.tolist()
    test = data.tail(test_len).values.tolist()

    # Initialize model
    model = auto_arima(train, max_p=3, max_q=3, seasonal=False, trace=True,
                       error_action='ignore', suppress_warnings=True, maxiter=10)

    # Determine model parameters
    model.fit(train)
    order = model.get_params()['order']
    print('ARIMA order:', order, '\n')

    # Genereate predictions
    prediction = []
    for i in range(len(test)):
        model = pm.ARIMA(order=order)
        model.fit(train)
        print('working on', i+1, 'of', test_len, '-- ' + str(int(100 * (i + 1) / test_len)) + '% complete')
        prediction.append(model.predict()[0])
        train.append(test[i])

    # Generate error data
    mse = mean_squared_error(test, prediction)
    rmse = mse ** 0.5
    mape = mean_absolute_percentage_error(pd.Series(test), pd.Series(prediction))
    return prediction, mse, rmse, mape

代码讲解->其实这部分没什么好讲的就是首先对数据进行了处理分出了训练集、测试集，然后初始化了一个ARIMA模型(调用了官方的pmdarima库)，然后用fit方法进行自动拟合然后进行结果预测。是一个很标准的ARIMA训练过程如果大家想仔细了解可以看我单独的ARIMA模型讲解里面有具体的分析。 训练过程控制台输出如下->

LSTM训练部分-> 

def get_lstm(data, train_len, test_len, lstm_len=4):
    # prepare train and test data
    data = data.tail(test_len + train_len).reset_index(drop=True)
    dataset = np.reshape(data.values, (len(data), 1))
    scaler = MinMaxScaler(feature_range=(0, 1))
    dataset_scaled = scaler.fit_transform(dataset)
    x_train = []
    y_train = []
    x_test = []

    for i in range(lstm_len, train_len):
        x_train.append(dataset_scaled[i - lstm_len:i, 0])
        y_train.append(dataset_scaled[i, 0])
    for i in range(train_len, len(dataset_scaled)):
        x_test.append(dataset_scaled[i - lstm_len:i, 0])

    x_train = np.array(x_train)
    y_train = np.array(y_train)
    x_train = np.reshape(x_train, (x_train.shape[0], x_train.shape[1], 1))
    x_test = np.array(x_test)
    x_test = np.reshape(x_test, (x_test.shape[0], x_test.shape[1], 1))

    # Convert to PyTorch tensors
    x_train = torch.tensor(x_train).float()
    y_train = torch.tensor(y_train).float()
    x_test = torch.tensor(x_test).float()

    # Create the PyTorch model
    model = LSTMModel(input_dim=1, hidden_dim=lstm_len)
    criterion = torch.nn.MSELoss()
    optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

    total_loss = 0
    # train
    for epoch in range(500):
        model.train()
        optimizer.zero_grad()

        # Forward pass
        y_pred = model(x_train)

        # Compute Loss
        loss = criterion(y_pred.squeeze(), y_train)
        total_loss += loss.item()

        # Backward pass and optimize
        loss.backward()
        optimizer.step()

        # Print training progress
        if (epoch + 1) % 50 == 0:  # 每50轮打印一次
            print(f'Epoch [{epoch + 1}/500], Loss: {loss.item():.4f}')

    # Calculate and print average loss
    average_loss = total_loss / 500
    print(f'Average Loss: {average_loss:.4f}')
    # Prediction
    model.eval()
    predict = model(x_test)
    predict = predict.data.numpy()
    prediction = scaler.inverse_transform(predict).tolist()

    output = []
    for i in range(len(prediction)):
        output.extend(prediction[i])
    prediction = output

    # Error calculation
    mse = mean_squared_error(data.tail(len(prediction)).values, prediction)
    rmse = mse ** 0.5
    mape = mean_absolute_percentage_error(data.tail(len(prediction)).reset_index(drop=True), pd.Series(prediction))

    return prediction, mse, rmse, mape

代码讲解->同样这里最上面是数据处理部分，分解出来训练集和测试集，然后调用了我定义的LSTM模型最后的总代码分析里面有，然后进行训练，最后调用模型进行预测，然后将预测结果和测试集算mse、rmse、和mape 。如果想看LSTM的下详细过程同样可以看我的单模型讲解，训练模型控制台输出如下->

3.预测

进行预测之后控制台会打印预测结果如下->

同时会保存csv文件用于真实值和预测值的对比，如下-> 

3.1结果展示

3.2结果分析

这篇文章的预测结果和我上一篇的SCINet大家有兴趣可以对比一下经过结合ARIMA模型的预测结果明显要好很多，消除了其中一定的数据滞后性，但是还是并没有完全消失，当然可以将ARIMA和更复杂的移动平均方法结合起来没准效果会更好，这里大家可以进行尝试尝试。

五、如何训练你个人数据集

训练你个人数据集需要注意的就是，因为利用ARIMA模型，所以只支持单变量预测，当然也可以替换SARIMA模型进行多元预测这个大家也可以尝试尝试如果有兴趣，把下面的内容填写了就可以用你自己的数据集进行训练了还是比较简单的，没有涉及到复杂的参数类似于Transformer模型那样。

六、完整的代码块分享

import pandas as pd
import numpy as np
from scipy.stats import kurtosis
from pmdarima import auto_arima
import pmdarima as pm
import torch
import torch.nn as nn
from sklearn.metrics import mean_squared_error, mean_absolute_percentage_error
import json
from sklearn.preprocessing import MinMaxScaler


def mean_absolute_percentage_error(actual, prediction):
    actual = pd.Series(actual)
    prediction = pd.Series(prediction)
    return 100 * np.mean(np.abs((actual - prediction))/actual)

def get_arima(data, train_len, test_len):
    # prepare train and test data
    data = data.tail(test_len + train_len).reset_index(drop=True)
    train = data.head(train_len).values.tolist()
    test = data.tail(test_len).values.tolist()

    # Initialize model
    model = auto_arima(train, max_p=3, max_q=3, seasonal=False, trace=True,
                       error_action='ignore', suppress_warnings=True, maxiter=10)

    # Determine model parameters
    model.fit(train)
    order = model.get_params()['order']
    print('ARIMA order:', order, '\n')

    # Genereate predictions
    prediction = []
    for i in range(len(test)):
        model = pm.ARIMA(order=order)
        model.fit(train)
        print('working on', i+1, 'of', test_len, '-- ' + str(int(100 * (i + 1) / test_len)) + '% complete')
        prediction.append(model.predict()[0])
        train.append(test[i])

    # Generate error data
    mse = mean_squared_error(test, prediction)
    rmse = mse ** 0.5
    mape = mean_absolute_percentage_error(pd.Series(test), pd.Series(prediction))
    return prediction, mse, rmse, mape



class LSTMModel(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim=1, num_layers=2):
        super(LSTMModel, self).__init__()
        self.hidden_dim = hidden_dim
        self.num_layers = num_layers

        # Define the LSTM layer
        self.lstm = nn.LSTM(input_dim, hidden_dim, num_layers, batch_first=True)

        # Define the output layer
        self.linear = nn.Linear(hidden_dim, output_dim)

    def forward(self, x):
        # Initialize hidden state with zeros
        h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_dim).requires_grad_()

        # Initialize cell state
        c0 = torch.zeros(self.num_layers, x.size(0), self.hidden_dim).requires_grad_()

        # We need to detach as we are doing truncated backpropagation through time (BPTT)
        # If we don't, we'll backprop all the way to the start even after going through another batch
        out, (hn, cn) = self.lstm(x, (h0.detach(), c0.detach()))

        # Index hidden state of last time step
        out = self.linear(out[:, -1, :])
        return out

def get_lstm(data, train_len, test_len, lstm_len=4):
    # prepare train and test data
    data = data.tail(test_len + train_len).reset_index(drop=True)
    dataset = np.reshape(data.values, (len(data), 1))
    scaler = MinMaxScaler(feature_range=(0, 1))
    dataset_scaled = scaler.fit_transform(dataset)
    x_train = []
    y_train = []
    x_test = []

    for i in range(lstm_len, train_len):
        x_train.append(dataset_scaled[i - lstm_len:i, 0])
        y_train.append(dataset_scaled[i, 0])
    for i in range(train_len, len(dataset_scaled)):
        x_test.append(dataset_scaled[i - lstm_len:i, 0])

    x_train = np.array(x_train)
    y_train = np.array(y_train)
    x_train = np.reshape(x_train, (x_train.shape[0], x_train.shape[1], 1))
    x_test = np.array(x_test)
    x_test = np.reshape(x_test, (x_test.shape[0], x_test.shape[1], 1))

    # Convert to PyTorch tensors
    x_train = torch.tensor(x_train).float()
    y_train = torch.tensor(y_train).float()
    x_test = torch.tensor(x_test).float()

    # Create the PyTorch model
    model = LSTMModel(input_dim=1, hidden_dim=lstm_len)
    criterion = torch.nn.MSELoss()
    optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

    total_loss = 0
    # train
    for epoch in range(500):
        model.train()
        optimizer.zero_grad()

        # Forward pass
        y_pred = model(x_train)

        # Compute Loss
        loss = criterion(y_pred.squeeze(), y_train)
        total_loss += loss.item()

        # Backward pass and optimize
        loss.backward()
        optimizer.step()

        # Print training progress
        if (epoch + 1) % 50 == 0:  # 每50轮打印一次
            print(f'Epoch [{epoch + 1}/500], Loss: {loss.item():.4f}')

    # Calculate and print average loss
    average_loss = total_loss / 500
    print(f'Average Loss: {average_loss:.4f}')
    # Prediction
    model.eval()
    predict = model(x_test)
    predict = predict.data.numpy()
    prediction = scaler.inverse_transform(predict).tolist()

    output = []
    for i in range(len(prediction)):
        output.extend(prediction[i])
    prediction = output

    # Error calculation
    mse = mean_squared_error(data.tail(len(prediction)).values, prediction)
    rmse = mse ** 0.5
    mape = mean_absolute_percentage_error(data.tail(len(prediction)).reset_index(drop=True), pd.Series(prediction))

    return prediction, mse, rmse, mape


def SMA(data, window):
    sma = np.convolve(data[target], np.ones(window), 'same') / window
    return sma

def EMA(data, window):

    alpha = 2 / (window + 1)
    ema = np.zeros_like(data)
    ema[0] = data.iloc[0]  # 设置初始值为序列的第一个值

    for i in range(1, len(data)):
        ema[i] = alpha * data.iloc[i] + (1 - alpha) * ema[i - 1]

    return ema

def WMA(data, window):
    weights = np.arange(1, window + 1)
    wma = np.convolve(data[target], weights/weights.sum(), 'same')
    return wma

# 其他复杂的移动平均技术如 DEMA 可以通过组合上述基础方法实现
# 例如，DEMA 是两个不同窗口大小的 EMA 的组合

if __name__ == '__main__':
    # Load historical data
    # CSV should have columns: ['date', 'OT']
    strpath= '你数据集的地址CSV格式的文件'
    target = 'OT'  # 预测的列明
    data = pd.read_csv('ETTh1.csv', index_col=0, header=0).tail(1500).reset_index(drop=True)[[target]]

    talib_moving_averages = ['SMA'] # 替换你想用的方法

    # 创建一个字典来存储这些函数
    functions = {
        'SMA': SMA,
        # 'EMA': EMA,
        # 'WMA': WMA,
        # 添加其他需要的移动平均函数
    }

    # for ma in talib_moving_averages:
    #     functions[ma] = abstract.Function(ma)

    # Determine kurtosis "K" values for MA period 4-99
    kurtosis_results = {'period': []}
    for i in range(4, 100):
        kurtosis_results['period'].append(i)
        for ma in talib_moving_averages:
            # Run moving average, remove last 252 days (used later for test data set), trim MA result to last 60 days
            ma_output = functions[ma](data[:-252], i)[-60:]
            # Determine kurtosis "K" value
            k = kurtosis(ma_output, fisher=False)

            # add to dictionary
            if ma not in kurtosis_results.keys():
                kurtosis_results[ma] = []
            kurtosis_results[ma].append(k)

    kurtosis_results = pd.DataFrame(kurtosis_results)
    kurtosis_results.to_csv('kurtosis_results.csv')

    # Determine period with K closest to 3 +/-5%
    optimized_period = {}
    for ma in talib_moving_averages:
        difference = np.abs(kurtosis_results[ma] - 3)
        df = pd.DataFrame({'difference': difference, 'period': kurtosis_results['period']})
        df = df.sort_values(by=['difference'], ascending=True).reset_index(drop=True)
        if df.at[0, 'difference'] < 3 * 0.05:
            optimized_period[ma] = df.at[0, 'period']
        else:
            print(ma + ' is not viable, best K greater or less than 3 +/-5%')

    print('\nOptimized periods:', optimized_period)

    simulation = {}
    for ma in optimized_period:
        # Split data into low volatility and high volatility time series
        low_vol = pd.Series(functions[ma](data, optimized_period[ma]))
        high_vol = pd.Series(data[target] - low_vol)

        # Generate ARIMA and LSTM predictions
        print('\nWorking on ' + ma + ' predictions')
        try:
            low_vol_prediction, low_vol_mse, low_vol_rmse, low_vol_mape = get_arima(low_vol, 1000, 252)
        except:
            print('ARIMA error, skipping to next MA type')
            continue

        high_vol_prediction, high_vol_mse, high_vol_rmse, high_vol_mape = get_lstm(high_vol, 1000, 252)

        final_prediction = pd.Series(low_vol_prediction) + pd.Series(high_vol_prediction)
        mse = mean_squared_error(final_prediction.values, data[target].tail(252).values)
        rmse = mse ** 0.5
        mape = mean_absolute_percentage_error(data[target].tail(252).reset_index(drop=True), final_prediction)

        # Generate prediction accuracy
        actual = data[target].tail(252).values
        df = pd.DataFrame({'real': actual,'pre': final_prediction}).to_csv('results.csv',index=False)
        result_1 = []
        result_2 = []
        for i in range(1, len(final_prediction)):
            # Compare prediction to previous close price
            if final_prediction[i] > actual[i-1] and actual[i] > actual[i-1]:
                result_1.append(1)
            elif final_prediction[i] < actual[i-1] and actual[i] < actual[i-1]:
                result_1.append(1)
            else:
                result_1.append(0)

            # Compare prediction to previous prediction
            if final_prediction[i] > final_prediction[i-1] and actual[i] > actual[i-1]:
                result_2.append(1)
            elif final_prediction[i] < final_prediction[i-1] and actual[i] < actual[i-1]:
                result_2.append(1)
            else:
                result_2.append(0)

        accuracy_1 = np.mean(result_1)
        accuracy_2 = np.mean(result_2)

        simulation[ma] = {'low_vol': {'prediction': low_vol_prediction, 'mse': low_vol_mse,
                                      'rmse': low_vol_rmse, 'mape': low_vol_mape},
                          'high_vol': {'prediction': high_vol_prediction, 'mse': high_vol_mse,
                                       'rmse': high_vol_rmse},
                          'final': {'prediction': final_prediction.values.tolist(), 'mse': mse,
                                    'rmse': rmse, 'mape': mape},
                          'accuracy': {'prediction vs close': accuracy_1, 'prediction vs prediction': accuracy_2}}

        # save simulation data here as checkpoint
        with open('simulation_data.json', 'w') as fp:
            json.dump(simulation, fp)

    for ma in simulation.keys():
        print('\n' + ma)
        print('Prediction vs Close:\t\t' + str(round(100*simulation[ma]['accuracy']['prediction vs close'], 2))
              + '% Accuracy')
        print('Prediction vs Prediction:\t' + str(round(100*simulation[ma]['accuracy']['prediction vs prediction'], 2))
              + '% Accuracy')
        print('MSE:\t', simulation[ma]['final']['mse'],
              '\nRMSE:\t', simulation[ma]['final']['rmse'],
              '\nMAPE:\t', simulation[ma]['final']['mape'])

总结

到此本文已经全部讲解完成了，希望能够帮助到大家。在这里也给大家推荐一些我其它的博客的时间序列实战案例讲解，其中有数据分析的讲解就是我前面提到的如何设置参数的分析博客，最后希望大家订阅我的专栏，本专栏均分文章均分98，并且免费阅读。

时间序列预测实战(十一)用SCINet实现滚动预测功能(附代码+数据集+原理介绍）

时间序列预测：深度学习、机器学习、融合模型、创新模型实战案例（附代码+数据集+原理介绍）

时间序列预测模型实战案例(十)(个人创新模型)通过堆叠CNN、GRU、LSTM实现多元预测和单元预测

时间序列预测中的数据分析-＞周期性、相关性、滞后性、趋势性、离群值等特性的分析方法

时间序列预测模型实战案例(八)(Informer)个人数据集、详细参数、代码实战讲解

时间序列预测模型实战案例(七)(TPA-LSTM)结合TPA注意力机制的LSTM实现多元预测

时间序列预测模型实战案例(六)深入理解机器学习ARIMA包括差分和相关性分析

时间序列预测模型实战案例(五)基于双向LSTM横向搭配单向LSTM进行回归问题解决

时间序列预测模型实战案例(四)(Xgboost)(Python)(机器学习)图解机制原理实现时间序列预测和分类(附一键运行代码资源下载和代码讲解)

时间序列预测模型实战案例(三)(LSTM)(Python)(深度学习)时间序列预测(包括运行代码以及代码讲解)

【全网首发】(MTS-Mixers)(Python)(Pytorch)最新由华为发布的时间序列预测模型实战案例(一)(包括代码讲解)实现企业级预测精度包括官方代码BUG修复Transform模型

时间序列预测模型实战案例(二)(Holt-Winter)(Python)结合K-折交叉验证进行时间序列预测实现企业级预测精度(包括运行代码以及代码讲解)

最后希望大家工作顺利学业有成！