数据结构——红黑树
数据结构——红黑树
前言
红黑树是map，set，mutilmap，mutilset容器的底层数据结构，也是一种非常重要的数据结构，它在效率上对AVL又做了进一步的优化，因为AVL结构在插入，或删除时，无法避免大量的旋转操作，导致效率有所损耗，但是红黑树，就在这一点有了更好的优化，但是牺牲了平衡性，所以是不是一个完全平衡的二叉搜索树。
一、红黑树的概念和性质
概念：
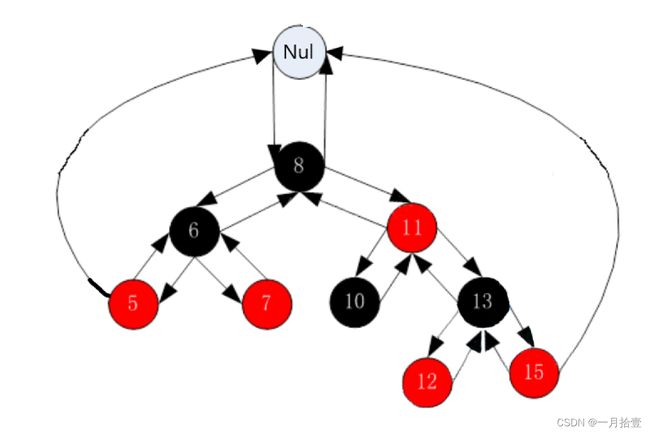
红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。
性质：
1、根节点是黑色的
2、每个节点不是红色的就是黑色的
3、红色节点的子节点一定是黑色的
4、红色节点不能相连
5、从任意节点出发，它每一条路径上的黑色节点数目是相同的
这里有一条总结红黑树的顺口溜：
一头一脚黑，
黑连红不连。
插入看叔伯，
删除看兄弟。
这四句话就概括了红黑树的所有性质，以及插入和删除时应该怎样处理的情况。
二、红黑树节点的定义
#include我们有两个类，一个类是我们的红黑树类，另一个类是叶子节点类
红黑树类：
有两个成员，这里就有红黑树的另一个人为的看法，就是所有空节点，都为黑色节点，根一定是黑色节点，所以在初始化的时候我们不能没有根，初始化时一定要有一个黑色节点作为根节点，那么就有了为什么除了 _root以外还有一个节点作为空节点，所有空节点都指向这个节点。
然后呢，我们为了调整时方便，多使用了一个父指针，指向自己的父节点，因为不用这个的话，未来插入，删除都将变的超级麻烦！后面会有说到。
三、红黑树的旋转
这里我们就不需要再像AVL树一样写四个旋转方法了，因为初学，所以我们需要详细一点，现在我们直接选择同时调用左单旋和右单旋实现双旋转，这样就不需要重复实现了。提高了代码的复用性。
1.右单旋
因为我们在旋转之前就已经完成了颜色的修改，所以我们只需要进行单纯的旋转即可
template<typename Type>
void RBTree<Type>::RotateR(RBTreeNode<Type>*& t, RBTreeNode<Type>* p)
{
RBTreeNode<Type>* s = p->_leftChild;
/*判断即将要旋转的位置是否有左子树，有的话就将其挂在未来旋转过来的节点的右子树上
其次。如果没有，因为开头说过，所有节点的空节点，都指向了我们自己设置的空节点Nul，
所以只需要让p的右子树指向它就好了。*/
if (s->_rightChild != Nul)
s->_rightChild->_parent = p;
p->_leftChild = s->_rightChild;
s->_parent = p->_parent;
if (p->_parent == Nul) //被旋转的节点是根节点
t = s;
else if (p == p->_parent->_leftChild) //不是根节点，判断是左子树还是右子树进行连接
p->_parent->_leftChild = s;
else
p->_parent->_rightChild = s;
s->_rightChild = p; //将节点的其他指针调整指向
p->_parent = s;
}
为什么这次不同于AVL树使用引用传需要被旋转的值呢，从代码可以知道，这次直接在旋转的同时完成了连接，具体步骤的意义会标识在代码中，这样看着比较方便。
2.左单旋
void RBTree<Type>::RotateL(RBTreeNode<Type>*& t, RBTreeNode<Type>* p)
{
RBTreeNode<Type>* s = p->_rightChild;
/*判断即将要旋转的位置是否有左子树，有的话就将其挂在未来旋转过来的节点的右子树上
其次。如果没有，因为开头说过，所有节点的空节点，都指向了我们自己设置的空节点Nul，
所以只需要让p的右子树指向它就好了。*/
if (s->_leftChild != Nul)
s->_leftChild->_parent = p;
p->_rightChild = s->_leftChild;
s->_parent = p->_parent;
if (p->_parent == Nul) //被旋转的节点是根节点
t = s;
else if (p == p->_parent->_leftChild) //不是根节点，判断是左子树还是右子树进行连接
p->_parent->_leftChild = s;
else
p->_parent->_rightChild = s;
s->_leftChild = p; //将节点的其他指针调整指向
p->_parent = s;
}
四、红黑树的插入
template<typename Type>
void RBTree<Type>::_Insert(RBTreeNode<Type>* &t, const Type val)
{
RBTreeNode<Type>* p = t;
RBTreeNode<Type>* pr = Nul;
while (p != Nul) //寻找插入位置
{
if (val == p->_Val) //不接受相同数据
return;
pr = p;
if (val > p->_Val)
p = p->_rightChild;
else
p = p->_leftChild;
}
p = _BuyNode(val);
if (pr == Nul) // 插入的是第一个根节点
{
t = p;
t->_parent = pr;
}
if (val > pr->_Val)
pr->_rightChild = p;
else
pr->_leftChild = p;
p->_parent = pr;
/*调整平衡*/
In_balance(t, p);
}
template<typename Type>
void RBTree<Type>::In_balance(RBTreeNode<Type>*& t, RBTreeNode<Type>*& m)
{
while (m->_parent->_color == RED)
{
RBTreeNode<Type>* u; //uncle节点
if (m->_parent == m->_parent->_parent->_leftChild) //左分支
{
u = m->_parent->_parent->_rightChild;
if (u->_color == RED) //状况三 uncle为红色节点
{
m->_parent->_color = BLACK;
m->_parent->_parent->_color = RED;
u->_color = BLACK;
m = m->_parent->_parent;
}
else //uncle为黑色节点
{
if (m == m->_parent->_rightChild) //状况二
{
m = m->_parent;
RotateL(t, m);
}
m->_parent->_color = BLACK; //状况一
m->_parent->_parent->_color = RED;
RotateR(t, m->_parent->_parent);
}
}
else //右分支
{
u = m->_parent->_parent->_leftChild;
if (u->_color == RED) //uncle为红色节点
{
//状况三
m->_parent->_color = BLACK;
m->_parent->_parent->_color = RED;
u->_color = BLACK;
m = m->_parent->_parent;
}
else //uncle为黑色节点
{
if (m == m->_parent->_leftChild) //状况二
{
m = m->_parent;
RotateR(t, m);
}
m->_parent->_color = BLACK; //状况一
m->_parent->_parent->_color = RED;
RotateL(t, m->_parent->_parent);
}
}
}
t->_color = BLACK; //不管如何调整，根节点一定是黑色
}
寻找插入位置就不多说了，仔细看一下就会了，主要说一下调整平衡这里：
调整平衡的两种情况
一、uncle节点为黑色
uncle可能存在也可能不存在，无所谓，不存在的话在我们设置的时候也是指向我们自己设置的黑色空节点Nul
情况一 插入节点在外侧插入（单旋转）
我们只需要先将其父节点改为黑色，祖父节点改为红色，在进行单旋转即可达到平衡
情况二 插入节点在内侧插入（双旋转）
先将其进行一次单旋转，使其变成情况一，再通过情况一着色，旋转，达到平衡，这里有一个小细节，就是我们需要提前将m节点追到m的父节点，因为我们的目标就是要让其成为情况一，仔细看过旋转函数的同学一定都发现了，旋转完之后父节点会转下去，所以我们需要根据旋转函数体现追到父节点，使其旋转过后成为情况一
二、uncle节点为红色
这时我们的处理比较简单，我们只需要将其father节点和uncle节点的颜色改为黑色，grandfather节点的颜色改为红色，然后继续向上调整即可，这时又会转换成上面的情况一或者情况二，再根据相应的调整方式进行调整即可
五、红黑树的删除
template<class Type>
void RBTree<Type>::_Remove(RBTreeNode<Type>*& t, const Type val)
{
RBTreeNode<Type>* p = t;
while (p != Nul) //寻找要被删除的节点
{
if (p->_Val == val)
break;
if (val > p->_Val)
p = p->_rightChild;
else
p = p->_leftChild;
}
RBTreeNode<Type>* q;
if (p == Nul) //被删除节点不存在
return;
if (p->_leftChild != Nul && p->_rightChild != Nul) //被删除节点有左右子树
{
q = p->_leftChild;
while (q->_rightChild != Nul)
q = q->_rightChild;
p->_Val = q->_Val;
p = q;
}
if (p->_leftChild != Nul) //被删除节点只有一个子树
q = p->_leftChild;
else
q = p->_rightChild;
q->_parent = p->_parent; //将q节点挂到被删除的节点的父节点的子树上
if (q->_parent == Nul) // 被删除的是根节点
{
t = q;
t->_color = BLACK;
delete p;
return;
}
if (p == p->_parent->_leftChild) //父节点在对应的左树或者右树连接p的子树
p->_parent->_leftChild = q;
else
p->_parent->_rightChild = q;
/*调整平衡*/
if (p->_color == BLACK)
{
if (q != Nul) //组合四: 直接互换颜色，删除p节点即可
q->_color = BLACK;
else //组合二
Re_balance(t, q);
}
delete p;
}
template<class Type>
void RBTree<Type>::Re_balance(RBTreeNode<Type>*& t, RBTreeNode<Type>*& m)
{
while (m != t)
{
RBTreeNode<Type>* b;
if (m == m->_parent->_leftChild) //左分支
{
b = m->_parent->_rightChild;
/*——— 情形四 ———*/
if (b->_color == RED)
{
b->_color = BLACK;
m->_parent->_color = RED;
RotateL(t, m->_parent);
b = m->_parent->_rightChild;
}
/*——— 情形三 ———*/
if (b->_leftChild->_color != RED && b->_rightChild->_color != RED)
{
b->_color = RED;
if (m->_parent->_color == RED)
{
m->_parent->_color = BLACK;
m = t;
}
else
m = m->_parent; //向上回溯，继续判断
}
else
{
/*——— 情形二 ———*/
if (b->_leftChild->_color == RED)
{
b->_color = RED;
b->_leftChild->_color = BLACK;
RotateR(t, b);
b = b->_parent;
}
/*——— 情形一 ———*/
b->_color = m->_parent->_color;
m->_parent->_color = BLACK;
b->_rightChild->_color = BLACK;
RotateL(t, m->_parent);
m = t;
}
}
else //右分支
{
b = m->_parent->_leftChild;
/*——— 情形四 ———*/
if (b->_color == RED)
{
b->_color = BLACK;
m->_parent->_color = RED;
RotateR(t, m->_parent);
m = m->_parent;
}
/*——— 情形三 ———*/
if (b->_leftChild->_color != RED && b->_rightChild->_color != RED)
{
b->_color = RED;
if (m->_parent->_color = RED)
{
m->_parent->_color = BLACK;
m = t;
}
else
m = m->_parent;
}
else
{
/*——— 情形二 ———*/
if (b->_rightChild->_color == RED)
{
b->_color = RED;
b->_rightChild->_color = BLACK;
RotateL(t, b);
b = b->_parent;
}
/*——— 情形一 ———*/
b->_color = m->_parent->_color;
m->_parent->_color = BLACK;
b->_leftChild->_color = BLACK;
RotateR(t, m->_parent);
m = t;
}
}
t->_color = BLACK;
}
}
如何寻找删除位置以及，被删除节点的子节点的处理，跟AVL树相同，都将其化成至多只有一个子树 或者 没有子树的情况，所以这里就不在多说，主要说一下，删除时，不同颜色，不同位置的节点，如何进行删除。
删除时会遇到的六种情况
情况一：
删除节点为RED节点，并且为叶子节点，那么直接删除即可
情况二：
删除节点为RED节点，只有一个叶子节点
解释：
这种情况是不存在的，不然会导致其违背红黑树的性质——每条路径上的黑色节点数目相同；又或者违背红黑树的性质——红色节点不能相连
情况三：
删除节点为BLACK节点，只有一个叶子节点
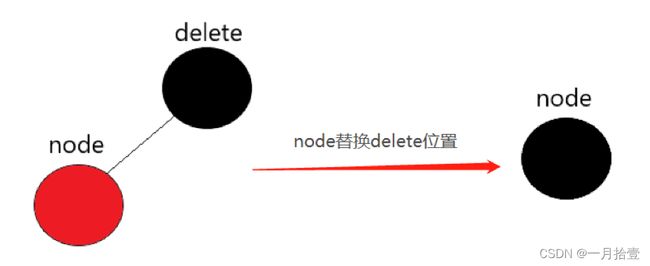
解释：
该节点的叶子节点颜色只能为RED，如果是BLACK节点，还是会违背红黑树的性质——每条路径上的黑色节点数目相同，所以，只能是RED叶子节点，那么直接将叶子节点颜色改为BLACK,用叶子节点代替被删除节点的位置，即可达到平衡
情况四、五
被删除节点有两个节点，这里被删除节点可能为RED或者BLACK
解释：
这里的替换寻找都与AVL树相同，这里节点颜色不一定就是这个样子，只是举例而已，所以不在多说，替换之后，情况四、五将转化成情况三 或者 情况六
情况六
删除节点为BLACK节点，且没有子节点。
这种情况下又有四种情形：
情形一：
被删除节点的brother节点有一个于其方向相同的子节点
解释：
先将father节点和brother节点的颜色互换，然后对father节点进行一次左旋转，然后将mine节点删除，就可以达到平衡。
情形二：
被删除节点的brother节点有一个于其方向相反的子节点
解释：
首先，先将brother节点与son节点颜色互换，然后对brother节点进行一次右旋转，这时，就变成了情形一，再进行情形一的操作，就可以达到平衡
情形三
brother节点没有红色子节点
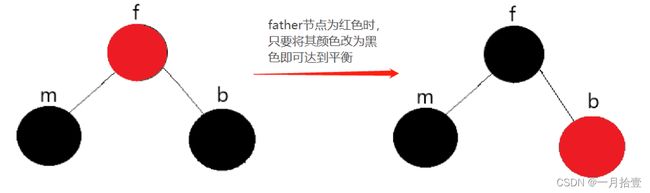
解释：
当father节点为红色时，先将brother颜色改为红色然后将father节点颜色改为黑色，最后将mine节点删除即可达到平衡
解释：
这里细心的小伙伴可以看到，father节点从圆形变成了黑色，这里叫做“双重黑色”，它是我们假定的黑色，它并不是真实存在的，而是我们自己主观的想象，这种情况的出现是mine节点将自己的黑色给了father节点，这样我们就当作它平衡了，它黑色减少了，但是father本来就是黑色，然后现在有多了一重，所以是双重黑色，那么理所当然，我们需要删掉这个多余的黑色，所以需要将brother节点颜色改为红色然后继续向上回溯，继续调整平衡。
情况四
brother节点为红色
解释：
先将father和brother节点的颜色进行调整，然后对father节点进行左旋，这时，新的brother节点就是son节点，这就转化成brother节点为BLACK的情况，这样就可以转化成上面其他几种情况来进行响应的调整。
六、源代码
#include